조합(Combination) 구하기

개요

• 입력 크기($N$)와 문제 조건(모듈러 연산 여부)에 따라 적절한 알고리즘 선택이 필요함
• 조합을 구하는 3가지 방법(팩토리얼, DP, 페르마의 소정리)을 비교하고 수학적 원리를 설명함

조합의 정의

• 서로 다른 $n$개 중에서 순서에 상관없이 $r$개를 선택하는 경우의 수임
• 수학적 정의

\[_nC_r = \frac{n!}{r!(n-r)!}\]

방법 1 - 단순 팩토리얼 계산

접근 방식

• 수학 공식을 코드로 직접 구현함
• 분자($n!$)를 계산한 후 분모($r!(n-r)!$)로 나눔

한계점

• 오버플로우 발생 위험
  • $20!$ 이상의 계산 시 long 타입 범위를 초과함
  • 숫자가 커질 경우 정확한 결과 도출이 불가능함
• 부동소수점 오차 발생 가능성
  • 나눗셈 연산을 위해 double 타입을 사용할 경우 정밀도 문제가 발생함

방법 2 - 동적 계획법 (Dynamic Programming)

파스칼의 법칙 이용

• 팩토리얼 계산 없이 덧셈 연산만으로 조합을 구하는 방식임
• 입력 크기 $N$이 작을 때(약 2,000 이하) 주로 활용함

수학적 원리 및 증명

• 점화식 성립

\[_nC_r = _{n-1}C_{r-1} + _{n-1}C_r\]

• 증명 논리

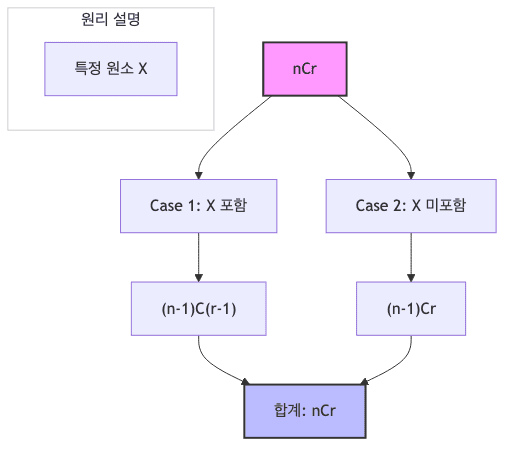
  • $n$개의 원소 중 특정한 원소 $X$를 기준으로 사건을 분류함
  • Case 1 ($X$ 포함)
    • 남은 $n-1$개 중 $r-1$개를 선택함
  • Case 2 ($X$ 미포함)
    • 남은 $n-1$개 중 $r$개를 선택함
  • 두 사건은 배반 사건이므로 합의 법칙 적용이 가능함

  

코드 구현 (Java)

• 2차원 배열을 이용한 메모이제이션 적용

  int[][] D = new int[n + 1][n + 1];
  
  for (int i = 0; i <= n; i++) {
      D[i][0] = 1; // n개 중 0개 선택
      D[i][i] = 1; // n개 중 n개 선택
      D[i][1] = i; // n개 중 1개 선택
      for (int j = 2; j < i; j++) {
          // 점화식 적용 (필요 시 모듈러 연산 추가)
          D[i][j] = D[i - 1][j - 1] + D[i - 1][j];
      }
  }
  

특징 및 분석

• 장점
  • 나눗셈 연산이 없어 구현이 단순함
  • 모듈러 연산 적용이 용이함
• 단점
  • $O(N^2)$의 시간 및 공간 복잡도 발생함
  • $N$이 10,000을 초과할 경우 메모리 부족 위험 존재함

방법 3 - 페르마의 소정리

아이디어

• 입력 크기 $N$이 매우 클 때($1,000,000$ 이상) 사용 가능한 효율적인 방식임
• 분모의 나눗셈 연산을 곱셈 연산으로 변환하여 모듈러 분배 법칙을 적용함

수학적 원리

• 문제 상황 정의
  • 모듈러 연산은 나눗셈에 대해 분배 법칙이 성립하지 않음
  • 분모의 역원을 구하여 곱셈으로 치환해야 함
• 페르마의 소정리 정의
  • $P$가 소수이고 $A$가 $P$의 배수가 아닐 때 다음 식이 성립함
  • \[A^{P-1} \equiv 1 \% P\]
  • 참고
    • 조합 계산에서 $P$는 매우 큰 소수이므로 분모인 $r!$이나 $(n-r)!$이 $P$의 배수가 될 확률은 사실상 0임
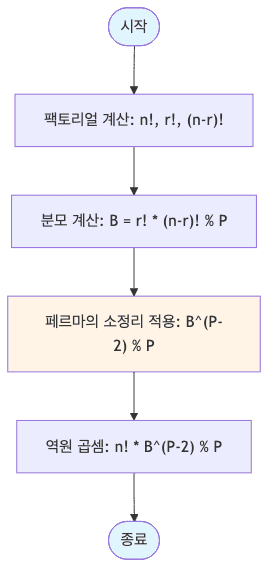
• 역원 유도 및 결론
  • 양변에 $A^{-1}$을 곱하면 $A^{P-2} \equiv A^{-1} \% P$ 가 도출됨
  • 즉, $B$로 나누는 연산은 $B^{P-2}$를 곱하는 연산과 동일함

코드 구현 (Java)

• 거듭제곱을 빠르게 계산하는 분할 정복 알고리즘 활용

  public class CombinationFermat {
      static final int P = 1000000007;
  
      public static void main(String[] args) {
          int N = 100000, R = 40000;
          System.out.println(nCr(N, R));
      }
  
      static long nCr(int n, int r) {
          if (r == 0 || n == r) return 1;
  
          long[] fact = new long[n + 1];
          fact[0] = 1;
  
          // 1. 팩토리얼 사전 계산 (O(N))
          for (int i = 1; i <= n; i++) {
              fact[i] = (fact[i - 1] * i) % P;
          }
  
          // 2. 분모(r! * (n-r)!) 계산
          long bottom = (fact[r] * fact[n - r]) % P;
  
          // 3. 페르마의 소정리로 역원 도출 (bottom^(P-2))
          long inverseBottom = power(bottom, P - 2);
  
          // 4. 최종 결과 산출
          return (fact[n] * inverseBottom) % P;
      }
  
      static long power(long base, long expo) {
          long result = 1;
          while (expo > 0) {
              if (expo % 2 == 1) {
                  result = (result * base) % P; // long 연산을 통한 오버플로우 방지
              }
              base = (base * base) % P; // 오버플로우 발생 전 모듈러 연산 수행
              expo /= 2;
          }
          return result;
      }
  }
  

특징 및 분석

• 장점
  • $O(N + \log P)$의 성능을 제공함
  • 대규모 입력 데이터 처리에 최적화됨
• 단점
  • 모듈러 값이 소수(Prime Number)인 조건에서만 사용 가능함
  • 구현 복잡도가 상대적으로 높음

방법 4 - $_nC_2$ 공식 활용

아이디어

• 조합에서 $r$이 2로 고정된 경우 복잡한 로직 없이 단순 수식으로 계산함
• ‘나머지 합’ 문제처럼 동일한 그룹(나머지 값) 내에서 2개의 인덱스를 선택할 때 주로 사용함

수학적 도출

• $_nC_2$ 공식의 단순화 과정임
• \[_nC_2 = \frac{n!}{2!(n-2)!} = \frac{n \times (n-1)}{2}\]
• 주의
  • 구현 시 정확도를 위해 곱셈($n \times (n-1)$)을 먼저 수행한 후 나눗셈을 실행해야 함

특징 및 장점

• 성능
  • 연산 횟수가 $O(1)$로 사실상 즉시 결과 도출됨
• 구현
  • 별도의 함수나 배열 없이 한 줄의 코드로 구현 가능함
• 주의사항
  • $n$이 클 경우 $n \times (n-1)$ 과정에서 오버플로우가 발생할 수 있으므로 long 타입을 사용해야 함

요약 및 선택 가이드

• 상황에 따라 적절한 알고리즘을 선택해야 함

방법	시간 복잡도	사용 조건	비고
단순 팩토리얼	$O(N)$	$N$이 매우 작을 때	값이 작을 때만 사용 가능함
동적 계획법	$O(N^2)$	$N \le 2,000$	모듈러 연산이 소수가 아닐 때 유용함
페르마의 소정리	$O(N)$	대규모 입력 및 소수 모듈러	대규모 정답 도출의 정석임
$_nC_2$ 공식	$O(1)$	2개를 뽑는 경우	누적 합/쌍 찾기 문제 필수임

Reference

• Do it! 알고리즘 코딩 테스트 - 자바 편