개요
- 구간 합(Prefix Sum)과 합 배열은 배열의 특정 구간 합을 효율적으로 계산하기 위한 알고리즘 기법임
- 데이터가 많을 때 매번 반복문으로 합을 구하면 비효율적이므로, 미리 누적 합을 계산해두고 $O(1)$에 조회하는 방식임
개념
구간 합 (Prefix Sum)
- 배열의 특정 범위(i부터 j까지)에 속한 원소들의 합을 의미함
- 부분합과는 다르게 임의의 구간에 대한 합을 빠르게 구할 수 있음
합 배열 (Sum Array)
- 원본 배열의 0번 인덱스부터 특정 인덱스까지의 누적 합을 저장한 배열임
- 원본 배열을 $A$, 합 배열을 $S$라고 할 때 다음과 같이 정의함
- 1-인덱싱을 사용하면 구현이 더 직관적이므로, $S[0]=0$으로 초기화하고 1부터 사용하는 경우가 많음
예시
-
배열 $A$와 합 배열 $S$의 관계를 숫자로 표현함
인덱스 0 1 2 3 4 5 배열 A 15 13 10 7 3 12 합 배열 S 15 28 38 45 48 60
합 배열 생성 및 계산
합 배열 생성 공식
- 합 배열은 이전 인덱스까지의 누적 합에 현재 원소 값을 더하여 생성함
- $O(N)$의 시간 복잡도로 미리 계산해두면 이후 모든 쿼리를 빠르게 처리 가능함
구간 합 계산 공식
- $i$부터 $j$까지의 구간 합은 합 배열의 뺄셈 연산 한 번으로 구할 수 있음
- $A[2]$부터 $A[5]$까지의 합을 구하는 과정을 예로 듦
-
계산 상세
- $S[5] = 60$ ($A[0]$부터 $A[5]$까지의 합)
- $S[1] = 28$ ($A[0]$부터 $A[1]$까지의 합)
- $60 - 28 = 32$
- 실제 합: $10 + 7 + 3 + 12 = 32$ (일치함)
-
$S[j]$에서 $S[i-1]$을 빼면 $i$부터 $j$구간의 합만 남는 원리를 이용함
내부 동작 흐름
-
사용자가 구간 합을 요청했을 때 합 배열을 이용해 내부적으로 어떻게 계산되는지 나타냄
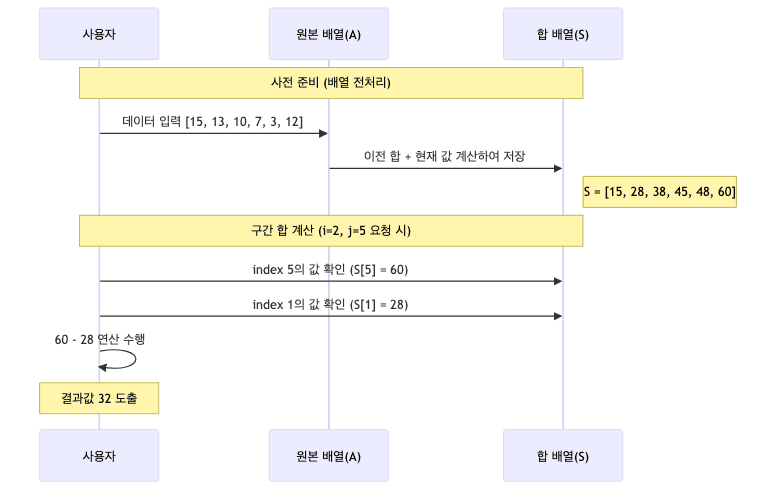
성능 비교
- 구간 합 쿼리가 $M$번 주어졌을 때의 성능 차이는 매우 큼
| 방식 | 합 배열 구성 시간 | 1회 쿼리 시간 | 총 소요 시간 (M회) | 비고 |
|---|---|---|---|---|
| 단순 반복문 | - | $O(N)$ | $O(N \times M)$ | 쿼리가 많으면 시간 초과 발생 |
| 합 배열 | $O(N)$ | $O(1)$ | $O(N + M)$ | 쿼리가 많을수록 압도적으로 유리 |
2차원 구간 합
- 2차원 배열에서도 직사각형 영역의 합을 구하기 위해 확장된 공식을 사용함
- $D[i][j]$를 $(0,0)$부터 $(i,j)$까지의 사각형 영역 합이라고 정의함
2차원 합 배열 생성
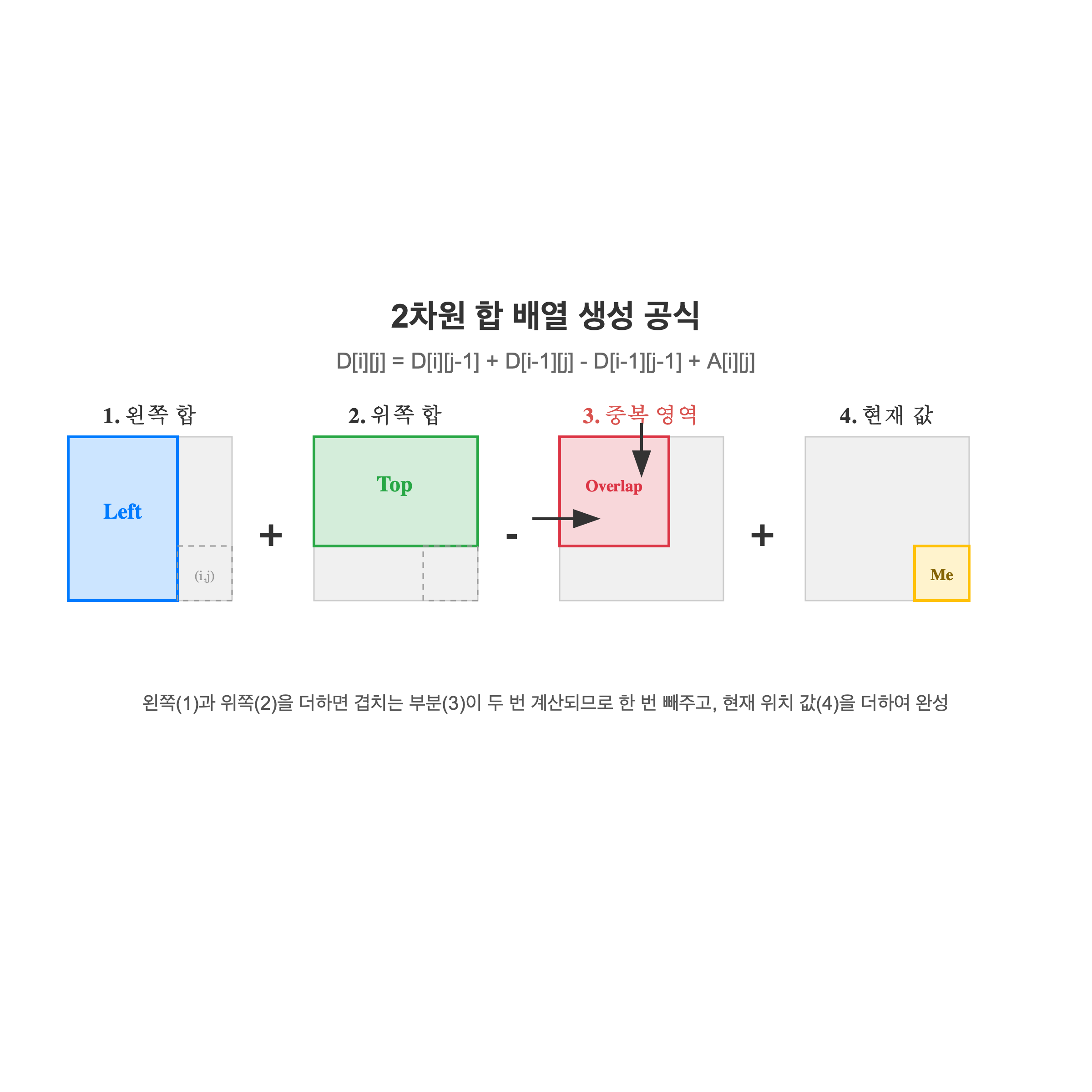
\[D[i][j] = D[i-1][j] + D[i][j-1] - D[i-1][j-1] + A[i][j]\]- 2차원 합 배열의 각 칸은 원본 배열의 $(0, 0)$부터 현재 위치 $(i, j)$까지 이루는 사각형 영역의 모든 숫자 합을 의미함
- 공식은 사각형의 면적을 채워 나가는 과정과 같음
수식의 구성 요소
- 왼쪽 영역 더하기 ($D[i][j-1]$)
- 현재 칸을 기준으로 왼쪽 끝까지의 모든 합을 먼저 가져옴
- 위쪽 영역 더하기 ($D[i-1][j]$)
- 현재 칸을 기준으로 위쪽 끝까지의 모든 합을 추가로 더함
- 중복 영역 빼기 ($- D[i-1][j-1]$)
- 왼쪽 영역과 위쪽 영역을 각각 더할 때 왼쪽 위 대각선 영역이 두 번 포함되는 문제가 발생함
- 정확한 합을 계산하기 위해 두 번 더해진 대각선 영역을 한 번 빼줌
-
현재 값 더하기 ($+ A[i][j]$)
-
마지막으로 현재 좌표에 해당하는 원본 배열의 값을 더해주면 $(i, j)$까지의 사각형 합이 완성됨
-
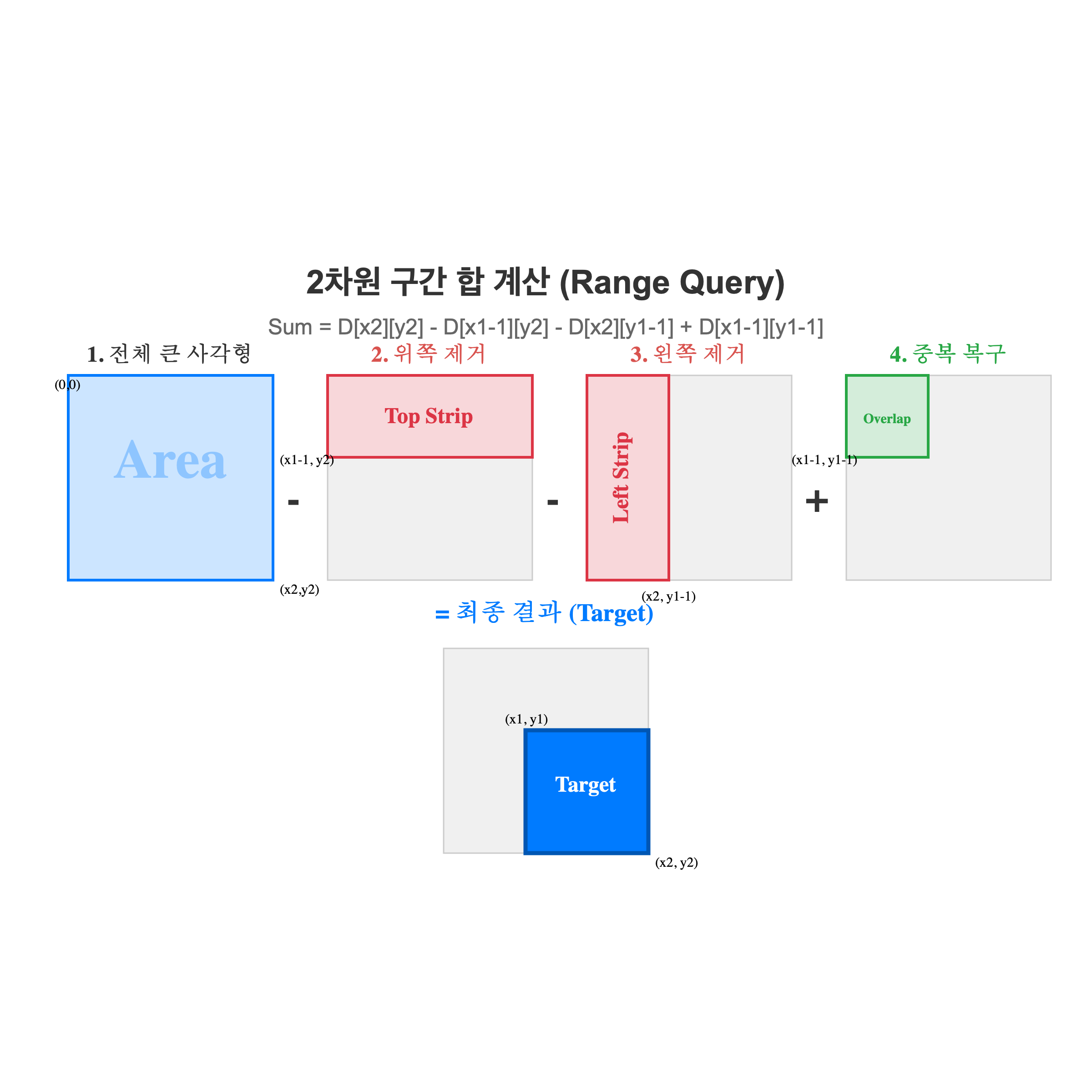
2차원 구간 합 계산
- $(x1, y1)$부터 $(x2, y2)$까지의 사각형 영역 합을 구하는 공식
-
전체 큰 사각형에서 필요 없는 위쪽과 왼쪽 영역을 빼고, 두 번 빠진 왼쪽 위 대각선 영역을 다시 더해줌 (포함-배제 원리)
Java 구현 코드
1차원 구간 합
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class PrefixSumExample {
public static void main(String[] args) {
int[] arr = {15, 13, 10, 7, 3, 12};
int[] sum = new int[arr.length + 1]; // 1-Based Indexing (크기 N+1)
// 합 배열 구성: O(N)
// S[0] = 0 (자동 초기화)으로 두고 1부터 채움
for (int i = 1; i <= arr.length; i++) {
sum[i] = sum[i - 1] + arr[i - 1];
}
// 구간 합 계산 (예: 3번째 ~ 6번째 원소, 즉 A[2]~A[5])
// 1-Based Indexing 기준이므로 i=3, j=6
int i = 3, j = 6;
// 공식: S[j] - S[i-1]
// 1-Based를 사용하면 i=1일 때 S[0]이 0이므로 별도 예외 처리가 필요 없음
int result = sum[j] - sum[i - 1];
System.out.println("Result: " + result);
}
}
2차원 구간 합
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public class PrefixSum2DExample {
public static void main(String[] args) {
int[][] arr = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
int n = arr.length;
int m = arr[0].length;
int[][] sum = new int[n + 1][m + 1];
// 2차원 합 배열 구성: O(N*M)
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
sum[i][j] = sum[i-1][j] + sum[i][j-1]
- sum[i-1][j-1] + arr[i-1][j-1];
}
}
// 구간 합 계산 (예: (1,1) ~ (3,3)): O(1)
int x1 = 1, y1 = 1, x2 = 3, y2 = 3;
int result = sum[x2][y2] - sum[x1-1][y2]
- sum[x2][y1-1] + sum[x1-1][y1-1];
System.out.println("Result: " + result);
}
}