나머지 연산과 구간 합

개요

• 알고리즘에서 구간 합(Prefix Sum)은 $O(N)$의 전처리를 통해 $O(1)$로 구간의 합을 구하는 도구임
• 여기에 나머지 연산(Modular Arithmetic)의 분배 법칙을 결합하면 복잡한 연산 과정을 줄이는 최적화가 가능함
• 이 글에서는 두 개념의 수학적 증명과 이를 통해 도출되는 동치 관계를 설명함

나머지 연산의 성질

덧셈과 뺄셈의 분배 법칙

• 나머지 연산은 덧셈과 뺄셈에 대해 분배 법칙이 성립하며 연산의 순서를 바꾸어도 결과가 동일함

• 정의

  \((A + B) \% M = ((A \% M) + (B \% M)) \% M\) \((A - B) \% M = ((A \% M) - (B \% M)) \% M\)

• 의미
  • 거대한 수 $A$, $B$를 직접 더하거나 뺀 후 나머지를 구하는 것과 각각의 나머지를 먼저 구한 후 연산하는 것은 같음
  • 이는 오버플로우(Overflow)를 방지하고 연산 효율을 높이는 핵심 원리가 됨

구간 합의 재해석

구간 합의 정의

• 수열 $A$가 있을 때 $S[i]$는 0번째부터 $i$번째 원소까지의 누적 합을 의미함

\[S[i] = A[0] + A[1] + \dots + A[i]\]

차분을 이용한 구간 합

• 원본 수열의 $i$번째부터 $j$번째까지의 부분 합은 두 누적 합의 차로 표현됨

\[Sum(i, j) = S[j] - S[i-1]\]

• 결론
  • 구간의 합이라는 복잡한 연산이 두 수의 뺄셈이라는 단순 연산으로 치환됨

수학적 증명

• 구간 합이 특정 수 M으로 나누어떨어지는지 확인하는 문제에서 다음과 같은 수학적 성질이 성립함
• 이 성질을 이용하면 $O(N^2)$의 구간 합 계산 문제를 단순한 카운팅 문제로 치환할 수 있음

문제의 수식화

• 구간 합 $Sum(i, j)$가 $M$으로 나누어떨어진다는 것은 나머지가 0이라는 의미임

\[(S[j] - S[i-1]) \% M = 0\]

모듈러 연산 성질 적용

• 모듈러 뺄셈의 성질에 의해 위 식은 다음과 같이 변형됨

\[S[j] \% M - S[i-1] \% M = 0\]

• 이를 우변으로 이항하면 다음과 같은 합동식이 성립함

\[S[j] \% M = S[i-1] \% M\]

증명 결과

• 나머지가 같은 두 인덱스 $i$, $j$가 존재한다면 ($i < j$이며 $S[i] \% M = S[j] \% M$), 원본 배열의 $(i+1)$번째부터 $j$번째까지의 합은 반드시 $M$의 배수임
• 이 증명 덕분에 복잡한 구간 합을 계산할 필요 없이 나머지가 같은 인덱스가 몇 개 있는지만 세면 됨

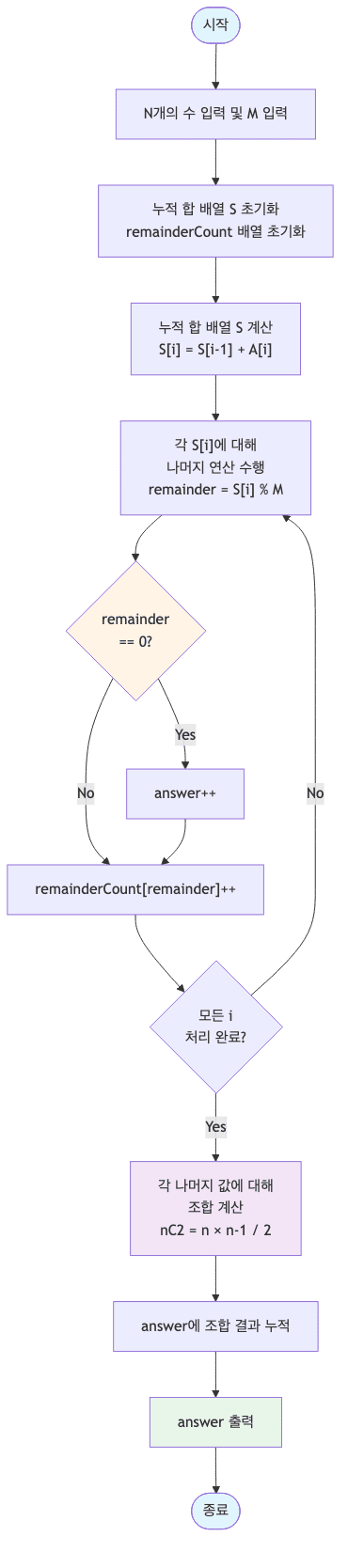
예시로 보는 동작 원리

• 실제 숫자를 대입하여 알고리즘이 어떻게 동작하는지 확인함
• 입력
  • 배열 A = [1, 2, 3, 1, 2]
  • 나누는 수 M = 3

누적 합(S) 계산

• $S[0] = 1$
• $S[1] = 1 + 2 = 3$
• $S[2] = 3 + 3 = 6$
• $S[3] = 6 + 1 = 7$
• $S[4] = 7 + 2 = 9$
• 결과
  • S = [1, 3, 6, 7, 9]

나머지 연산(S % M) 수행

• $1 \% 3 = 1$
• $3 \% 3 = 0$
• $6 \% 3 = 0$
• $7 \% 3 = 1$
• $9 \% 3 = 0$
• 결과
  • Remainder = [1, 0, 0, 1, 0]

정답 카운팅

• 나머지가 0인 경우
  • 누적 합 자체가 0으로 나누어떨어지므로 처음(인덱스 0)부터 해당 위치까지의 합이 M의 배수를 의미함
  • 인덱스 1, 2, 4 (총 3개)
  • +3
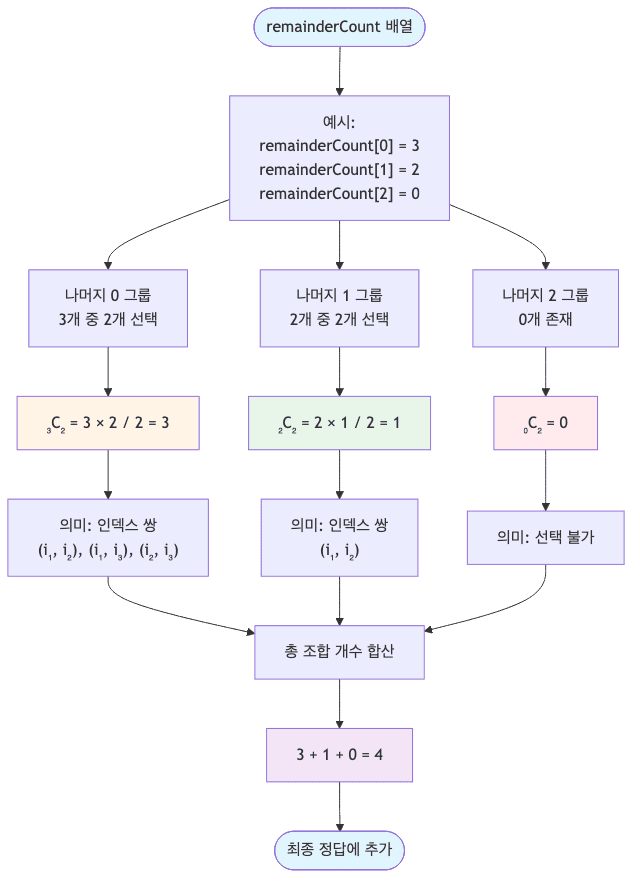
• 나머지가 같은 인덱스끼리의 조합
  • 나머지 0인 인덱스(1, 2, 4) 중 2개 선택
    • $_3C_2 = 3$
    • +3
  • 나머지 1인 인덱스(0, 3) 중 2개 선택
    • $_2C_2 = 1$
    • +1
• 최종 정답
  • $3 + 3 + 1 = 7$

알고리즘적 응용 및 주의사항

최적화 효과

• 기존 방식 ($O(N^2)$)
  • 모든 구간을 일일이 더해보고 확인해야 함
  • $N=10^5$일 때 시간 초과 발생
• 최적화 방식 ($O(N)$)
  • 배열을 한 번만 순회하며 나머지를 카운팅하고 조합 공식으로 즉시 정답 도출

주의사항 - 데이터 타입 (Overflow)

• $N$이 크고 수열의 원소가 크다면 누적 합은 int 범위를 쉽게 초과함
• 반드시 long 타입을 사용해야 오버플로우를 방지할 수 있음

주의사항 - 음수 나머지 (Negative Modulo)

• Java나 C++에서 음수를 양수로 나눌 경우 음수 나머지가 반환될 수 있음
  • 예시: -5 % 3 = -2
• 수학적으로 나머지는 항상 $0$ 이상이어야 하므로 보정 코드가 필요함

• int remainder = (S[i] % M);
  // Java의 % 연산자는 음수일 경우 음수를 반환하므로 보정 필요
  if (remainder < 0) remainder += M;
  

요약

• 나머지 연산의 분배 법칙 덕분에 구간 합의 나머지 연산을 분리할 수 있음
• 구간 합의 차분 성질과 결합하여 $S[j] \% M = S[i] \% M$ 이면 구간 합은 $M$의 배수이다라는 수학적 증명이 성립함
• 이를 통해 복잡한 구간 합 문제를 단순한 카운팅 및 조합($_nC_2$) 문제로 치환하여 $O(N)$에 해결할 수 있음

Reference

• Do it! 알고리즘 코딩 테스트 - 자바 편