투 포인터 알고리즘

개요

• 투 포인터(Two Pointers)는 1차원 배열에서 두 개의 포인터를 조작하여 원하는 결과를 얻는 알고리즘 기법임
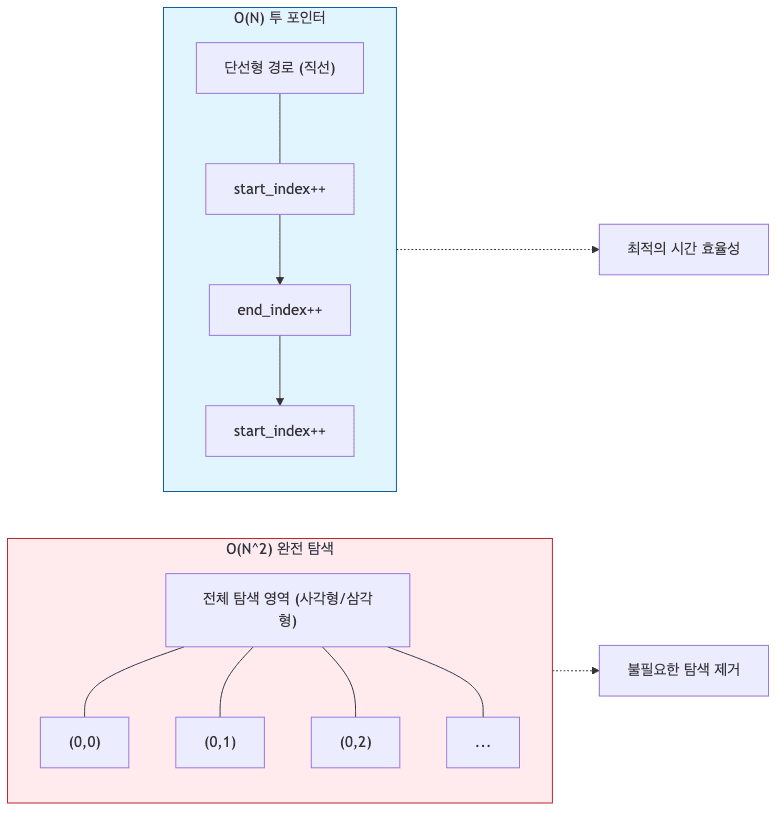
• 완전 탐색 적용 시 $O(N^2)$이 소요되는 문제를 $O(N)$으로 최적화할 때 활용함
• 연속된 구간의 합을 구하거나 정렬된 배열에서 특정 조건을 만족하는 쌍을 찾는 문제에 효과적임

투 포인터의 필요성

완전 탐색의 한계

• $N$개의 데이터에서 조건을 만족하는 부분 배열을 찾기 위해 이중 반복문을 사용할 경우 비효율이 발생함
• $N=100,000$일 때 $O(N^2)$ 연산량은 약 100억 번에 달하여 시간 초과(Time Limit Exceeded)를 유발함

투 포인터의 해결 방식

• 두 개의 포인터(start, end)를 사용하여 배열을 한 번만 순회하는 선형 탐색을 수행함
• 포인터 이동 규칙을 설정하여 불필요한 연산을 건너뛰고 효율성을 확보함

투 포인터 이동 원칙

• 문제 유형에 따라 포인터의 이동 원칙이 상이함
• ‘연속 구간 합’을 구하는 방식과 ‘정렬된 배열에서 두 수의 합’을 구하는 방식으로 구분됨

같은 방향 패턴 (Sliding Window 스타일)

• 연속된 부분 수열의 합을 구할 때 사용하며 현재 합(sum)과 목표값(target)을 비교함
• sum > target
  • 현재 합이 크므로 범위를 좁히기 위해 start_index를 오른쪽으로 이동 시킴 (start_index++)
• sum < target
  • 현재 합이 작으므로 범위를 넓히기 위해 end_index를 오른쪽으로 이동 시킴 (end_index++)
• sum == target
  • 조건을 만족하므로 카운트를 증가 시키고 end_index를 확장 시킴

반대 방향 패턴 (Converging 스타일)

• 정렬된 배열에서 두 수의 합을 구할 때 사용하며 양쪽 끝 포인터(i, j)의 합과 목표값(target)을 비교함
• A[i] + A[j] > target
  • 합이 목표보다 크므로 더 작은 값이 필요함
  • 오른쪽 포인터 인덱스를 내림 (j--)
• A[i] + A[j] < target
  • 합이 목표보다 작으므로 더 큰 값이 필요함
  • 왼쪽 포인터 인덱스를 올림 (i++)
• A[i] + A[j] == target
  • 조건을 만족하므로 양쪽 포인터를 모두 이동 시키고 카운트를 증가 시킴(i++, j--, count++)

반대 방향 패턴 (Converging Pointers)

• 포인터가 배열의 양 끝에서 시작하여 중심을 향해 좁혀오는 방식임
• 전제 조건
  • 배열이 반드시 정렬되어 있어야 함
  • 정렬되지 않은 경우 $O(N \log N)$의 정렬 과정을 거친 후 적용함

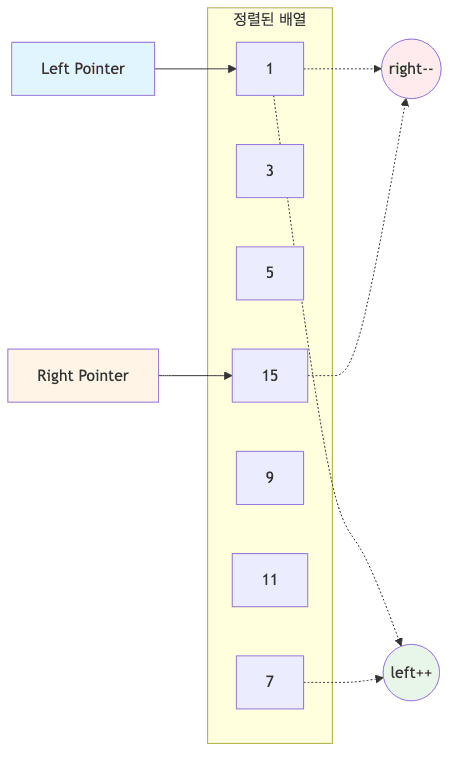
두 수의 합이 목표보다 클 때 (A[i] + A[j] > target)

• 현재 합이 목표보다 크므로 더 작은 값이 필요함
• 오른쪽 끝 포인터 인덱스를 왼쪽으로 이동 시킴 (j--)

두 수의 합이 목표보다 작을 때 (A[i] + A[j] < target)

• 현재 합이 목표보다 작으므로 더 큰 값이 필요함
• 왼쪽 끝 포인터 인덱스를 오른쪽으로 이동 시킴 (i++)

두 수의 합이 목표와 같을 때 (Match)

• 조건을 만족하므로 결과 카운트를 증가 시킴
• i++, j--를 동시에 수행하여 양쪽 포인터를 좁힘

Java 구현 예시 (두 수의 합 찾기)

• 정렬된 배열에서 두 수의 합이 target인 경우를 찾는 로직임

int i = 0;
int j = arr.length - 1;

while (i < j) {
    int sum = arr[i] + arr[j];
    if (sum == target) {
        count++;
        // 중복 데이터 처리를 위한 추가 로직
        while (i < j && arr[i] == arr[i + 1]) i++;
        while (i < j && arr[j] == arr[j - 1]) j--;
        i++;
        j--;
    } else if (sum > target) {
        j--;
    } else {
        i++;
    }
}

중복 데이터 처리 방법

• 같은 숫자가 여러 개 존재할 때 단순히 포인터를 이동하면 누락되는 쌍이 생길 수 있음
• while 문을 사용하여 이전 값과 동일한 인덱스를 건너뛰는 처리가 포함되어야 함

같은 방향 패턴 (Sliding Window Style)

• 두 포인터가 모두 0에서 시작하여 같은 방향으로 이동하는 방식임
• 연속된 수열의 합이나 가변적인 윈도우 크기를 다루는 문제에서 활용됨

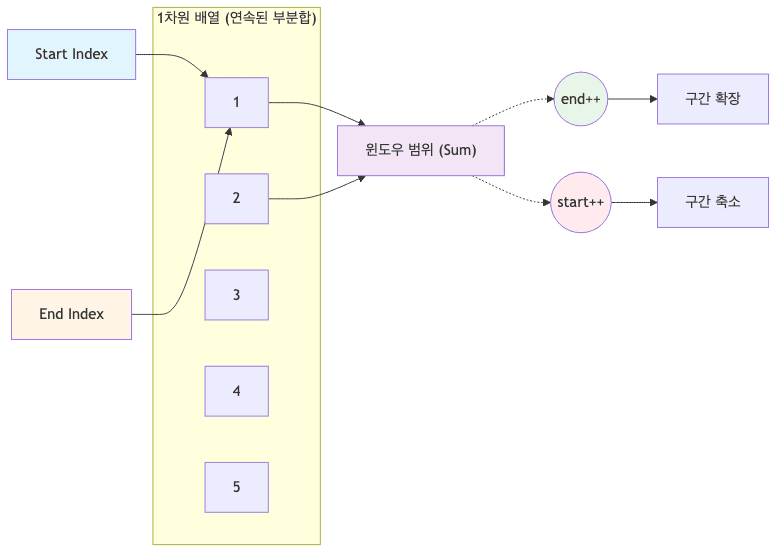
구간 합이 목표보다 클 때 (sum > target)

• 현재 부분 합이 크므로 범위를 축소하여 합을 줄여야 함
• start_index를 오른쪽으로 한 칸 이동 시킴 (start_index++)

구간 합이 목표보다 작을 때 (sum < target)

• 현재 부분 합이 작으므로 범위를 확장하여 합을 키워야 함
• end_index를 오른쪽으로 한 칸 이동 시킴 (end_index++)

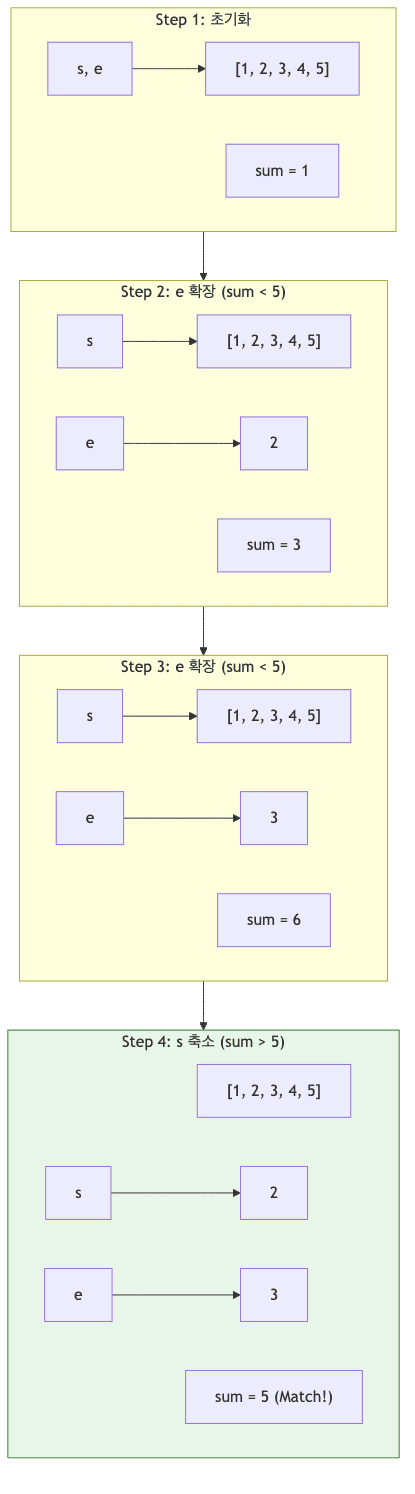
동작 시뮬레이션

• 배열 [1, 2, 3, 4, 5]에서 합이 5인 구간을 찾는 과정임

Java 구현 (연속된 자연수의 합)

• 시작 인덱스가 1인 경우에 대해 합이 target인 구간을 탐색함

int start_index = 1, end_index = 1;
int sum = 1, count = 1;

while (end_index != target) {
    if (sum == target) {
        count++;
        end_index++;
        sum += end_index;
    } else if (sum > target) {
        sum -= start_index;
        start_index++;
    } else {
        end_index++;
        sum += end_index;
    }
}

제약 사항 및 주의점

• 양수 데이터 조건
  • 배열의 원소가 모두 양수일 때 합의 증감이 포인터 이동에 따라 예측 가능해짐
  • 음수가 포함된 경우 start 이동 시 sum이 반드시 줄어든다는 보장이 없어 로직이 성립하지 않음
• 음수 포함 문제 해결
  • 음수가 포함된 구간 합 문제는 누적 합과 해시맵을 결합한 방식을 권장함
  • 상세 내용은 나머지 합 (Prefix Sum with Modular) 포스팅을 참고함

투 포인터 vs 슬라이딩 윈도우

구분	투 포인터 (Two Pointers)	슬라이딩 윈도우 (Sliding Window)
윈도우 크기	가변적임 (조건에 따라 변화)	고정적임 (일정한 크기 유지)
포인터 개수	2개 (독립적 이동 가능)	2개 (일정한 간격 유지)
주요 용도	구간 합, 특정 수 합 찾기	연속된 구간의 최대/최소값

시간 복잡도 증명

• $O(N)$의 시간 복잡도가 유지되는 논리적 근거임
• 포인터 이동 횟수
  • start 포인터 이동 횟수
  • 최대 $N$번
  • end 포인터 이동 횟수
  • 최대 $N$번
• 두 포인터는 각자 독립적으로 한 방향으로만 이동하며 역행하지 않음
• 전체 연산 횟수는 최대 $2N$에 비례하므로 시간 복잡도는 $O(N)$임

알고리즘 적용 가이드

데이터 타입 선택

• 구간의 합을 저장하는 sum 변수는 오버플로우 방지를 위해 long 타입을 기본으로 사용함

인덱스 범위 체크

• while 문 조건에서 end_index가 배열 크기에 도달했을 때의 예외 처리를 철저히 함
• 루프 종료 시 마지막 구간에 대한 누락 여부를 확인함

추천 문제 유형

• 정렬된 배열에서의 두 수의 합 찾기
• 연속된 자연수의 합 구하기
• 부분 배열의 합이 특정 값인 경우 도출하기
• 두 배열의 공통 원소 추출하기

요약 정리

• sum과 target을 비교하여 구간의 확장 및 축소를 결정하는 기법임
• 작을 경우 end를 늘려 합을 키우고, 클 경우 start를 늘려 합을 줄임
• 불필요한 탐색을 제거하여 $O(N^2)$ 문제를 $O(N)$으로 최적화함

Reference

• Do it! 알고리즘 코딩 테스트 - 자바 편