비교 정렬 알고리즘

개요

• 정렬 알고리즘은 데이터를 일정한 순서로 배치하는 알고리즘임
• 비교 정렬은 데이터 간의 상대적 크기 관계를 비교하여 정렬하는 방식임
• 이론적 하한선은 $O(n \log n)$임

비교 정렬이란

• 데이터 간의 대소 관계를 비교하여 정렬 순서를 결정하는 알고리즘임
• 버블, 선택, 삽입, 병합, 퀵, 힙 정렬 등이 포함됨
• 비교 연산을 기반으로 하므로 최소 $O(n \log n)$의 시간 복잡도를 가짐

성능 비교

알고리즘	평균 시간 복잡도	최악 시간 복잡도	최선 시간 복잡도	공간 복잡도	안정성
버블 정렬	$O(n^2)$	$O(n^2)$	$O(n)$	$O(1)$	안정
선택 정렬	$O(n^2)$	$O(n^2)$	$O(n^2)$	$O(1)$	불안정
삽입 정렬	$O(n^2)$	$O(n^2)$	$O(n)$	$O(1)$	안정
병합 정렬	$O(n \log n)$	$O(n \log n)$	$O(n \log n)$	$O(n)$	안정
퀵 정렬	$O(n \log n)$	$O(n^2)$	$O(n \log n)$	$O(\log n)$	불안정
힙 정렬	$O(n \log n)$	$O(n \log n)$	$O(n \log n)$	$O(1)$	불안정

정렬 알고리즘

버블 정렬

• 인접한 두 요소를 비교하여 크기 순서가 맞지 않으면 교환하는 방식임
• 거품이 수면으로 올라오는 것처럼 큰 요소가 배열의 끝으로 이동함

• 구현이 단순하지만 성능이 매우 떨어짐

• 시간 복잡도
  • 평균
    • $O(n^2)$
  • 최악
    • $O(n^2)$
  • 최선
    • $O(n)$
• 공간 복잡도
  • $O(1)$

• 안정성

  • 안정적임

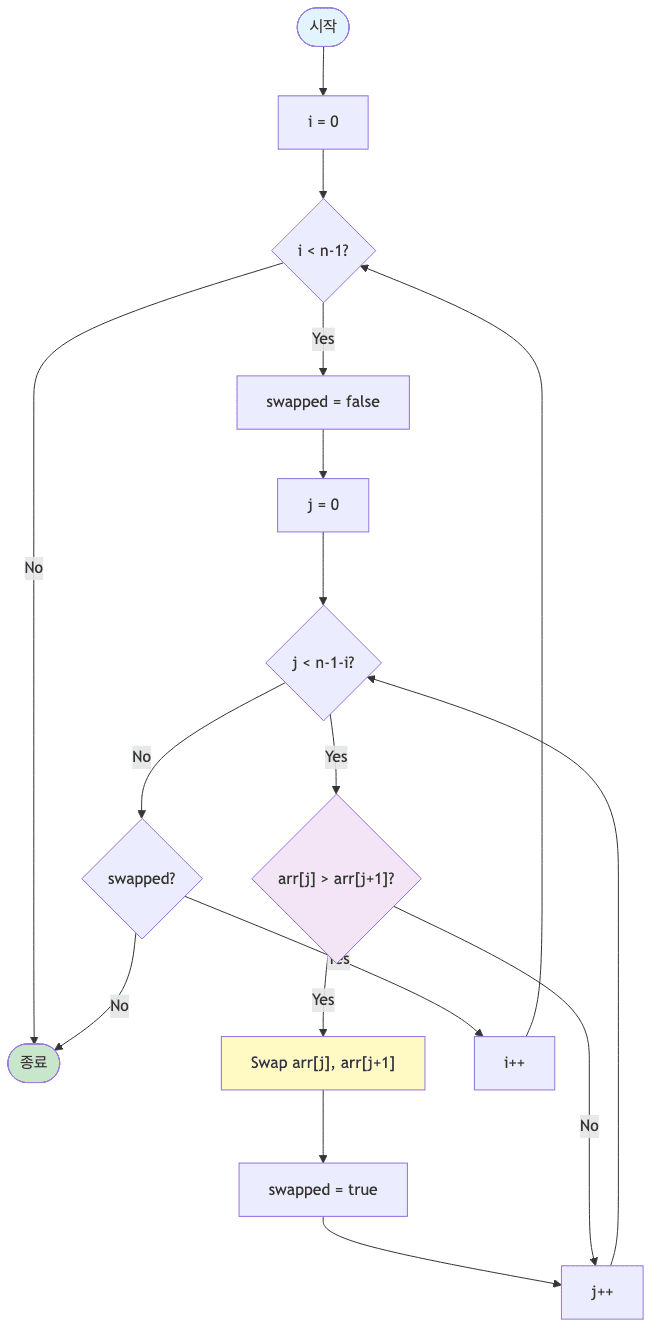
• 과정

  1. 비교 연산이 필요한 루프 범위를 설정함
  2. 인접한 데이터 값을 비교함
  3. swap 조건에 부합하면 swap 연산을 수행함
  4. 루프 범위가 끝날 때까지 2~3을 반복함
  5. 정렬 영역을 설정함
  6. 비교 대상이 없을 때까지 1~5를 반복함

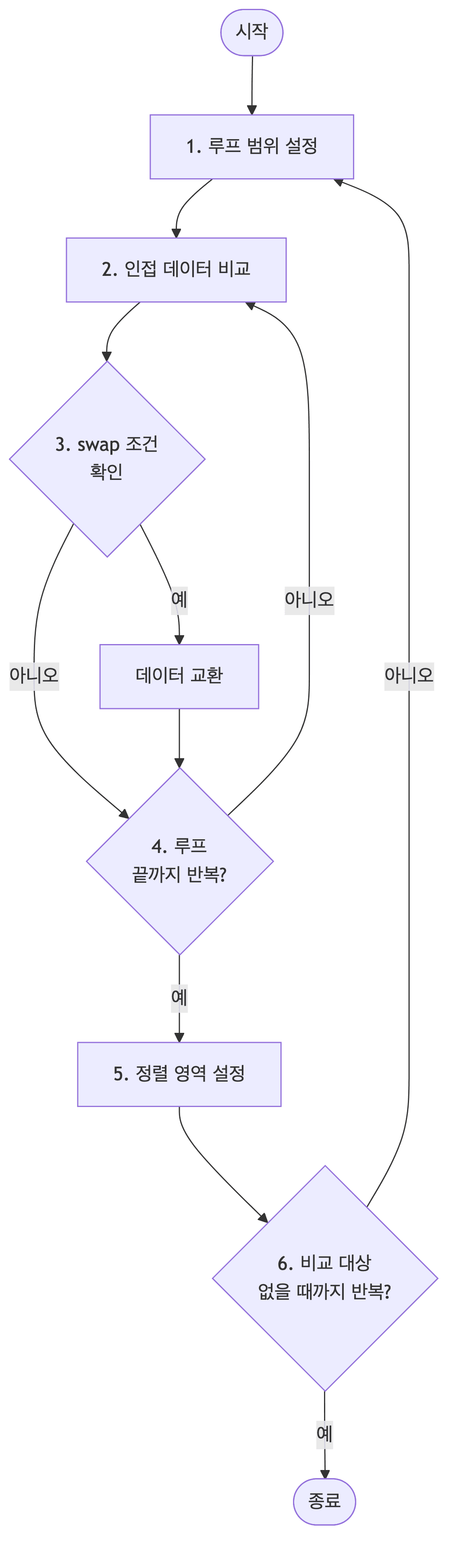
• 만약 특정한 루프의 전체 영역에서 swap이 한 번도 발생하지 않았다면 그 영역 뒤에 있는 데이터가 모두 정렬됐다는 뜻이므로 프로세스를 종료해도 됨

void bubbleSort(int[] array) {
    int n = array.length;
    for (int i = 0; i < n - 1; i++) {
        boolean swapped = false;
        for (int j = 0; j < n - 1 - i; j++) {
            if (array[j] > array[j + 1]) {
                int temp = array[j];
                array[j] = array[j + 1];
                array[j + 1] = temp;
                swapped = true;
            }
        }
        if (!swapped) break;
    }
}

선택 정렬

• 현재 위치부터 끝까지 배열을 탐색하여 최솟값을 찾은 후, 현재 위치의 값과 교환함
• 가장 작은 요소부터 차례로 앞으로 이동함

• 버블 정렬보다 교환 횟수가 적어 조금 더 빠름

• 시간 복잡도
  • 모든 경우
    • $O(n^2)$
• 공간 복잡도
  • $O(1)$

• 안정성

  • 불안정적임

• 원리

  • 대상 데이터에서 최대나 최소 데이터를 데이터가 나열된 순으로 찾아가며 선택하는 방법임
  • 구현 방법이 복잡하고, 시간 복잡도도 $O(n^2)$으로 효율적이지 않음

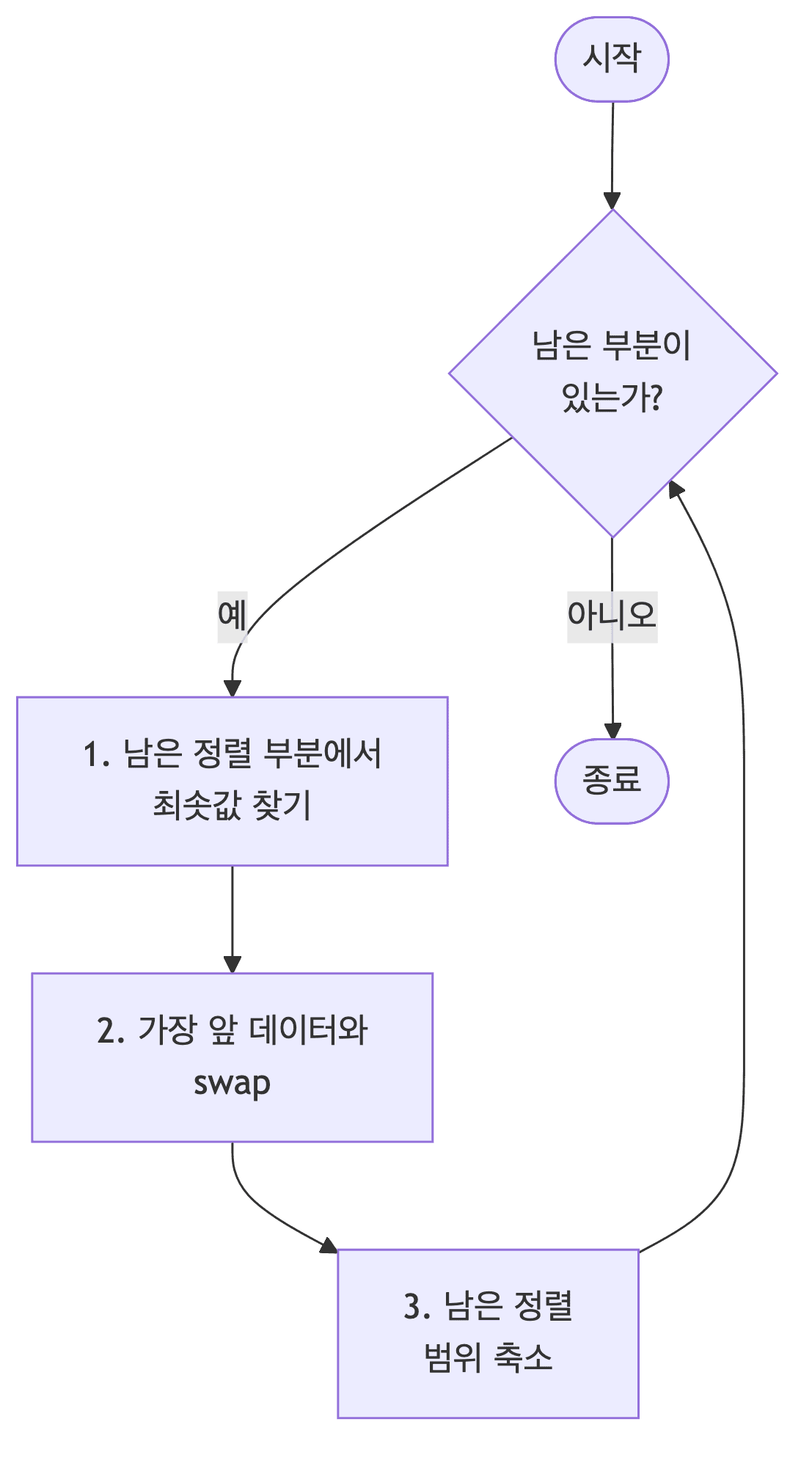
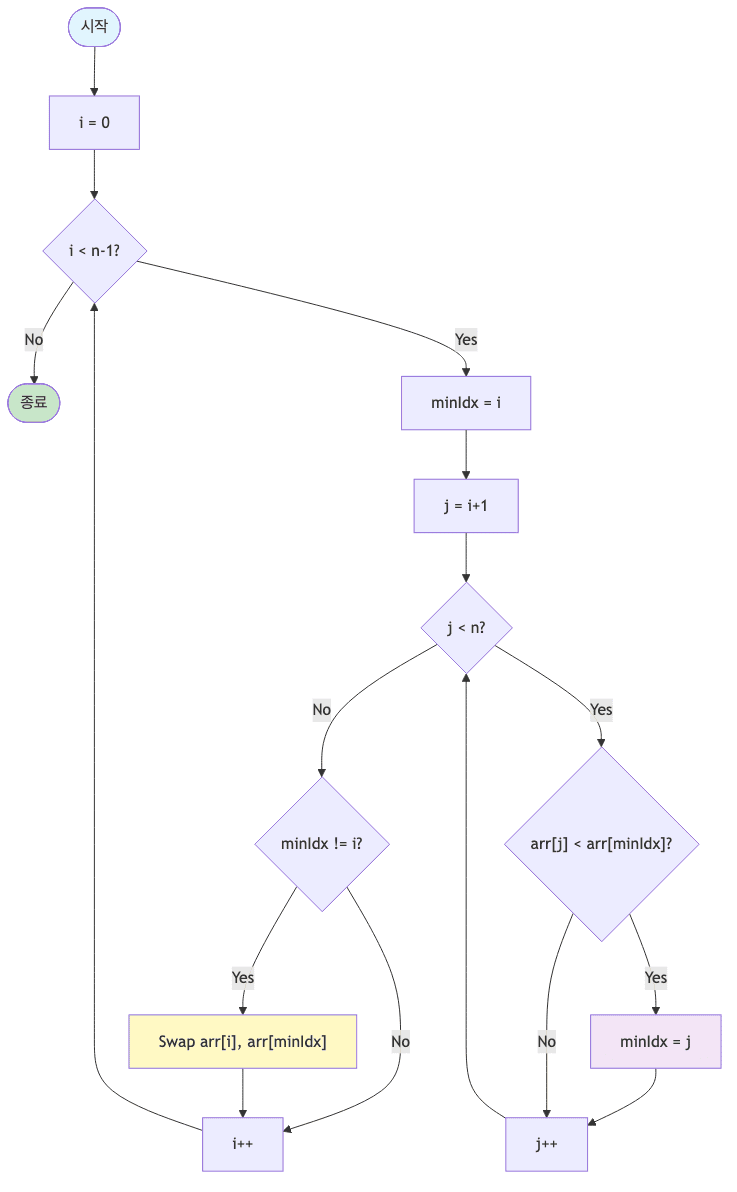
• 과정

  1. 남은 정렬 부분에서 최솟값 또는 최댓값을 찾음
  2. 남은 정렬 부분에서 가장 앞에 있는 데이터와 선택된 데이터를 swap함
  3. 가장 앞에 있는 데이터의 위치를 변경해 남은 정렬 부분의 범위를 축소함
  4. 전체 데이터 크기만큼 남은 정렬 부분이 없을 때까지 반복함

void selectionSort(int[] array) {
    int n = array.length;
    for (int i = 0; i < n - 1; i++) {
        int minIdx = i;
        for (int j = i + 1; j < n; j++) {
            if (array[j] < array[minIdx]) {
                minIdx = j;
            }
        }
        int temp = array[i];
        array[i] = array[minIdx];
        array[minIdx] = temp;
    }
}

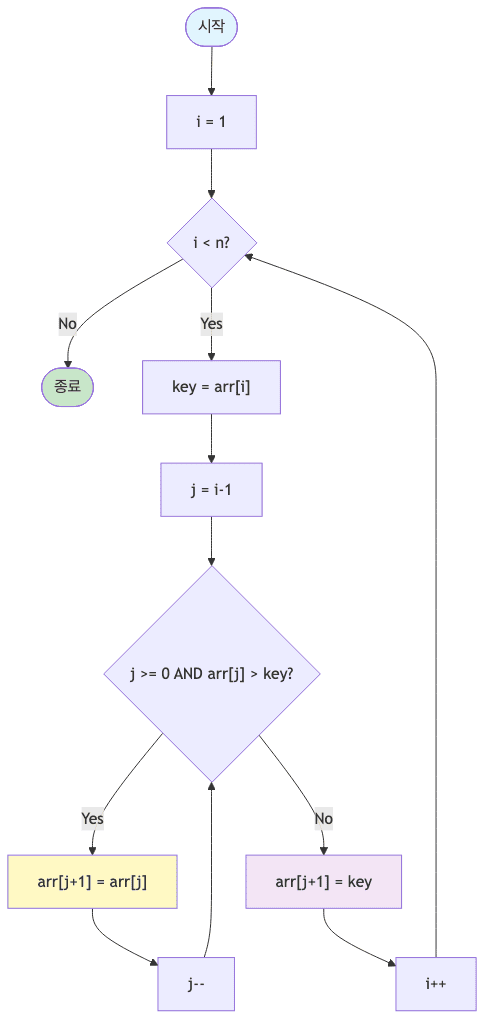
삽입 정렬

• 배열의 두 번째 요소부터 시작하여, 각 요소를 이미 정렬된 부분 배열의 올바른 위치에 삽입함
• 카드 게임에서 카드를 정렬하는 방식과 유사함

• 작은 데이터셋에 효율적이며, 거의 정렬된 상태의 데이터에서 매우 빠름

• 시간 복잡도
  • 평균
    • $O(n^2)$
  • 최악
    • $O(n^2)$
  • 최선
    • $O(n)$
• 공간 복잡도
  • $O(1)$

• 안정성

  • 안정적임

• 원리

  • 이미 정렬된 데이터 범위에 정렬되지 않은 데이터를 적절한 위치에 삽입시켜 정렬하는 방식임
  • 선택 데이터를 현재 정렬된 데이터 범위 내에서 적절한 위치에 삽입함

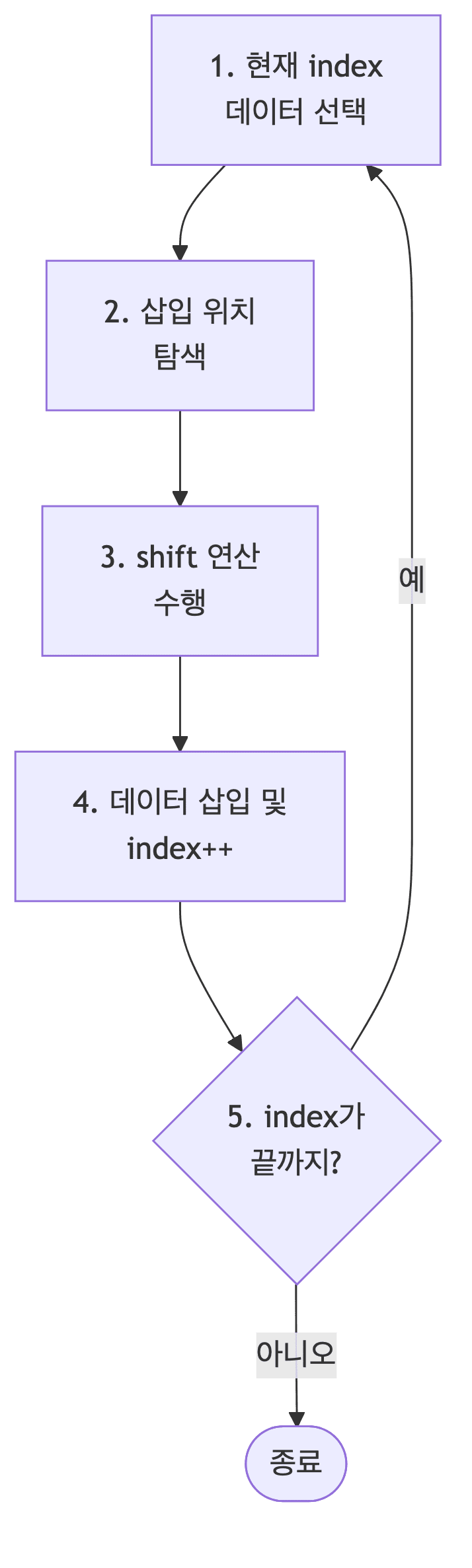
• 과정

  1. 현재 index에 있는 데이터 값을 선택함
  2. 현재 선택한 데이터가 정렬될 데이터 범위에 삽입될 위치를 탐색함
  3. 삽입 위치부터 index에 있는 위치까지 shift 연산을 수행함
  4. 삽입 위치에 현재 선택한 데이터를 삽입하고 index++ 연산을 수행함
  5. 전체 데이터의 크기만큼 index가 커질 때까지 반복함

void insertionSort(int[] array) {
    for (int i = 1; i < array.length; i++) {
        int key = array[i];
        int j = i - 1;
        while (j >= 0 && array[j] > key) {
            array[j + 1] = array[j];
            j--;
        }
        array[j + 1] = key;
    }
}

병합 정렬

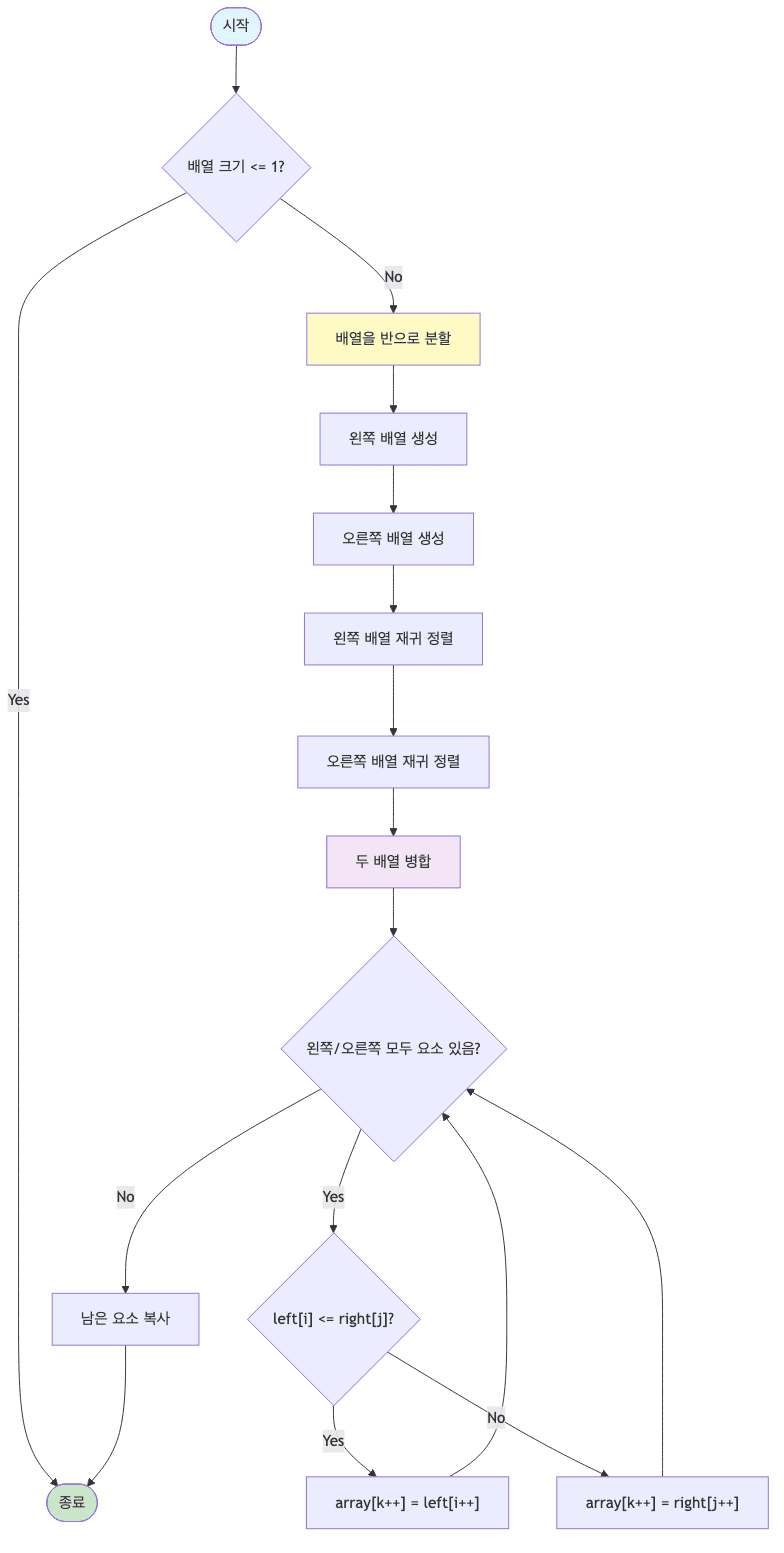
• 분할 정복 기법을 사용함
• 배열을 반으로 나누어 각각 정렬한 후, 정렬된 두 배열을 병합함

• 항상 일정한 성능을 보장함

• 시간 복잡도
  • 모든 경우
    • $O(n \log n)$
• 공간 복잡도
  • $O(n)$

• 안정성

  • 안정적임

• 원리

  • 분할 정복을 분할하고 분할한 집합을 정렬하며 합치는 알고리즘임
  • 최초에는 8개의 그룹으로 나뉨
  • 2개씩 그룹을 합치며 오름차순 정렬함
  • 이런 방식으로 병합 정렬 과정을 거치면 전체를 오름차순으로 정렬할 수 있음

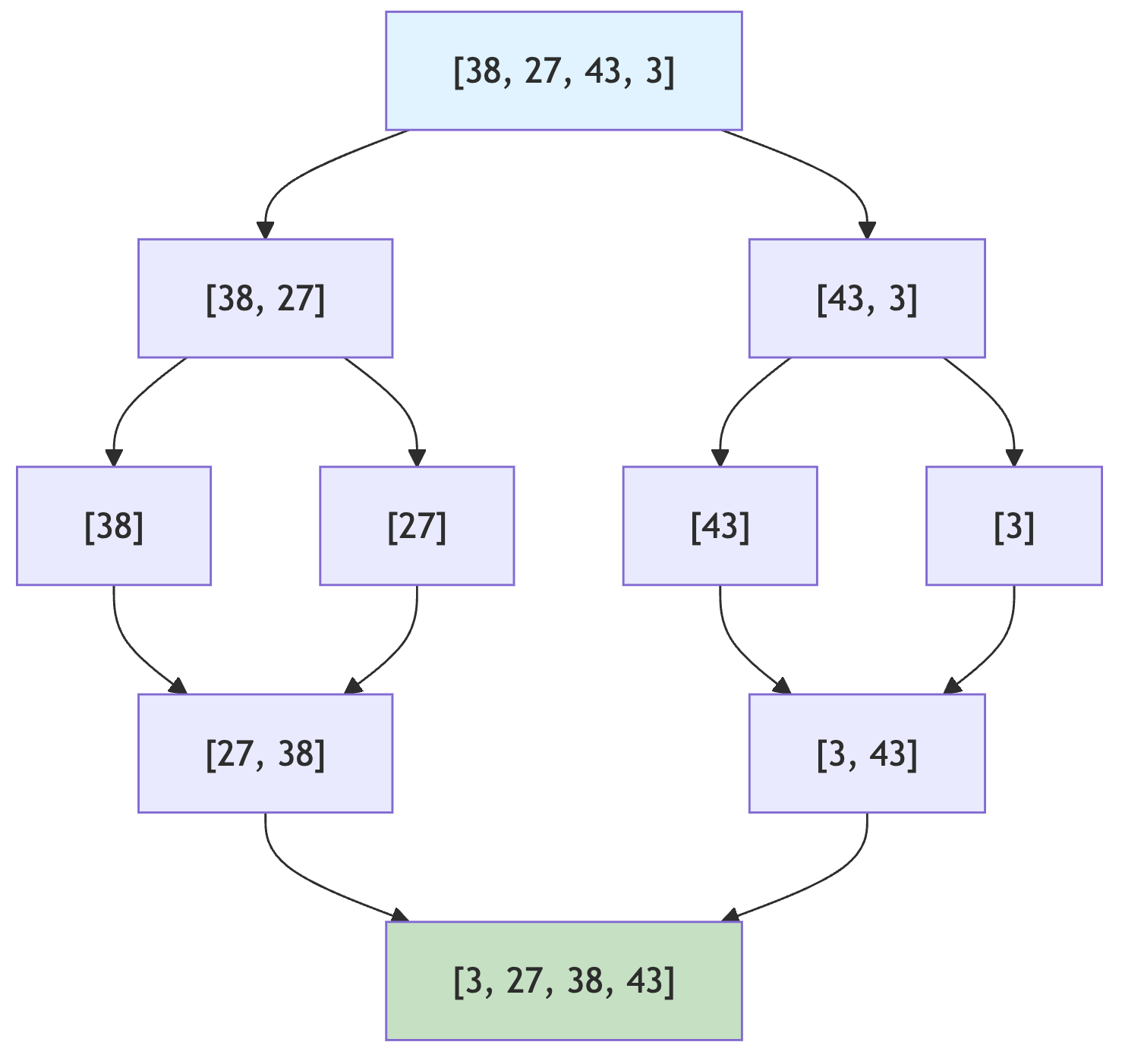
• 두 포인터 개념을 사용하여 왼쪽, 오른쪽 그룹을 병합함
• 왼쪽 포인터와 오른쪽 포인터의 값을 비교하여 작은 값을 결과 배열에 추가하고 포인터를 오른쪽으로 1칸 이동시킴

void mergeSort(int[] array) {
    if (array.length <= 1) return;

    int mid = array.length / 2;
    int[] left = new int[mid];
    int[] right = new int[array.length - mid];

    System.arraycopy(array, 0, left, 0, mid);
    System.arraycopy(array, mid, right, 0, array.length - mid);

    mergeSort(left);
    mergeSort(right);
    merge(array, left, right);
}

void merge(int[] array, int[] left, int[] right) {
    int i = 0, j = 0, k = 0;
    while (i < left.length && j < right.length) {
        array[k++] = left[i] <= right[j] ? left[i++] : right[j++];
    }
    while (i < left.length) array[k++] = left[i++];
    while (j < right.length) array[k++] = right[j++];
}

퀵 정렬

• 분할 정복 기법을 사용함
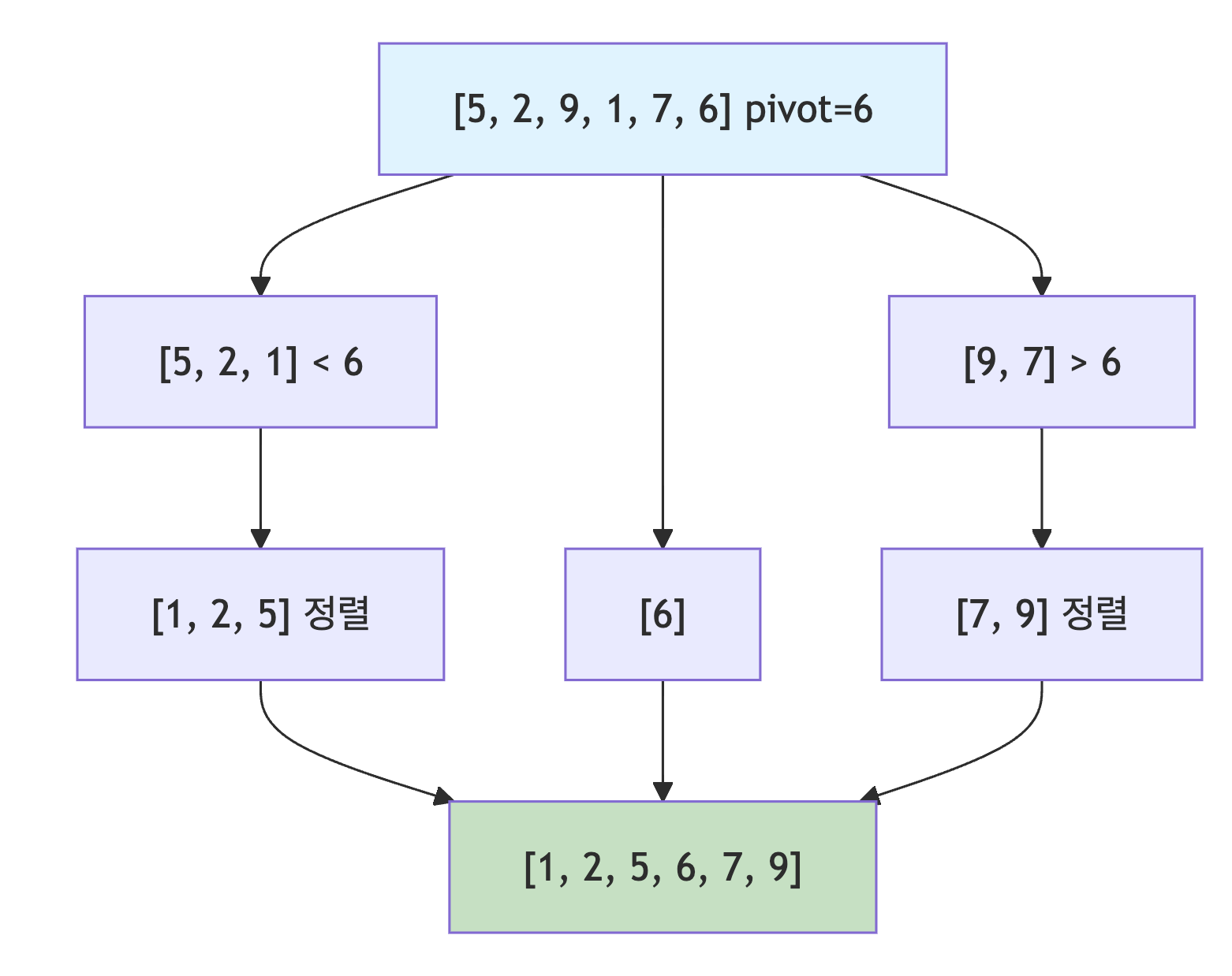
• 피벗이라는 기준값을 선택하여 배열을 분할한 후, 각 부분을 재귀적으로 정렬함
• 평균적으로 가장 많이 사용되는 정렬임

• 시간 복잡도
  • 평균
    • $O(n \log n)$
  • 최악
    • $O(n^2)$
• 공간 복잡도
  • $O(\log n)$

• 안정성

  • 불안정적임

• 원리

  • 기준값을 선정해 해당 값보다 작은 데이터와 큰 데이터로 분류하는 것을 반복해 정렬하는 알고리즘임
  • 기준값은 pivot이라고 함
  • pivot을 중심으로 계속 데이터를 2개의 집합으로 나누면서 정렬하는 것이 중요함

• 과정

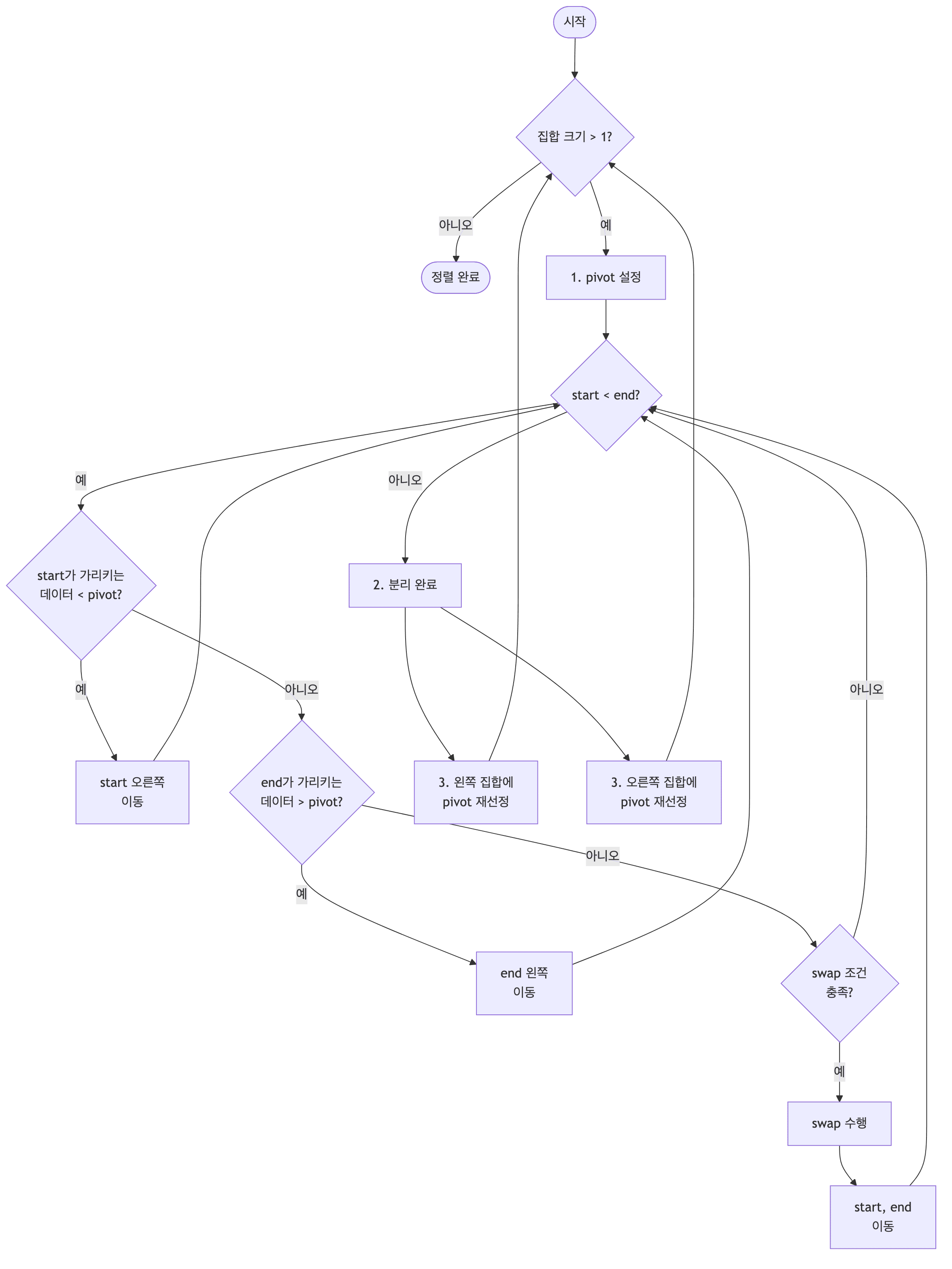
  1. 데이터를 분할하는 pivot을 설정함
  2. pivot을 기준으로 다음 과정을 거쳐 데이터를 2개의 집합으로 분리함
  • start가 가리키는 데이터가 pivot보다 작으면 start를 오른쪽으로 1칸 이동함
  • end가 가리키는 데이터가 pivot보다 크면 end를 왼쪽으로 1칸 이동함
  • start가 가리키는 데이터가 pivot보다 크고, end가 가리키는 데이터가 pivot보다 작으면 swap하고 start는 오른쪽, end는 왼쪽으로 1칸씩 이동함
  • start와 end가 만날 때까지 반복함
  • start와 end가 만나면 만난 지점의 데이터와 pivot을 비교하여 적절한 위치에 pivot을 삽입함
  1. 분리 집합에서 각각 다시 pivot을 선정함
  2. 분리 집합이 1개 이하가 될 때까지 과정 1~3을 반복함

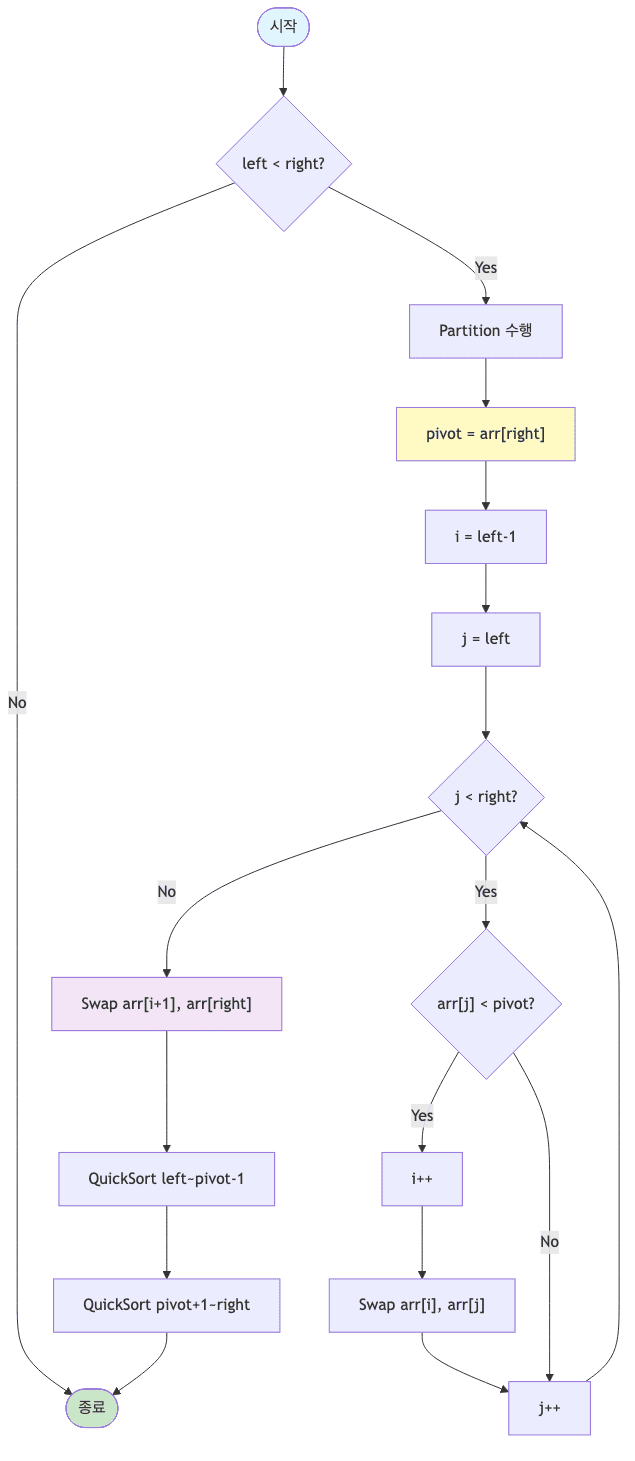
void quickSort(int[] array, int left, int right) {
    if (left < right) {
        int pivot = partition(array, left, right);
        quickSort(array, left, pivot - 1);
        quickSort(array, pivot + 1, right);
    }
}

int partition(int[] array, int left, int right) {
    int pivot = array[right];
    int i = left - 1;

    for (int j = left; j < right; j++) {
        if (array[j] < pivot) {
            i++;
            int temp = array[i];
            array[i] = array[j];
            array[j] = temp;
        }
    }

    int temp = array[i + 1];
    array[i + 1] = array[right];
    array[right] = temp;

    return i + 1;
}

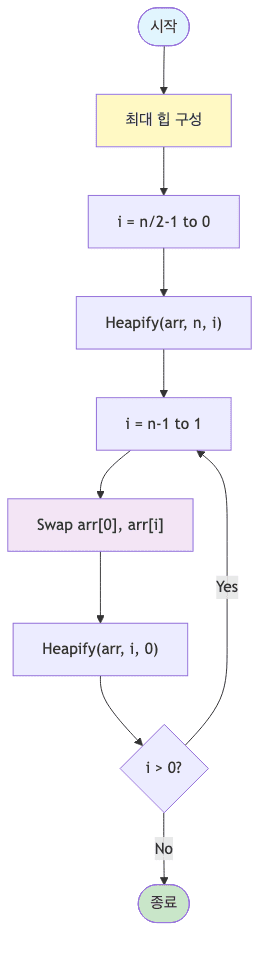
힙 정렬

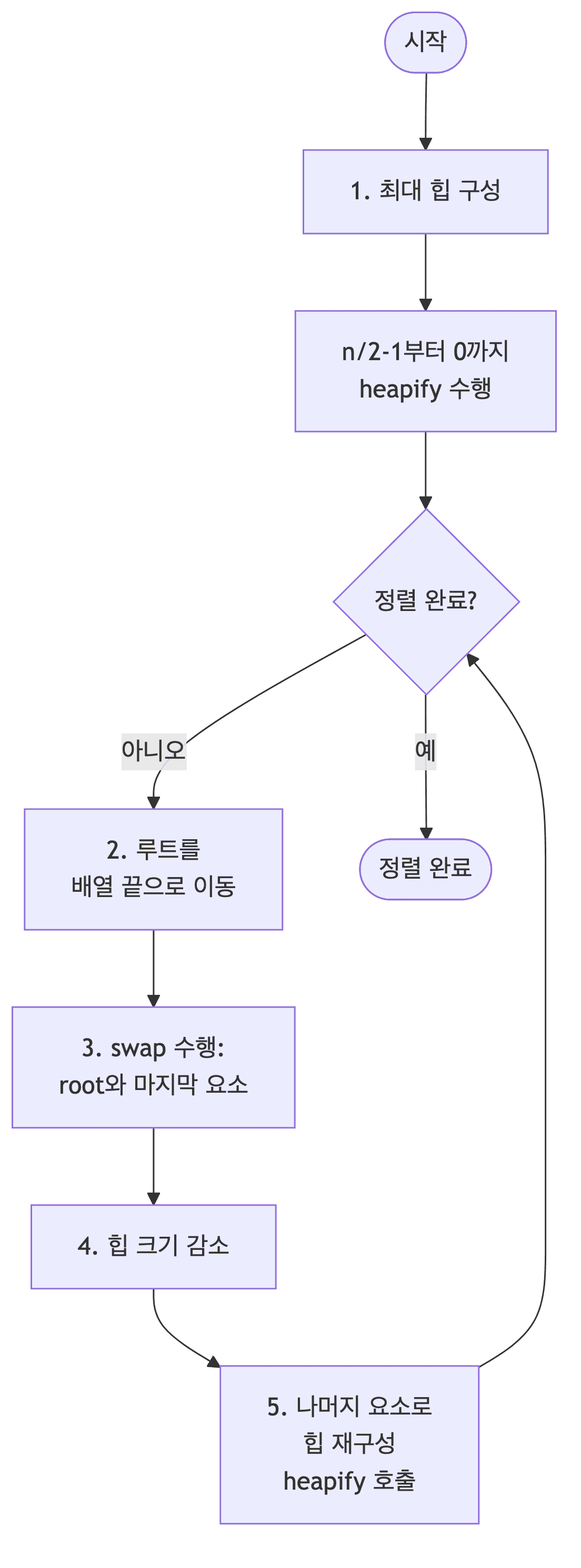
• 최대 힙을 구성한 후, 힙의 루트를 배열의 끝으로 이동함
• 나머지 요소들로 다시 힙을 구성하는 과정을 반복함

• 추가 메모리 없이 항상 $O(n \log n)$을 보장함

• 시간 복잡도
  • 모든 경우
    • $O(n \log n)$
• 공간 복잡도
  • $O(1)$
• 안정성
  • 불안정적임

void heapSort(int[] array) {
    int n = array.length;

    for (int i = n / 2 - 1; i >= 0; i--) {
        heapify(array, n, i);
    }

    for (int i = n - 1; i > 0; i--) {
        int temp = array[0];
        array[0] = array[i];
        array[i] = temp;

        heapify(array, i, 0);
    }
}

void heapify(int[] array, int n, int i) {
    int largest = i;
    int left = 2 * i + 1;
    int right = 2 * i + 2;

    if (left < n && array[left] > array[largest]) {
        largest = left;
    }

    if (right < n && array[right] > array[largest]) {
        largest = right;
    }

    if (largest != i) {
        int temp = array[i];
        array[i] = array[largest];
        array[largest] = temp;

        heapify(array, n, largest);
    }
}

정리

• 비교 정렬은 데이터 간의 비교 연산을 통해 정렬하는 알고리즘임
• 기초 정렬은 구현이 단순하지만 $O(n^2)$의 시간 복잡도를 가짐
• 고급 정렬은 분할 정복을 활용하여 $O(n \log n)$의 성능을 제공함
• 버블, 선택 정렬은 교육용으로 유용하지만 실전에서는 거의 사용하지 않음
• 삽입 정렬은 작은 데이터나 거의 정렬된 데이터에 효율적임
• 병합 정렬은 안정적이고 일정한 성능을 보장하지만 추가 메모리가 필요함
• 퀵 정렬은 평균적으로 가장 빠르지만 최악의 경우 $O(n^2)$가 될 수 있음
• 힙 정렬은 추가 메모리 없이 $O(n \log n)$을 보장함

Reference

• Do it! 알고리즘 코딩 테스트 - 자바 편