데이터베이스 인덱스

개요

데이터베이스 인덱스는 테이블의 데이터 검색 속도를 향상시키기 위한 자료 구조임
책의 색인과 유사하게 특정 데이터를 빠르게 찾을 수 있도록 정렬된 구조를 제공함
인덱스는 읽기 성능을 향상시키지만 쓰기 성능에는 오버헤드를 발생시킴

인덱스의 기본 원리

인덱스가 필요한 이유

테이블 전체 스캔은 데이터가 많아질수록 비효율적임
인덱스를 사용하면 특정 데이터를 빠르게 찾을 수 있음
정렬된 구조를 통해 범위 검색도 효율적으로 처리 가능

인덱스의 트레이드오프

읽기 성능 향상
- O(n) → O(log n)
쓰기 성능 저하
- INSERT, UPDATE, DELETE 시 인덱스 유지 비용 발생
- INSERT
  - 테이블에 데이터를 삽입할 때 인덱스에도 해당 키 값을 정렬된 위치에 삽입해야 함
- UPDATE
  - 인덱스 컬럼 값이 변경되면 기존 키를 삭제하고 새로운 키를 삽입해야 함
- DELETE
  - 테이블에서 데이터를 삭제할 때 인덱스에서도 해당 키를 찾아 삭제해야 함
- B+Tree 구조 유지
  - 삽입/삭제 시 트리 균형을 유지하기 위한 노드 분할/병합 작업 필요
- 여러 인덱스
  - 테이블에 인덱스가 여러 개 있으면 각 인덱스마다 작업이 반복됨
저장 공간 증가
- 인덱스 자체가 추가 저장 공간 필요

인덱스 사용 시점

WHERE 절에서 자주 사용되는 컬럼
JOIN 조건으로 사용되는 컬럼
ORDER BY, GROUP BY에 사용되는 컬럼
UNIQUE 제약이 필요한 컬럼

주요 인덱스 타입

B-Tree 계열 인덱스 (B+Tree)

현대 RDBMS(MySQL InnoDB, Oracle, PostgreSQL 등)에서 기본 인덱스 타입으로 사용되는 구조임
엄밀히 말하면 B-Tree의 변형인 B+Tree를 사용하며 B-Tree와의 주요 차이점은 다음과 같음
- 브랜치 노드에는 키 값만 저장되고 실제 데이터는 저장되지 않음
- 리프 노드에만 데이터 포인터(ROWID)가 저장됨
- 리프 노드들이 Linked List로 연결되어 순차 검색(Range Scan)이 효율적임
균형 잡힌 트리 구조를 통해 로그 시간 복잡도(O(log n))를 보장하며 모든 리프 노드가 동일한 레벨에 위치하여 균일한 접근 시간을 유지함
범위 쿼리와 정확한 매칭 모두에 효율적임

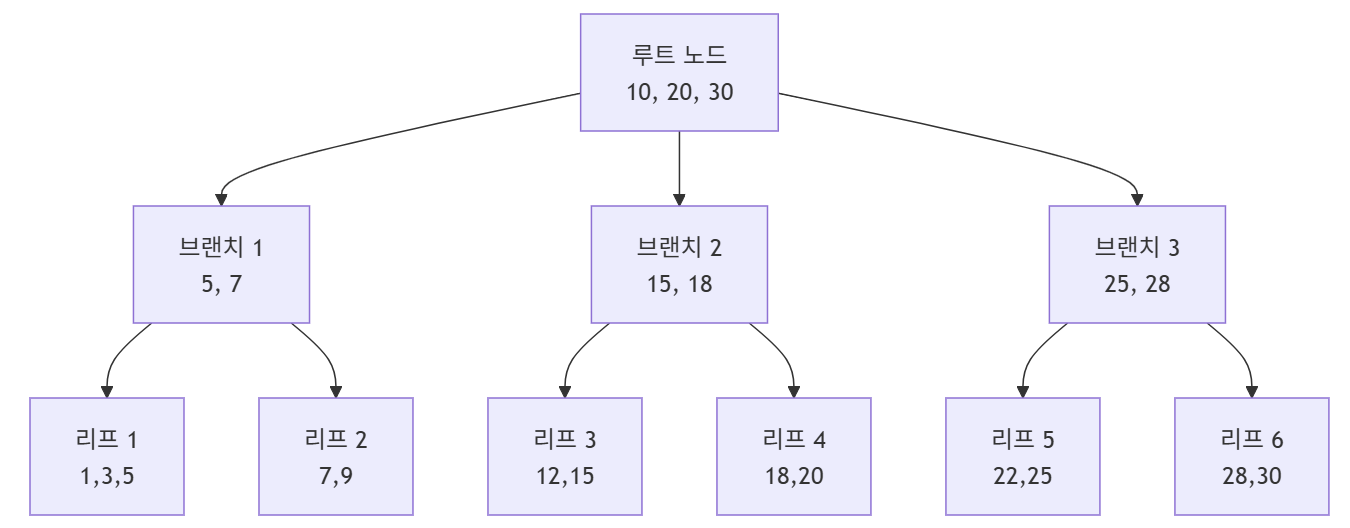
B+Tree 구조

루트 노드
- 트리의 최상위 노드, 키 값만 포함
브랜치 노드
- 중간 레벨의 노드들, 키 값과 자식 노드 포인터만 포함
리프 노드
- 최하위 레벨의 노드들, 키 값과 실제 데이터 포인터(ROWID)를 포함하며 Linked List로 연결됨
각 노드는 여러 키와 자식 노드 포인터를 포함함

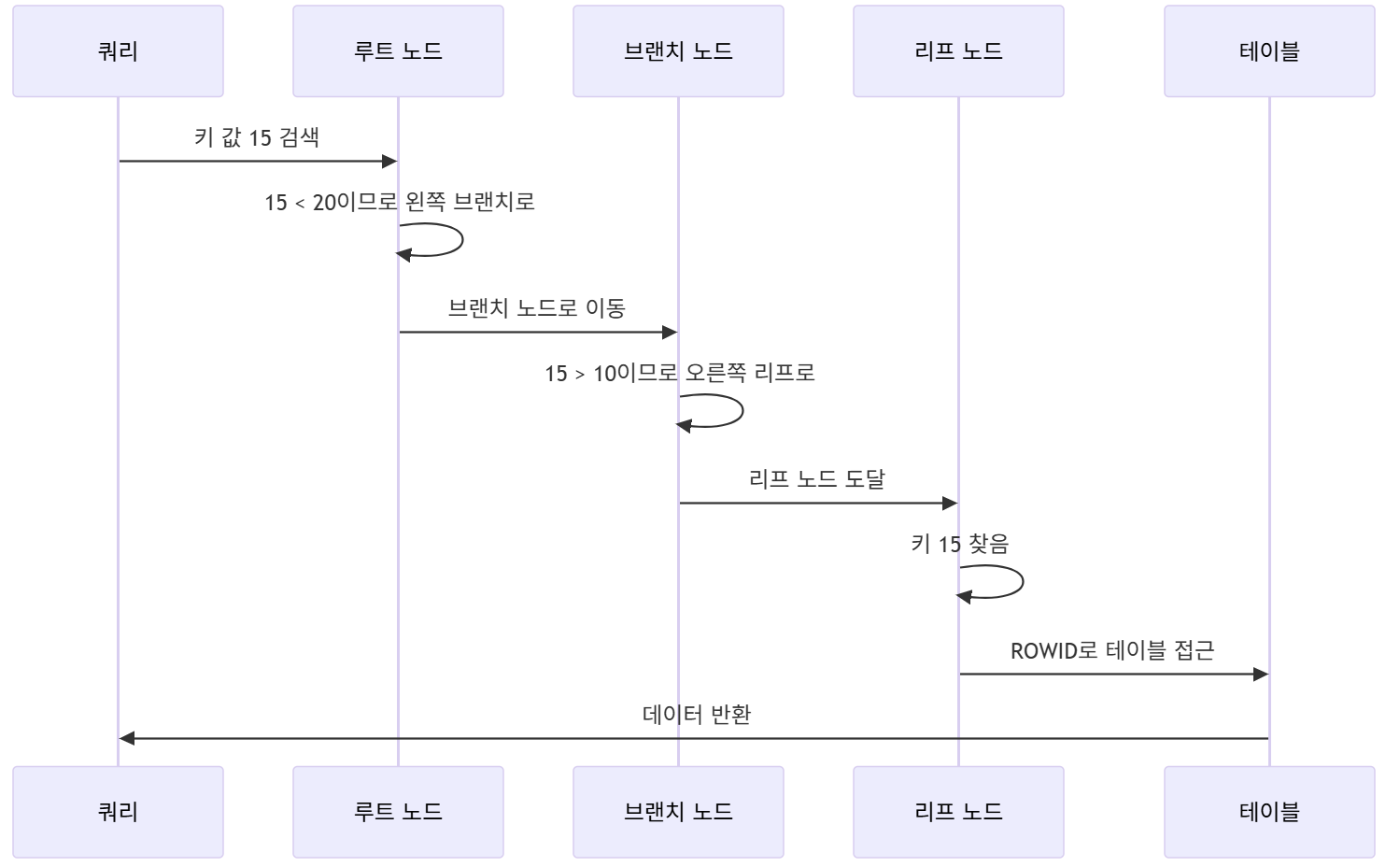
B+Tree 검색 과정

루트 노드에서 시작하여 키 값을 비교
적절한 브랜치 노드로 이동 (브랜치 노드에는 키만 있으므로 빠른 탐색 가능)
리프 노드에 도달할 때까지 반복
리프 노드에서 키를 찾고 데이터 포인터(ROWID)를 통해 실제 데이터 접근
범위 검색 시 리프 노드의 Linked List를 따라 순차 스캔 가능

B+Tree 특징

균형 트리 구조로 일관된 검색 성능 제공
범위 쿼리와 정확한 매칭 모두 지원
정렬된 데이터 구조로 ORDER BY 최적화 가능
리프 노드들이 Linked List로 연결되어 있어 범위 스캔에 매우 효율적 (B+Tree의 핵심 특징)
브랜치 노드에 데이터가 없어 더 많은 키를 저장할 수 있어 트리 높이가 낮아짐

Hash 인덱스

해시 함수를 사용하여 키를 인덱스 위치에 매핑함
정확한 매칭 쿼리에서 매우 빠른 성능을 제공하지만 범위 쿼리에는 적합하지 않음
충돌 해결 기법을 통해 동일한 해시 값을 가진 경우를 처리함
특징
- O(1) 평균 검색 시간 제공
- 등호 연산(=)에 최적화
- 범위 쿼리, 정렬 작업에는 비효율적
사용 사례
- 메모리 기반 테이블(MySQL MEMORY 엔진)
- 정확한 키 조회가 주된 작업인 경우

Bitmap 인덱스

낮은 카디널리티(distinct value가 적은) 컬럼에 효과적임
각 distinct 값에 대해 비트맵을 생성하며 AND, OR, XOR 같은 비트 연산을 통해 빠른 쿼리 성능을 제공함
성별, 상태 코드 같은 컬럼에 적합함
특징
- 낮은 카디널리티 컬럼에 최적화
- 비트 연산을 통한 빠른 집합 연산
- 저장 공간 효율적(낮은 카디널리티일 때)
사용 사례
- 성별, 결혼 여부, 상태 코드 등
- 데이터 웨어하우스(DW) 환경
- 복합 조건 쿼리가 빈번한 경우
주의 사항
- MySQL이나 PostgreSQL 같은 범용 웹 RDBMS의 기본 스토리지 엔진에서는 비트맵 인덱스를 지원하지 않음
- 주로 Oracle, Enterprise급 DB, 또는 특정 분석용 엔진에서 지원됨
- 데이터 웨어하우스나 엔터프라이즈 DB 환경에서 주로 사용됨

클러스터드 vs 논클러스터드 인덱스

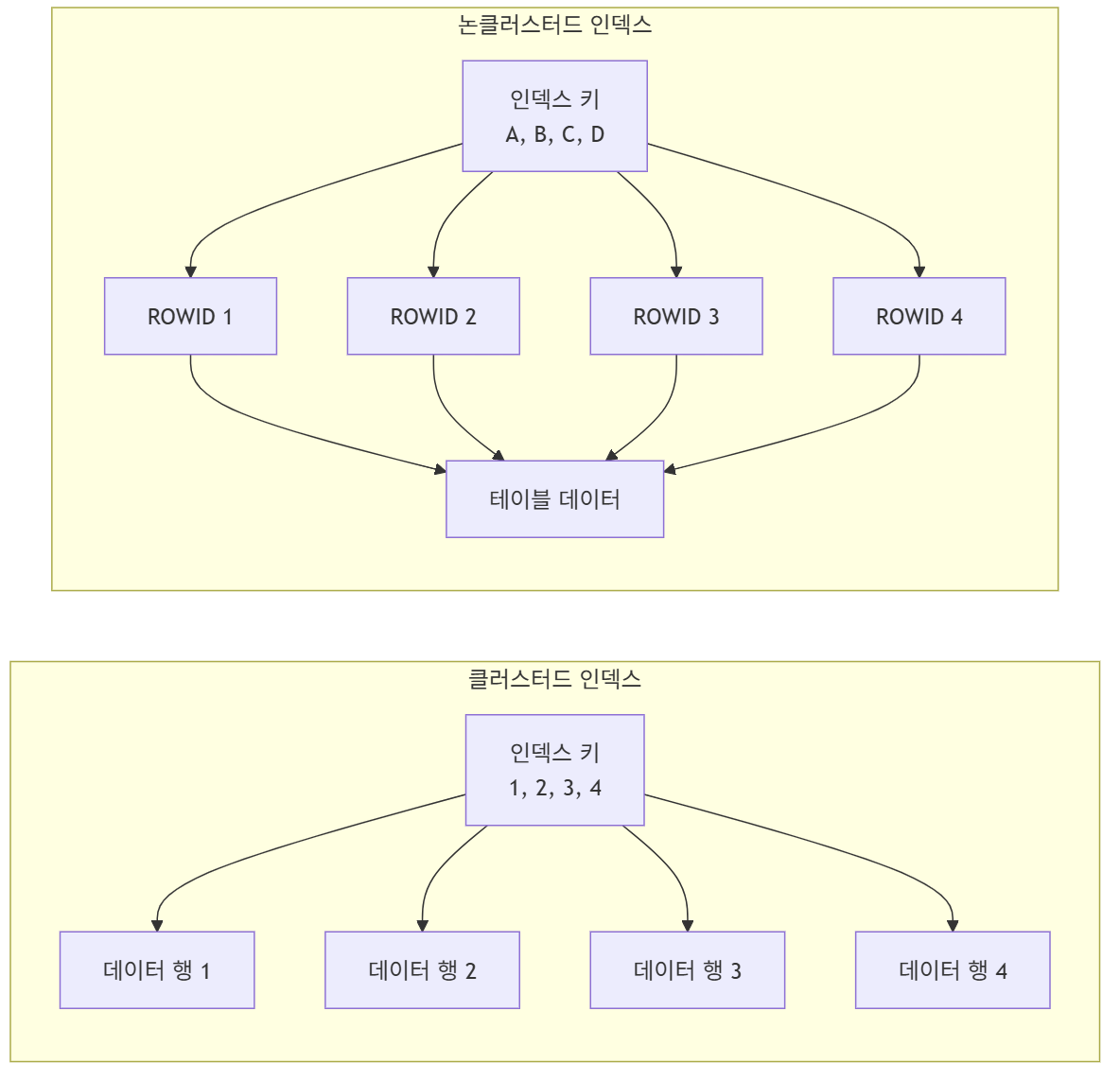
MySQL InnoDB의 경우, 논클러스터드 인덱스는 ROWID 대신 기본 키(PK) 값을 저장하며 PK로 클러스터드 인덱스를 다시 검색하는 Double Lookup이 발생함

클러스터드 인덱스

테이블 데이터의 물리적 순서를 결정함
테이블당 하나만 존재할 수 있으며 인덱스 자체가 데이터를 포함하므로 추가 저장 공간이 필요하지 않음
범위 쿼리와 정렬 작업에 매우 빠름
DBMS별 동작 차이
- MySQL InnoDB
  - Primary Key가 클러스터드 인덱스로 강제됨 (PK가 없으면 숨겨진 클러스터드 인덱스 생성)
- PostgreSQL
  - 기본적으로 Heap 테이블 구조를 사용하며 Primary Key는 논클러스터드 인덱스와 유사하게 동작함
  - 물리적 정렬을 원하면 CLUSTER 명령어를 사용해야 하며 이마저도 자동으로 유지되지 않음
- SQL Server
  - 클러스터드 인덱스를 명시적으로 지정 가능
특징
- 테이블당 하나만 존재 가능
- 물리적 데이터 순서 결정
- 추가 저장 공간 불필요
- 범위 쿼리에 최적화
장점
- 범위 스캔 시 연속된 데이터 블록 읽기로 I/O 효율적
- 정렬 작업이 불필요한 경우가 많음
- 인덱스와 데이터가 함께 저장되어 조회 성능 우수
단점
- 삽입/수정 시 데이터 재정렬 필요로 성능 저하 가능
- 테이블당 하나만 생성 가능

논클러스터드 인덱스

데이터와 별도로 저장되는 구조로 인덱스 컬럼과 실제 데이터 행을 찾을 수 있는 값을 포함함
테이블당 여러 개 생성 가능하며 추가 저장 공간이 필요함
특정 컬럼 검색에는 효율적이지만 실제 데이터를 가져오기 위해 추가 조회(lookup) 단계가 필요함
DBMS별 포인터 저장 방식의 차이
- PostgreSQL / Oracle
  - 실제 데이터의 물리적 주소인 ROWID(또는 TID)를 저장함
  - 인덱스에서 바로 데이터 위치를 찾아가므로 조회가 빠름
- MySQL InnoDB
  - 물리적 주소 대신 기본 키(PK) 값을 저장함
  - 인덱스에서 PK를 찾은 후, 다시 클러스터드 인덱스(PK 인덱스)를 검색해서 데이터를 가져옴 (Double Lookup 발생)
  - 데이터 이동(Page Split 등) 시 세컨더리 인덱스를 갱신할 필요가 없어 쓰기 성능에 이점이 있음
특징
- 테이블당 여러 개 생성 가능
- 별도 저장 공간 필요
- 인덱스 키와 데이터 포인터 저장 (DBMS별로 ROWID 또는 PK 값)
- 추가 조회 단계 필요
장점
- 여러 컬럼에 대해 인덱스 생성 가능
- 삽입/수정 시 데이터 재정렬 불필요
- 유연한 인덱스 설계 가능
단점
- 데이터 접근 시 추가 조회 단계 필요 (MySQL InnoDB는 Double Lookup)
- 추가 저장 공간 필요
- 클러스터드 인덱스보다 범위 쿼리 성능 낮음

복합 인덱스

여러 컬럼에 대해 생성되는 인덱스로 MySQL에서는 최대 16개 컬럼까지 지정 가능함
컬럼 순서가 매우 중요하며 leftmost prefix 원칙을 따름

Leftmost Prefix 원칙

인덱스가 (A, B, C) 순서로 생성된 경우

(A), (A, B), (A, B, C) 조건을 사용하는 쿼리에서 인덱스 활용 가능
(B), (C), (B, C) 조건만으로는 인덱스 사용 불가

  
-- 인덱스 - last_name, first_name, age

-- 인덱스 사용 가능
SELECT * FROM users WHERE last_name = 'Kim';
SELECT * FROM users WHERE last_name = 'Kim' AND first_name = 'John';
SELECT * FROM users WHERE last_name = 'Kim' AND first_name = 'John' AND age = 30;

-- 인덱스 사용 가능하지만 효율성 차이
SELECT * FROM users WHERE last_name = 'Kim' AND age = 30;
-- last_name으로 인덱스 스캔은 가능하지만 age 조건은 인덱스 필터링 단계에서 처리됨
-- MySQL 8.0 이전 버전에서는 Index Skip Scan이 없어 first_name을 건너뛰지 못해 효율이 떨어질 수 있음

-- 인덱스 사용 불가
SELECT * FROM users WHERE first_name = 'John';
SELECT * FROM users WHERE age = 30;
SELECT * FROM users WHERE first_name = 'John' AND age = 30;

복합 인덱스 동작 원리

인덱스는 첫 번째 컬럼으로 정렬되고 같은 값 내에서 두 번째 컬럼으로 정렬됨
(A, B, C) 인덱스는 A → B → C 순서로 정렬됨
선행 컬럼이 없으면 정렬된 구조를 활용할 수 없음

설계 고려 사항

자주 함께 사용되는 컬럼 조합에 생성
카디널리티가 높은 컬럼을 앞에 배치
WHERE 절에서 자주 사용되는 컬럼 순서 고려
등호 조건이 있는 컬럼을 범위 조건보다 앞에 배치
ORDER BY 절의 컬럼 순서도 고려

카디널리티의 중요성

카디널리티
- 컬럼의 distinct 값의 개수
높은 카디널리티
- 거의 고유한 값
- ex) 이메일, 주민등록번호
낮은 카디널리티
- 적은 distinct 값
- ex) 성별, 상태 코드
인덱스 효과
- 높은 카디널리티 컬럼이 앞에 있을수록 효과적
이유
- 필터링 효과가 크기 때문

커버링 인덱스

쿼리에 필요한 모든 컬럼을 인덱스에 포함시켜 테이블 접근 없이 인덱스만으로 쿼리를 처리할 수 있게 하는 기법
Index-Only Scan을 가능하게 하여 디스크 I/O를 크게 줄이고 쿼리 성능을 향상시킴
특징
- 테이블 접근 없이 인덱스만으로 쿼리 처리
- 디스크 I/O 감소로 성능 향상
- 인덱스 크기 증가로 인한 트레이드오프 존재
장점
- 테이블 랜덤 액세스 제거로 성능 향상
- 특히 읽기 중심 워크로드에서 효과적
단점
- 인덱스 크기 증가
- 인덱스 유지 비용 증가

PostgreSQL의 INCLUDE 구문

PostgreSQL에서는 CREATE INDEX ... INCLUDE 구문을 통해 검색 키가 아닌 컬럼도 인덱스에 포함시킬 수 있음

  
-- 검색 키 - user_id
-- 포함 컬럼 - email, name
CREATE INDEX idx_user_covering ON users(user_id) INCLUDE (email, name);

-- 테이블 접근 없이 인덱스만으로 처리 가능
SELECT email, name FROM users WHERE user_id = 123;

커버링 인덱스 동작 비교

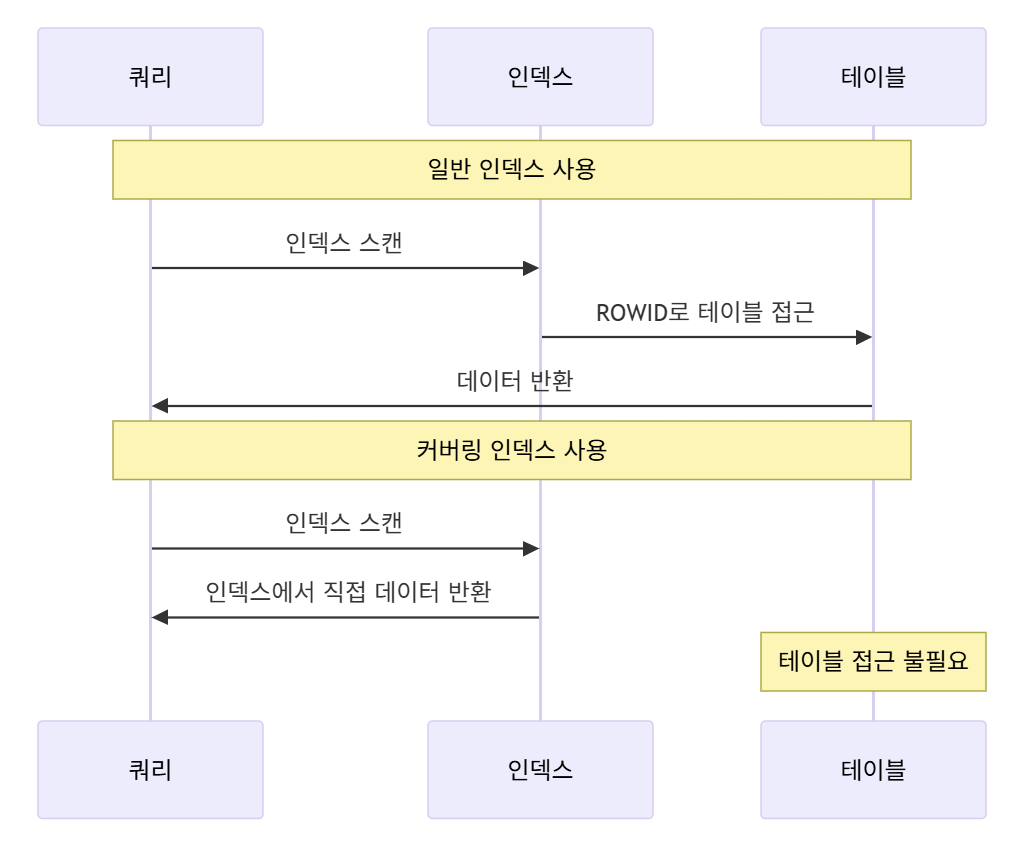
인덱스 선택도와 성능

선택도

선택도
- (조건을 만족하는 행 수) / (전체 행 수)
선택도가 낮을수록 인덱스가 효과적임
일반적으로 선택도가 5-10% 이하일 때 인덱스 사용이 유리함

인덱스 사용 여부 결정

옵티마이저가 통계 정보를 기반으로 비용 계산
인덱스 스캔 비용 vs 테이블 풀 스캔 비용 비교
선택도가 높으면 테이블 풀 스캔이 더 효율적일 수 있음

인덱스 통계 정보

카디널리티
- 각 인덱스 키의 distinct 값 개수
히스토그램
- 값 분포 정보
NULL 값 비율
통계 정보가 오래되면 옵티마이저가 잘못된 선택을 할 수 있음

인덱스 유지 비용

INSERT
- 새로운 키를 적절한 위치에 삽입
- B+Tree에서 삽입 위치 탐색
  - O(log n)
- 노드가 가득 차면 노드 분할(split) 발생
- 상위 노드까지 분할이 전파될 수 있음
UPDATE
- 키 값 변경 시 인덱스 재정렬 필요
- 기존 키 삭제
  - O(log n)
- 새로운 키 삽입
  - O(log n)
- 인덱스 컬럼이 변경되지 않아도 테이블 데이터 변경으로 인덱스 업데이트 필요할 수 있음
DELETE
- 인덱스에서 키 제거
- 삭제할 키 탐색
  - O(log n)
- 키 삭제 후 노드가 비면 병합(merge) 작업 발생
인덱스가 많을수록 쓰기 성능 저하
- 테이블에 인덱스가 5개면 INSERT 시 5번의 인덱스 삽입 작업 필요
- 각 인덱스마다 독립적인 B+Tree 구조 유지 작업 수행

인덱스 삽입 과정

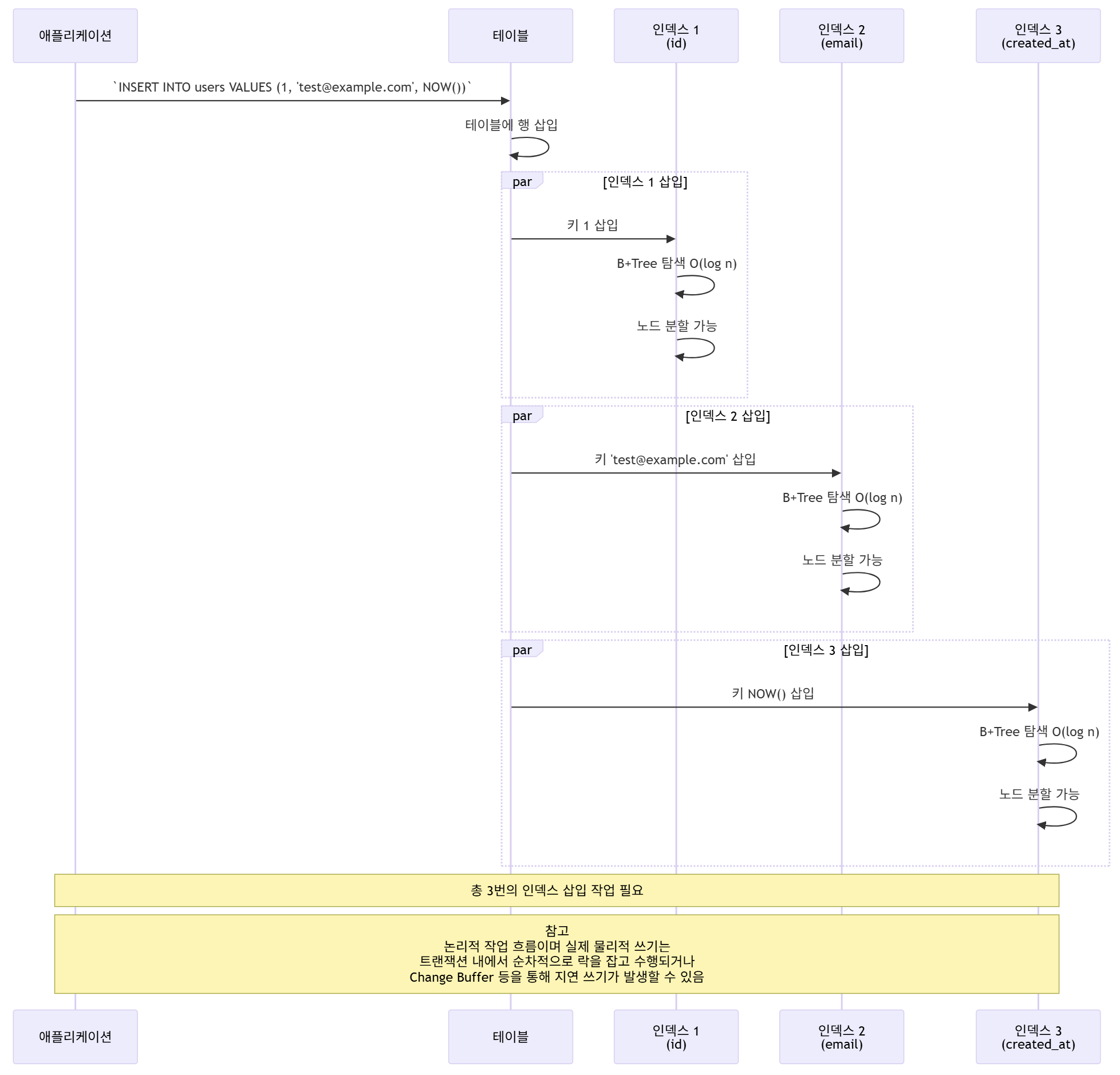
인덱스 설계 가이드

인덱스 생성 전략

쿼리 패턴 분석
- 자주 실행되는 쿼리 파악
WHERE 절 컬럼 우선 순위 결정
카디널리티 분석
인덱스 개수 제한
- 테이블당 5-10개 권장

인덱스 모니터링

사용되지 않는 인덱스 제거
중복 인덱스 확인
인덱스 조각화 모니터링
통계 정보 갱신 주기 설정

인덱스 최적화

인덱스 재구성
- 조각화 제거
통계 정보 갱신
- ANALYZE 명령 실행
인덱스 병합
- 여러 인덱스를 하나로 통합 고려
파티션 된 테이블의 경우 파티션별 인덱스 고려

주의 사항

와일드카드 패턴
- LIKE 'value%'
  - 인덱스 사용 가능 (Leftmost Prefix 원칙 적용)
- LIKE '%value%'
  - 인덱스 사용 불가 (문자열 앞부분을 알 수 없어 풀 스캔 발생)
함수나 연산
- WHERE salary * 1.1 > 100 처럼 컬럼을 가공하면 인덱스 사용 불가
NULL 값
- DBMS에 따라 인덱스 포함 여부가 다르지만 일반적으로 인덱스 효율이 떨어짐
작은 테이블
- 인덱스 오버헤드가 더 클 수 있음

결론

인덱스는 쿼리 성능 향상의 핵심이지만 과도한 인덱스는 쓰기 성능 저하를 유발할 수 있음
인덱스 설계 시 쿼리 패턴과 데이터 특성을 종합적으로 고려해야 함

데이터베이스 인덱스

개요

인덱스의 기본 원리

인덱스가 필요한 이유

인덱스의 트레이드오프

인덱스 사용 시점

주요 인덱스 타입

B-Tree 계열 인덱스 (B+Tree)

B+Tree 구조

B+Tree 검색 과정

B+Tree 특징

Hash 인덱스

Bitmap 인덱스

클러스터드 vs 논클러스터드 인덱스

클러스터드 인덱스

논클러스터드 인덱스

복합 인덱스

Leftmost Prefix 원칙

복합 인덱스 동작 원리

설계 고려 사항

카디널리티의 중요성

커버링 인덱스

PostgreSQL의 INCLUDE 구문

커버링 인덱스 동작 비교

인덱스 선택도와 성능

선택도

인덱스 사용 여부 결정

인덱스 통계 정보

인덱스 유지 비용

인덱스 삽입 과정

인덱스 설계 가이드

인덱스 생성 전략

인덱스 모니터링

인덱스 최적화

주의 사항

결론

Further Reading

[데이터베이스 시스템] 7강 - SQL

[데이터베이스 시스템] 8강 - 정규화

[데이터베이스 시스템] 9강 - 저장 객체