분할 정복 알고리즘이란?

개요

• 분할 정복은 큰 문제를 작은 부분 문제로 나누어 각각을 해결한 후, 그 결과를 결합하여 원래 문제를 해결하는 알고리즘 설계 패러다임임
• 복잡한 문제를 관리 가능한 작은 부분으로 분해함으로써 해결 과정을 단순화함
• 재귀적 접근 방식을 활용하여 문제를 효율적으로 해결함

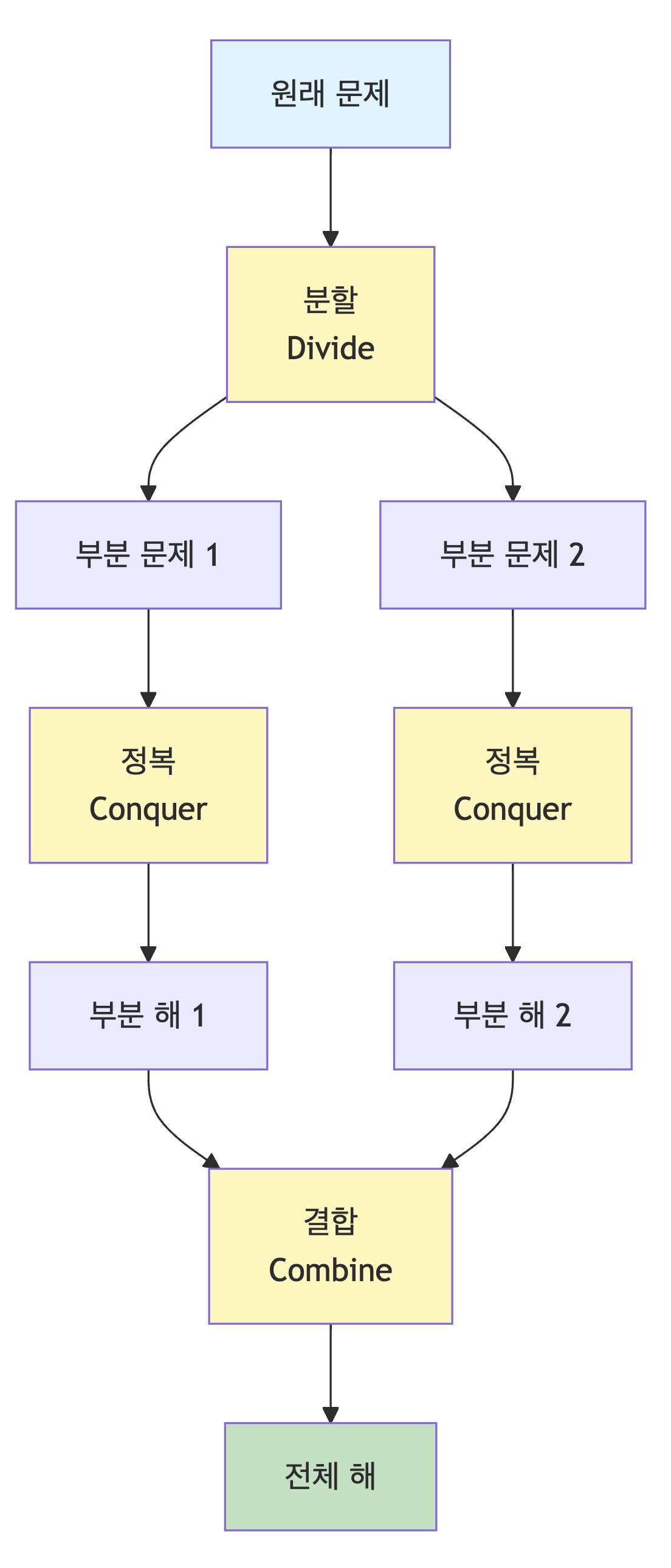
분할 정복의 기본 개념

분할

• 원래 문제를 더 이상 분할할 수 없을 때까지 작은 하위 문제들로 나눔
• 일반적으로 문제를 절반으로 나누는 방식을 많이 사용함
• 분할된 각 문제는 원래 문제와 같은 형태를 가짐

정복

• 분할된 각 하위 문제를 재귀적으로 해결함
• 문제의 크기가 충분히 작으면 직접 해결함 (기저 조건)
• 재귀 호출을 통해 더 작은 문제로 계속 분할함

결합

• 하위 문제들의 해결책을 모아서 원래 문제의 최종 해를 구함
• 부분 해들을 통합하여 전체 문제의 답을 도출함
• 경우에 따라 결합 단계가 매우 간단하거나 필요 없을 수도 있음

분할 정복의 조건

분할 정복이 효과적으로 동작하려면 다음 조건들이 충족되어야 함

부분 문제의 독립성

• 분할된 부분 문제들이 서로 독립적이어야 함
• 한 부분 문제의 해결이 다른 부분 문제에 영향을 주지 않아야 함
• 각 부분 문제를 독립적으로 해결할 수 있어야 병렬 처리가 가능함

같은 형태의 문제

• 분할된 작은 문제가 원래 문제와 같은 형태를 가져야 함
• 이것이 재귀 호출을 가능하게 함
• 동일한 알고리즘을 반복적으로 적용할 수 있어야 함

기저 조건의 존재

• 재귀를 종료할 수 있는 명확한 기저 조건(base case)이 있어야 함
• 문제가 충분히 작아졌을 때 직접 해결할 수 있어야 함
• 기저 조건이 없으면 무한 재귀에 빠질 수 있음

분할 정복 vs 동적계획법

• 분할 정복과 동적계획법은 자주 혼동되지만 중요한 차이가 있음

항목	분할 정복	동적계획법
부분 문제 특성	부분 문제들이 독립적임	부분 문제들이 겹침
중복 계산	중복 계산 발생 가능	메모이제이션으로 중복 제거
구현 방식	주로 재귀 방식	반복문 또는 재귀 + 메모이제이션
활용 분야	정렬, 탐색 알고리즘	최적화 문제, 최단 경로
예시	병합 정렬, 퀵 정렬, 이진 탐색	피보나치 수열, 배낭 문제
시간 복잡도	일반적으로 $O(n \log n)$	일반적으로 $O(n^2)$ 또는 $O(n)$

• 분할 정복
  • 부분 문제들이 중복되지 않으므로 각각을 한 번씩만 해결함
• 동적계획법
  • 부분 문제들이 중복되므로 한 번 계산한 결과를 저장하여 재사용함

분할 정복의 장점

빠른 속도

• 큰 문제를 작은 문제들로 분할하여 전체 실행 시간을 크게 줄일 수 있음
• 대부분 $O(n \log n)$의 시간 복잡도를 가져 효율적임
• $O(n^2)$보다 훨씬 빠른 성능을 제공함

쉬운 병렬화

• 분할된 부분 문제들이 독립적이므로 멀티코어 시스템에서 병렬 처리가 가능함
• 병렬 처리를 통해 성능을 크게 향상시킬 수 있음
• 대규모 데이터 처리에 유리함

유연성

• 여러 응용 분야에서 사용 가능함
• 문제의 복잡도와 데이터 크기와 무관하게 적용할 수 있음
• 다양한 문제에 동일한 패러다임을 적용할 수 있음

명확한 문제 해결 전략

• 문제를 분할하고 각각 해결하는 방식이 명확함
• 문제 해결 과정이 단순화됨
• 재귀적 구조로 인해 코드가 간결하고 이해하기 쉬움

분할 정복의 시간 복잡도 분석

마스터 정리

• 분할 정복의 시간 복잡도는 마스터 정리를 사용하여 계산함

• 일반적인 재귀 관계식

  \[T(n) = aT(n/b) + f(n)\]
  • $a$
    • 분할 후 생기는 부분 문제의 개수
  • $b$
    • 문제를 나누는 비율
  • $f(n)$
    • 분할과 결합에 소요되는 시간
• 병합 정렬
  • $T(n) = 2T(n/2) + O(n)$
    • 두 개의 부분 문제로 분할 ($a = 2$)
    • 각 부분은 절반 크기 ($b = 2$)
    • 병합에 $O(n)$ 시간 소요
    • 최종 시간 복잡도
      • $O(n \log n)$
• 이진 탐색
  • $T(n) = T(n/2) + O(1)$
    • 한 개의 부분 문제만 해결 ($a = 1$)
    • 절반으로 분할 ($b = 2$)
    • 비교에 $O(1)$ 시간 소요
    • 최종 시간 복잡도
      • $O(\log n)$

병합 정렬

• 병합 정렬은 분할 정복을 가장 잘 보여주는 대표적인 예임

동작 원리

• 배열을 중간에서 쪼개 비슷한 크기의 두 배열로 분할
• 각 배열을 재귀적으로 정렬 (정복)
• 정렬된 두 배열을 병합하여 최종 정렬된 배열 생성 (결합)

재귀 트리 구조

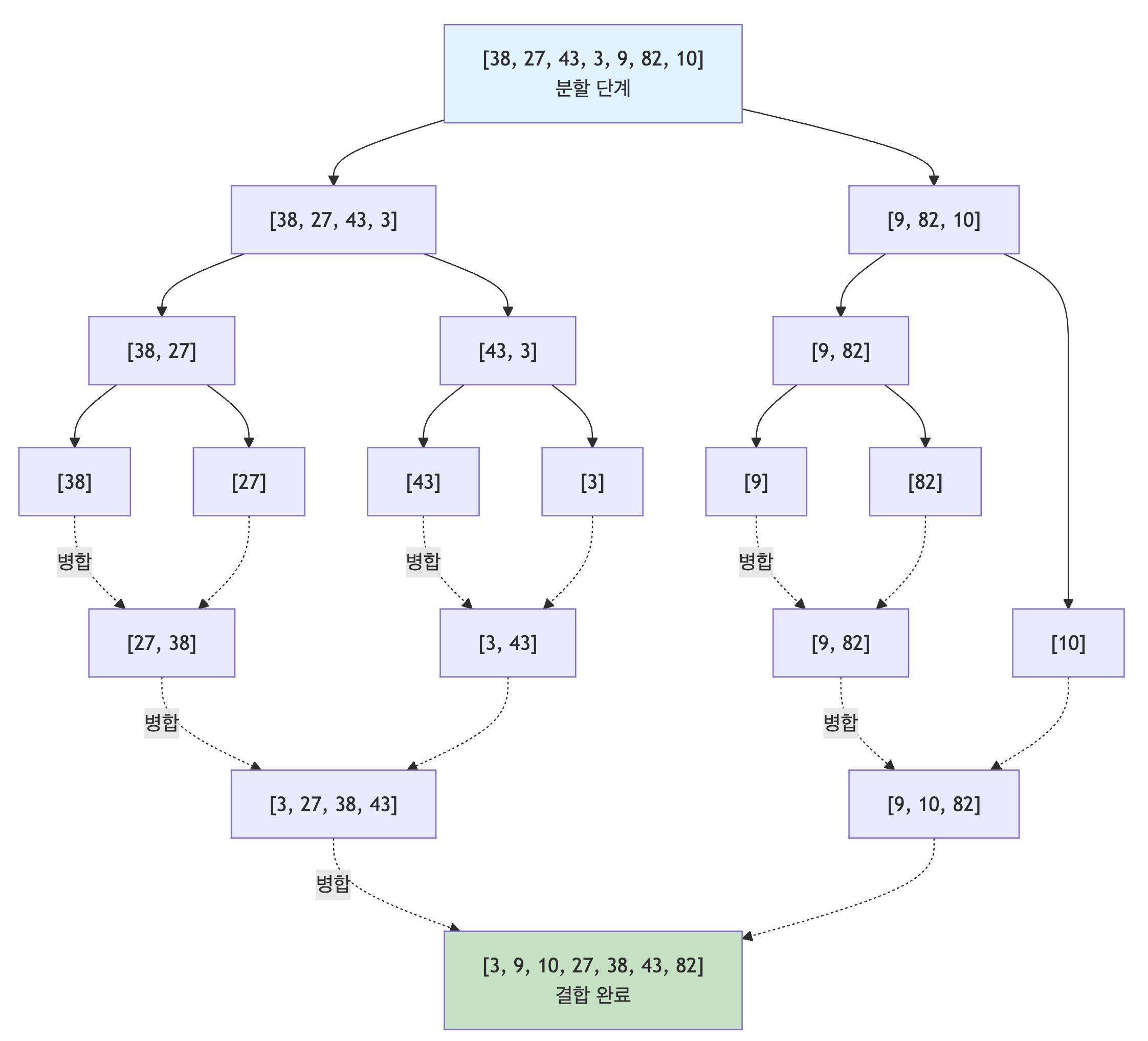
특징

• 각 단계마다 반으로 나눈 부분 문제를 처리한 후 결과를 합쳐서 원래 문제의 답을 계산함
• 시간 복잡도
  • $O(n \log n)$ (모든 경우)
• 공간 복잡도
  • $O(n)$ (추가 메모리 필요 - In-place가 아님)
• 안정한 정렬 알고리즘임

void mergeSort(int[] array, int left, int right) {
    if (left < right) {
        int mid = (left + right) / 2;
        
        // 분할 (Divide)
        mergeSort(array, left, mid);
        mergeSort(array, mid + 1, right);
        
        // 결합 (Combine)
        merge(array, left, mid, right);
    }
}

void merge(int[] array, int left, int mid, int right) {
    // 임시 배열 생성
    int[] temp = new int[right - left + 1];
    int i = left, j = mid + 1, k = 0;
    
    // 두 부분 배열을 비교하며 병합
    while (i <= mid && j <= right) {
        if (array[i] <= array[j]) {
            temp[k++] = array[i++];
        } else {
            temp[k++] = array[j++];
        }
    }
    
    // 남은 요소 복사
    while (i <= mid) temp[k++] = array[i++];
    while (j <= right) temp[k++] = array[j++];
    
    // 원본 배열에 복사
    System.arraycopy(temp, 0, array, left, temp.length);
}

퀵 정렬

• 퀵 정렬도 분할 정복을 사용하지만, 병합 정렬과는 다른 방식을 취함

동작 원리

• 피벗(pivot)이라는 기준값을 선택
• 피벗을 기준으로 배열을 두 부분으로 분할 (분할 단계에서 대부분의 작업 수행)
• 각 부분을 재귀적으로 정렬
• 결합 단계는 거의 아무것도 하지 않음

병합 정렬과의 차이

• 병합 정렬
  • 분할: 단순히 중간에서 나눔 (간단)
  • 결합: 두 정렬된 배열을 병합 (복잡)

퀵 정렬

• 분할: 피벗 기준으로 요소들을 재배치 (복잡)
• 결합: 아무것도 하지 않음 (간단)

특징

• 모든 중요한 작업이 분할 단계에서 일어남
• 파티션 과정에는 주어진 수열의 길이에 비례하는 시간이 소요됨
• 시간 복잡도
  • 평균: $O(n \log n)$
  • 최악: $O(n^2)$ (피벗을 잘못 선택했을 때 - 이미 정렬된 배열에서 첫 번째나 마지막 요소를 피벗으로 선택한 경우 등)
• 공간 복잡도
  • $O(\log n)$ (재귀 스택, In-place 정렬 가능)

void quickSort(int[] array, int left, int right) {
    if (left < right) {
        // 분할 (Divide) - 여기서 대부분의 작업 수행
        int pivot = partition(array, left, right);
        
        // 정복 (Conquer)
        quickSort(array, left, pivot - 1);
        quickSort(array, pivot + 1, right);
        
        // 결합 (Combine) - 아무것도 하지 않음
    }
}

int partition(int[] array, int left, int right) {
    int pivot = array[right];
    int i = left - 1;
    
    // 피벗보다 작은 요소는 왼쪽으로
    for (int j = left; j < right; j++) {
        if (array[j] < pivot) {
            i++;
            swap(array, i, j);
        }
    }
    
    // 피벗을 중간 위치로 이동
    swap(array, i + 1, right);
    return i + 1;
}

void swap(int[] array, int i, int j) {
    int temp = array[i];
    array[i] = array[j];
    array[j] = temp;
}

이진 탐색

• 이진 탐색도 분할 정복 기법을 활용함

동작 원리

• 정렬된 배열을 반으로 나눔 (분할)
• 찾으려는 값이 어느 절반에 위치하는지 확인 (정복)
• 해당 절반에서 다시 같은 과정을 반복
• 결합 단계는 필요 없음 (값을 찾거나 못 찾거나)

특징

• 시간 복잡도
  • $O(\log n)$
• 공간 복잡도
  • $O(1)$ (반복문)
  • $O(\log n)$ (재귀)
• 반드시 정렬된 배열에서만 사용 가능함

// 재귀 방식
int binarySearch(int[] array, int target) {
    return binarySearchHelper(array, target, 0, array.length - 1);
}

int binarySearchHelper(int[] array, int target, int left, int right) {
    // 기저 조건: 찾지 못한 경우
    if (left > right) return -1;
    
    // 분할: 중간 인덱스 계산
    int mid = left + (right - left) / 2;
    
    // 정복: 찾은 경우
    if (array[mid] == target) return mid;
    
    // 정복: 왼쪽 절반 탐색
    if (array[mid] > target) {
        return binarySearchHelper(array, target, left, mid - 1);
    }
    
    // 정복: 오른쪽 절반 탐색
    return binarySearchHelper(array, target, mid + 1, right);
}

// 반복문 방식 (더 효율적)
int binarySearchIterative(int[] array, int target) {
    int left = 0, right = array.length - 1;
    
    while (left <= right) {
        int mid = left + (right - left) / 2;
        
        if (array[mid] == target) {
            return mid;
        } else if (array[mid] > target) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    
    return -1;  // 찾지 못함
}

거듭제곱 연산

• 큰 수의 거듭제곱을 계산할 때도 분할 정복을 사용함

동작 원리

• $n^{100}$을 계산할 때
  • 일반적인 방법
    • $n$을 100번 곱함 → $O(n)$
  • 분할 정복
    • $n^{100} = n^{50} \times n^{50}$ → $O(\log n)$

특징

• 시간 복잡도
  • $O(\log n)$
• 곱셈 횟수를 크게 줄일 수 있음

// 재귀 방식
long power(long base, int exp) {
    // 기저 조건
    if (exp == 0) return 1;
    if (exp == 1) return base;
    
    // 분할: 지수를 절반으로
    long half = power(base, exp / 2);
    
    // 결합: 절반 결과를 제곱
    if (exp % 2 == 0) {
        return half * half;
    } else {
        return half * half * base;
    }
}

최대 부분 배열 합

• 배열에서 연속된 요소들의 최대 합을 구하는 문제

동작 원리

• 배열을 반으로 나눔
• 왼쪽 절반의 최대 부분 배열 합 계산
• 오른쪽 절반의 최대 부분 배열 합 계산
• 중간을 가로지르는 최대 부분 배열 합 계산
• 세 값 중 최댓값 반환

특징

• 시간 복잡도
  • $O(n \log n)$
• 카데인 알고리즘($O(n)$)보다는 느리지만, 분할 정복 개념을 잘 보여주는 예시임

int maxSubarraySum(int[] array, int left, int right) {
    // 기저 조건: 요소가 하나만 있을 때
    if (left == right) {
        return array[left];
    }
    
    int mid = (left + right) / 2;
    
    // 분할 정복
    int leftMax = maxSubarraySum(array, left, mid);
    int rightMax = maxSubarraySum(array, mid + 1, right);
    int crossMax = maxCrossingSum(array, left, mid, right);
    
    // 결합: 세 값 중 최댓값 반환
    return Math.max(Math.max(leftMax, rightMax), crossMax);
}

int maxCrossingSum(int[] array, int left, int mid, int right) {
    // 중간에서 왼쪽으로 최대 합
    int sum = 0;
    int leftSum = Integer.MIN_VALUE;
    for (int i = mid; i >= left; i--) {
        sum += array[i];
        leftSum = Math.max(leftSum, sum);
    }
    
    // 중간에서 오른쪽으로 최대 합
    sum = 0;
    int rightSum = Integer.MIN_VALUE;
    for (int i = mid + 1; i <= right; i++) {
        sum += array[i];
        rightSum = Math.max(rightSum, sum);
    }
    
    return leftSum + rightSum;
}

분할 정복 구현 시 주의사항

기저 조건 명확히 설정

• 재귀가 언제 멈춰야 할지 명확하게 정의해야 함
• 기저 조건이 없으면 무한 재귀에 빠질 수 있음
• 문제가 충분히 작아졌을 때의 직접 해결 방법을 정의해야 함

// 나쁜 예: 기저 조건 누락
void badRecursion(int n) {
    if (n == 0) return;  // n이 음수가 되면?
    badRecursion(n - 1);
}

// 좋은 예: 명확한 기저 조건
void goodRecursion(int n) {
    if (n <= 0) return;  // 음수도 처리
    goodRecursion(n - 1);
}

부분 문제의 크기 감소 확인

• 재귀 호출 시 부분 문제의 크기가 계속 감소해야 함
• 크기가 감소하지 않으면 무한 루프에 빠질 수 있음

// 나쁜 예: 크기가 감소하지 않음
void badDivide(int[] array, int left, int right) {
    if (left >= right) return;
    badDivide(array, left, right);  // 크기가 그대로!
}

// 좋은 예: 크기가 감소함
void goodDivide(int[] array, int left, int right) {
    if (left >= right) return;
    int mid = (left + right) / 2;
    goodDivide(array, left, mid);      // 크기 감소
    goodDivide(array, mid + 1, right); // 크기 감소
}

스택 오버플로우 방지

• 깊은 재귀 호출로 인한 스택 오버플로우를 고려해야 함
• 필요시 반복문으로 변환하거나 꼬리 재귀 최적화를 고려함

// 재귀 깊이가 너무 깊을 수 있음
int factorial(int n) {
    if (n <= 1) return 1;
    return n * factorial(n - 1);  // O(n) 스택 공간
}

// 반복문으로 변환
int factorialIterative(int n) {
    int result = 1;
    for (int i = 2; i <= n; i++) {
        result *= i;
    }
    return result;  // O(1) 스택 공간
}

시간 복잡도 정확히 분석

• 마스터 정리를 사용하여 시간 복잡도를 정확히 분석해야 함
• 분할 횟수와 각 단계의 작업량을 고려해야 함

정리

• 분할 정복은 큰 문제를 작은 부분 문제로 나누어 해결한 후 결합하는 알고리즘 설계 패러다임임
• 분할(Divide), 정복(Conquer), 결합(Combine)의 세 단계로 구성됨
• 동적계획법과 달리 부분 문제들이 독립적이어서 중복 계산이 발생하지 않음
• 대표적인 예시로 병합 정렬($O(n \log n)$), 퀵 정렬(평균 $O(n \log n)$), 이진 탐색($O(\log n)$)이 있음

Reference

• Do it! 알고리즘 코딩 테스트 - 자바 편