학습 개요
- 데이터 표현이라는 관점에서 컴퓨터 내부에서 데이터를 어떻게 표현하는 지에 대해서 살펴봄
- 데이터와 정보의 개념적인 차이를 이해하고, 정수와 실수, 그리고 문자 표현과 관련된 다양한 개념과 방법들을 학습함
학습 목표
- 데이터와 정보의 개념적 차이, 그리고 데이터 표현 단위 등을 이해하고 설명할 수 있음
- 다양한 진법 간의 변환을 수행할 수 있음
- 정수와 실수의 표현 방법을 이해하고 설명할 수 있음
- 문자 표현의 개념과 문자 코드의 종류를 이해하고 설명할 수 있음
강의록
데이터와 정보
데이터와 정보의 관계
-
I = P(D)
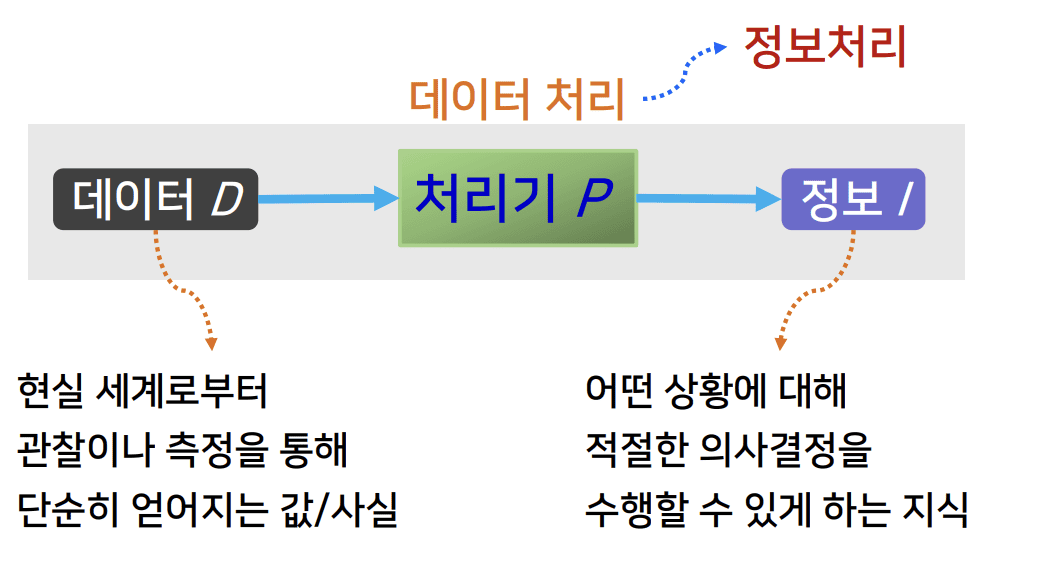
- 데이터
- 현실 세계로부터 관찰이나 측정을 통해 단순히 얻어지는 값/사실
- 정보
- 어떤 상황에 대해 적절한 의사 결정을 수행할 수 있게 하는 지식
데이터의 표현 형태
- 데이터의 유형과 무관하게 일관된 표현 방식 사용
- 문자, 정수/실수, 이미지, 오디오, 비디오 등
- 비트 패턴
- 메모리에 저장된 데이터 유형에 맞는 해석과 처리가 필요
- 입출력 장치나 프로그램의 책임/역할
- 문자, 정수/실수, 이미지, 오디오, 비디오 등
데이터의 표현 단위
-
비트(binaryd digit)

-
바이트(byte)

- KB(2¹⁰≈10³), MB(2²⁰≈10⁶), GB(2³⁰≈10⁹), TB(2⁴⁰≈10¹²), PB(2⁵⁰≈10¹⁵), EB(2⁶⁰≈10¹⁸), ZB(2⁷⁰≈10²¹), YB(2⁸⁰≈10²⁴)
- 워드(word)
- 컴퓨터 연산의 기본 단위가 되는 정보의 양
- 보통 32 bit, 64 bit
진법
진법(number system)
- 수를 세는 방법 또는 단위
- r 진법
- 0, 1, ⋯, (r - 1)까지의 숫자만을 사용하는 진법
- r 진수
- 0, 1, ⋯, (r - 1)까지의 숫자만을 사용하는 진법
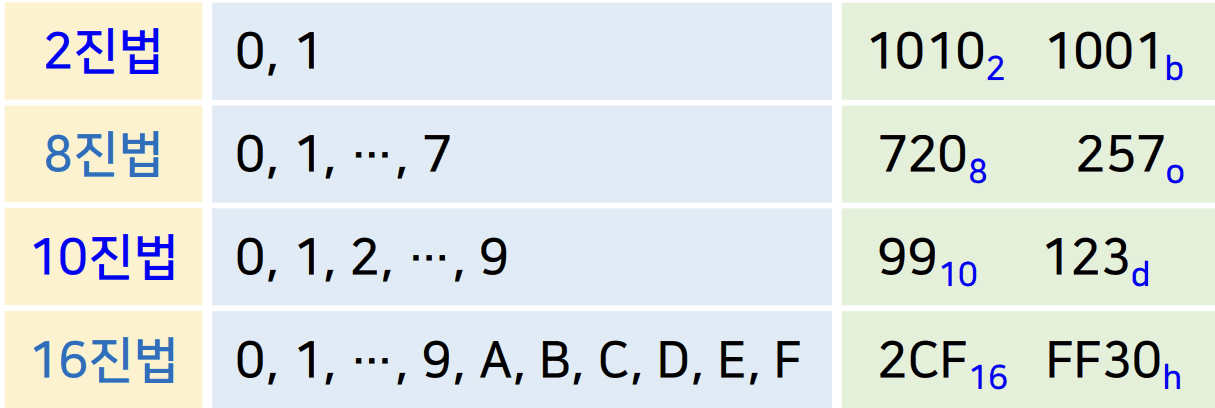
- r 진법
- 진법의 각 숫자는 위치에 따른 서로 다른 가중치(자릿 값)를 가짐
- r 진법의 자릿 값
- rˣ
- x는 숫자의 위치를 나타내는 정수
- rˣ

- r 진법의 자릿 값
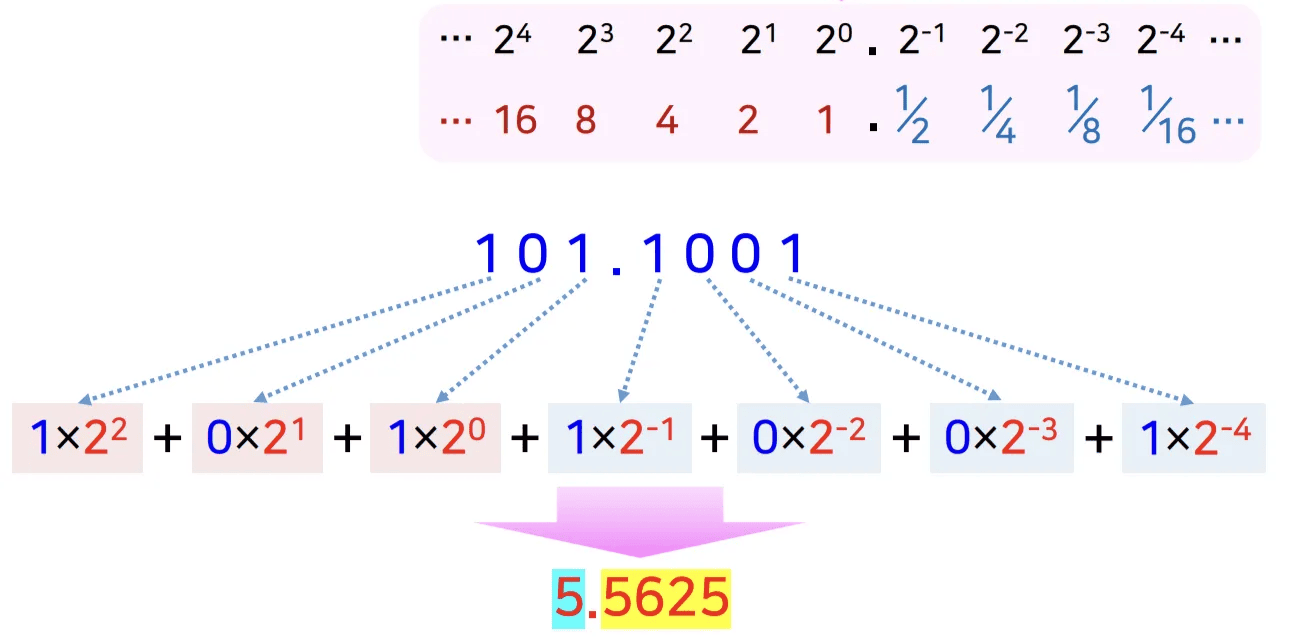
2진수를 10진수로 변환
-
10진수 = ∑(각 비트 값 * 해당 비트 위치의 가중치)
8/16진수를 10진수로 변환
-
10진수 = ∑(각 숫자 값 * 해당 위치의 가중치)

10진수를 r진수로 변환(r = 2, 8, 16)
-
정수 부분과 소수 부분을 구분하여 각각의 방법으로 처리한 후, 각 결과를 단순히 연결해서 나열
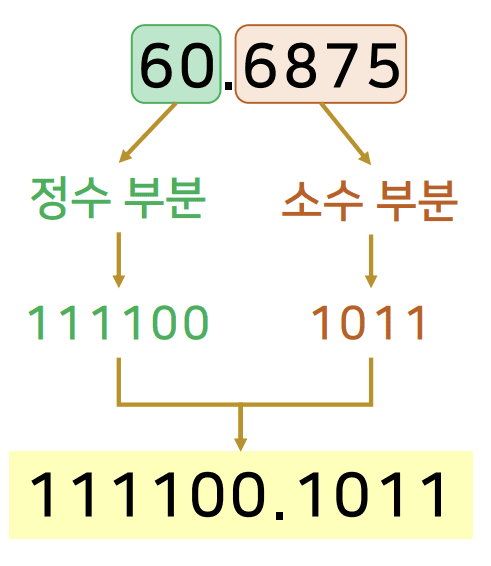
- 정수 60
- 60 % 2 = 0
- 30 % 2 = 0
- 15 % 2 = 1
- 7 % 2 = 1
- 3 % 2 = 1
- 1 % 2 = 1
- 소수 6875
- 0.6875 * 2 = 1.375
- 0.375 * 2 = 0.75
- 0.75 * 2 = 1.5
- 0.5 * 2 = 1.0
- 정수 60
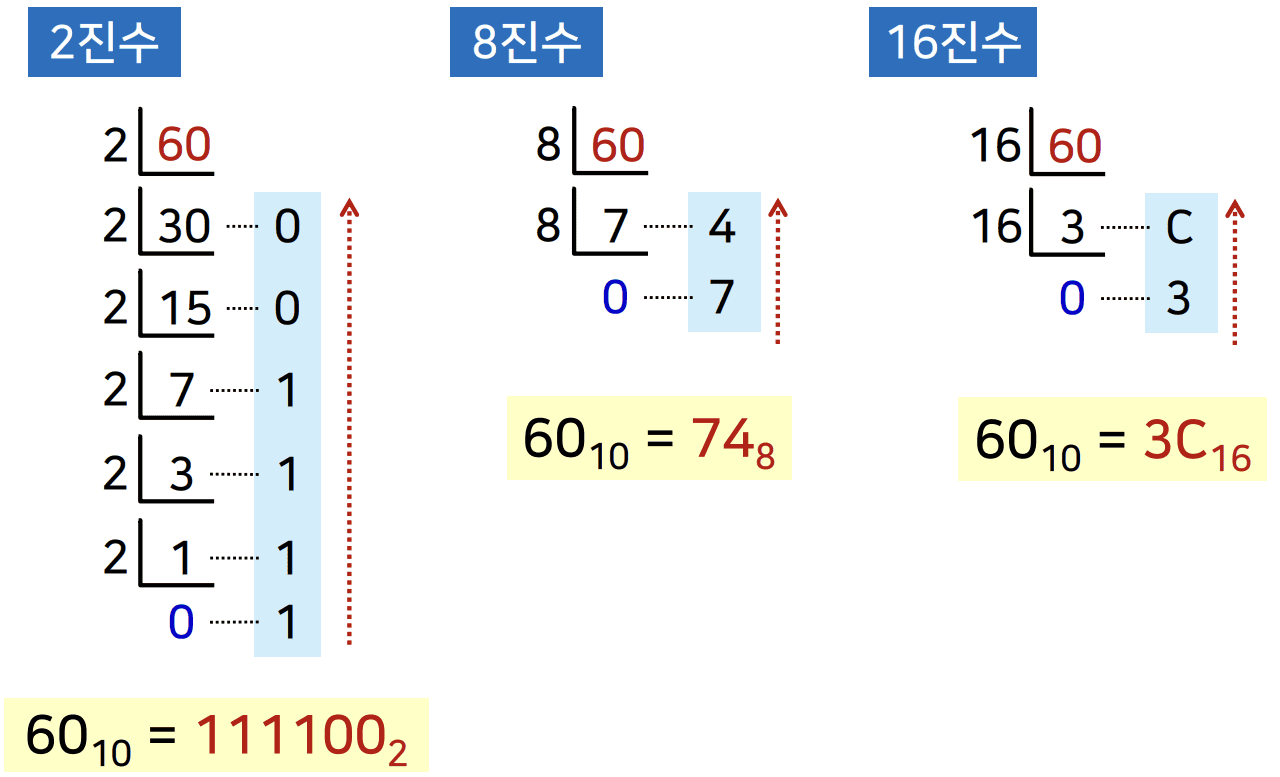
10진수_정수 부분 → r 진수
-
알고리즘
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
입력값 = 10진수(정수 부분); // 변환하고 싶은 10진수 정수 i = 0; 몫 = 입력값 / r; // 몫은 정수 부분만 나머지 = 입력값 mod(%) r; // 나머지는 입력값에서 r을 나눈 나머지 값을 가짐 결과(i) = 나머지; // 순서대로 기록 while (몫 ≠ 0) 입력값 = 몫; // 나눠진 결과를 몫으로 i = i+1; // 자리 하나 증가 몫 = 입력값 / r; 나머지 = 입력값 mod r; 결과(i) = 나머지 end 출력[결과(i), 결과(i- 1), …, 결과(0)]; // 나머지를 역순으로 나열- 몫과 나머지(%)를 반복해서 구함
- 나머지는 결과 배열에 차곡차곡 쌓음
- 반복 종료 후, 결과를 거꾸로 읽어주면 원하는 진법의 수가 됨
10진수_소수 부분 → r 진수 (r = 2, 6, 18)
-
알고리즘
1 2 3 4 5 6 7 8 9 10 11
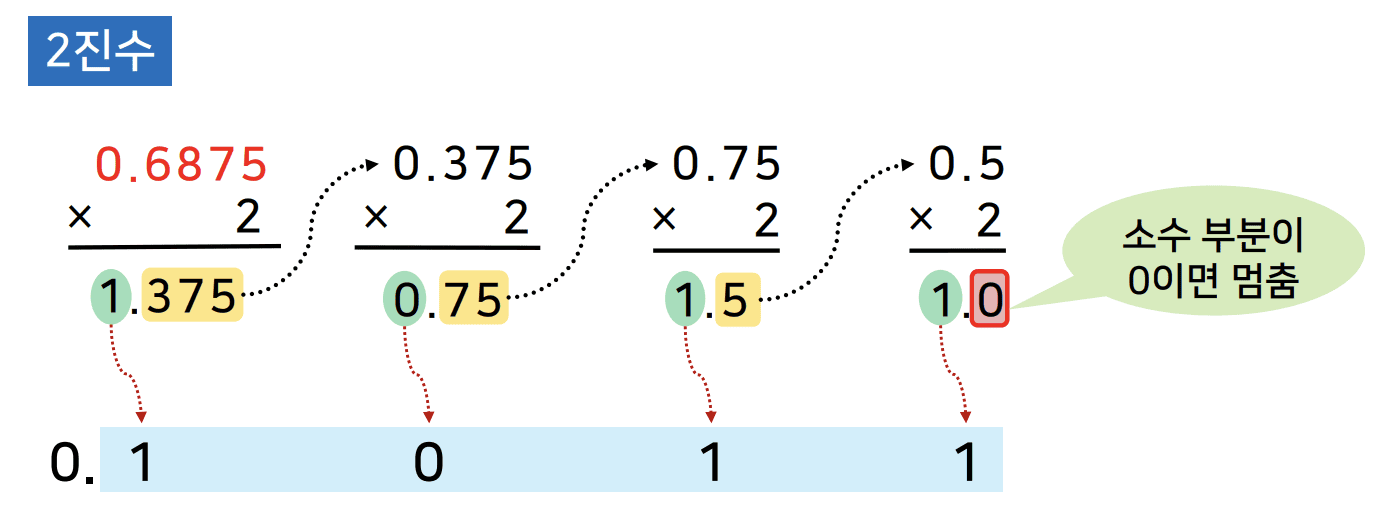
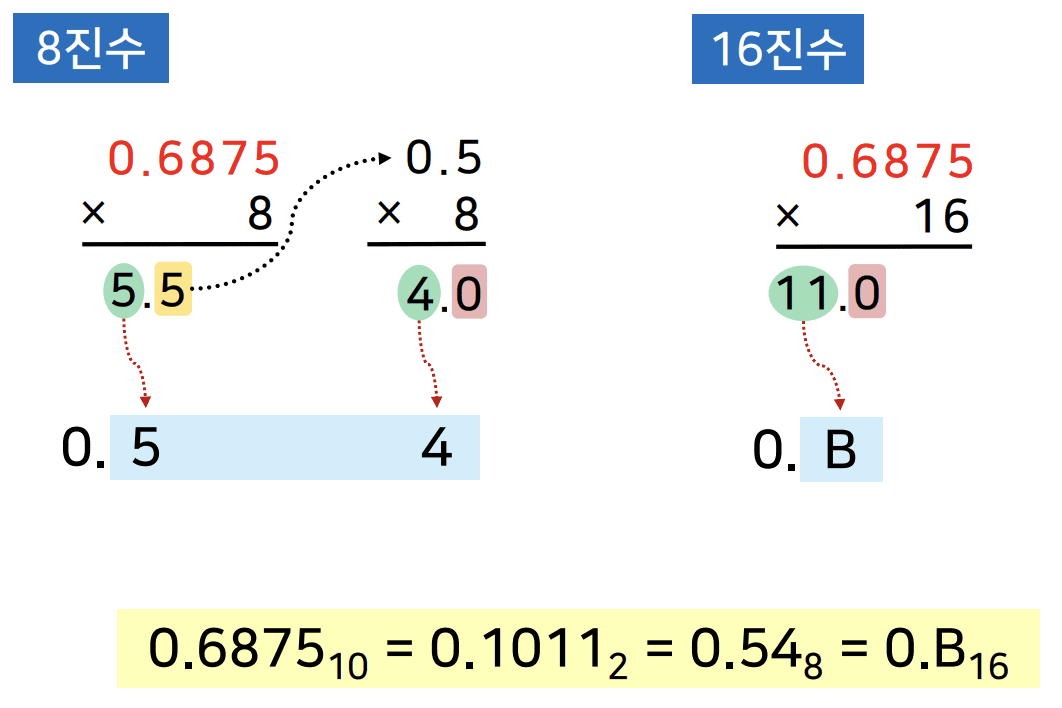
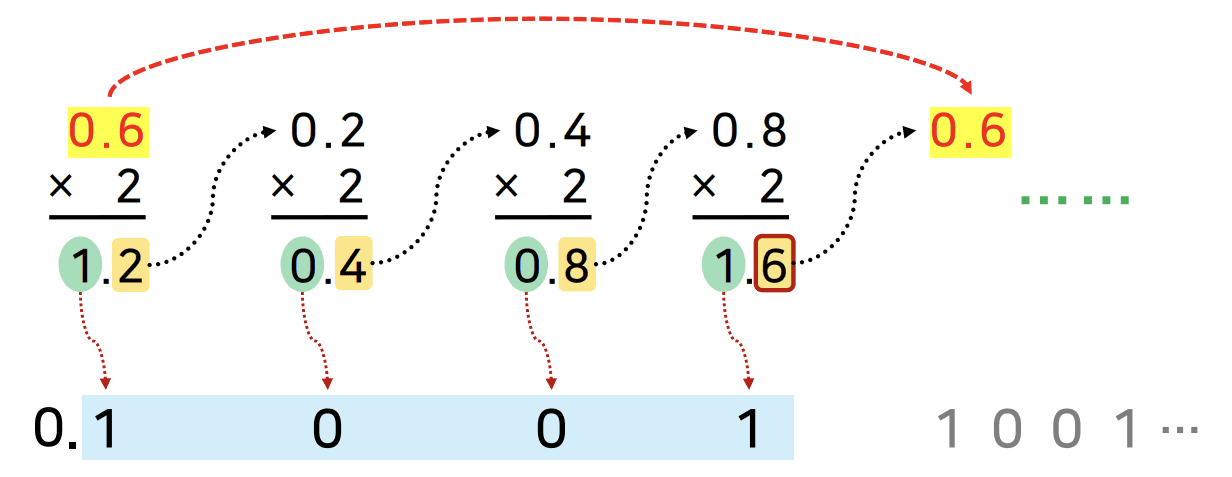
입력값 = 10진수(소수 부분); // 변환하고 싶은 10진수 소수 부분만 출력 i = 0; while (입력값 ≠ 0) 임시변수 = 입력값 * r; 결과(i) = 임시변수의 정수 부분; // 곱한 값의 정수 부분 i = i + 1; 입력값 = 임시변수의 소수 부분; // 곱한 값의 소수 부분은 다음 단계의 입력 end 출력[0.결과(0), 결과(1), …, 결과(i)];- 10진수 소수 부분 × 진법(r)
- 곱한 결과의 정수 부분을 진법 소수점 아래에 기록
- 곱한 결과의 소수 부분을 다음 단계에서 다시 x r
- 반복 후, 차례대로 기록한 값이 r진수의 소수점 아래 자리 수가 됨
r 진수 간의 변환(r = 2, 8, 16)
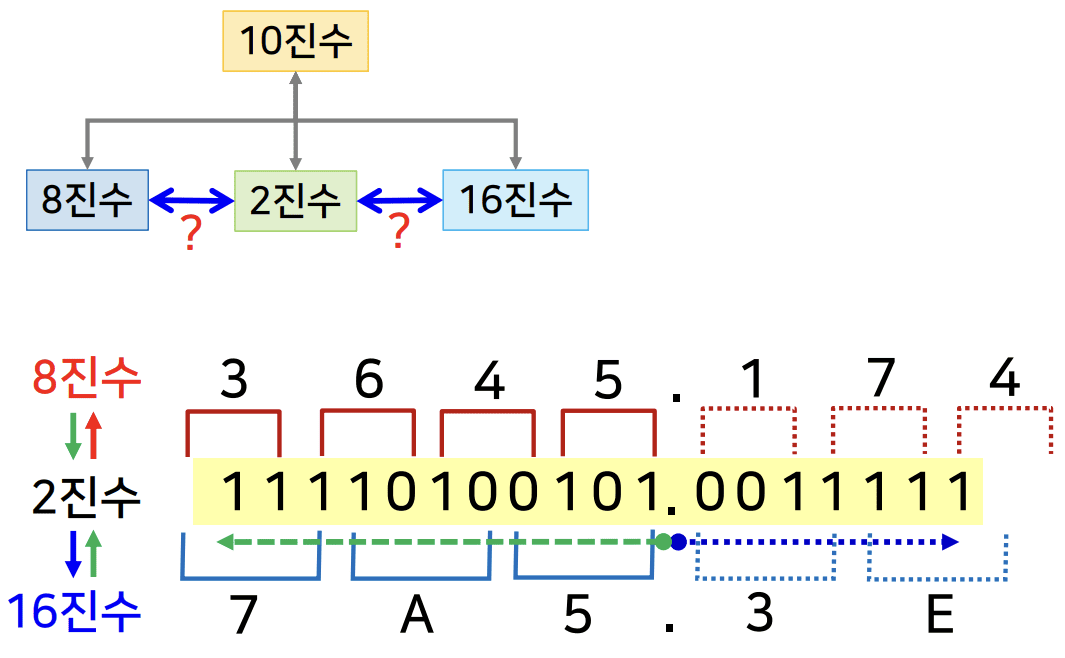
- 2진수의 3 자릿수 = 8진수의 1 자릿수
- 2진수의 4 자릿수 = 16진수의 1 자릿수
정수 표현
정수 표현 방법
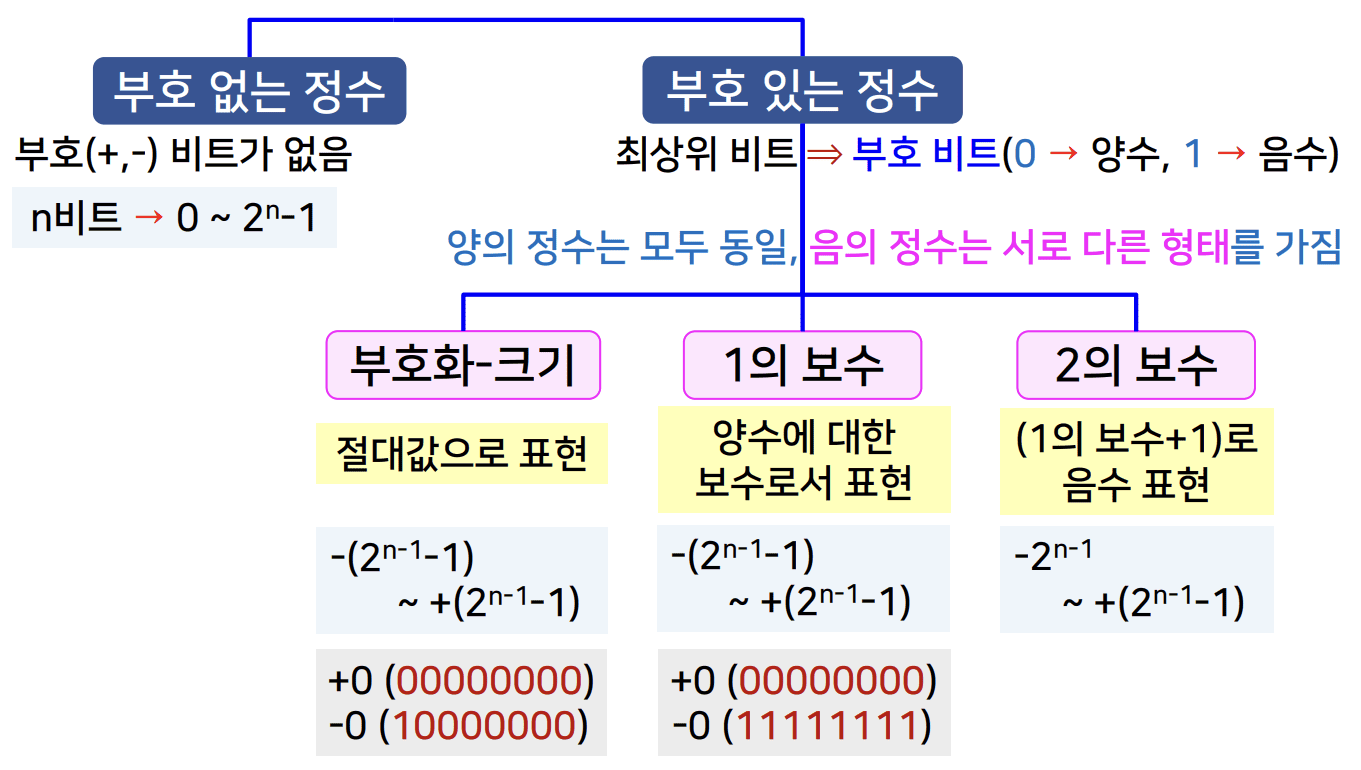
- 부호 없는 정수
- 부호(+, -) 비트 미존재
- n비트 → 0 ~ 2ⁿ - 1
- 부호 있는 정수
- 최상위 비트 = 부호 비트 (0: 양수, 1: 음수)
- 양의 정수는 모두 동일, 음의 정수는 서로 다른 형태 가짐
- 부호화-크기
- 절대 값으로 표현
- -(2⁽ⁿ⁻¹⁾ - 1) ~ +(2⁽ⁿ⁻¹⁾ - 1)
- +0(00000000) -0(10000000)
- 1의 보수
- 양수에 대한 보수로서 표현
- -(2⁽ⁿ⁻¹⁾ - 1) ~ +(2⁽ⁿ⁻¹⁾ - 1)
- +0(00000000) -0(11111111)
- 2의 보수
- (1의 보수 + 1)로 음수 표현
- -2⁽ⁿ⁻¹⁾ ~ +(2⁽ⁿ⁻¹⁾ - 1)
부호 없는 정수
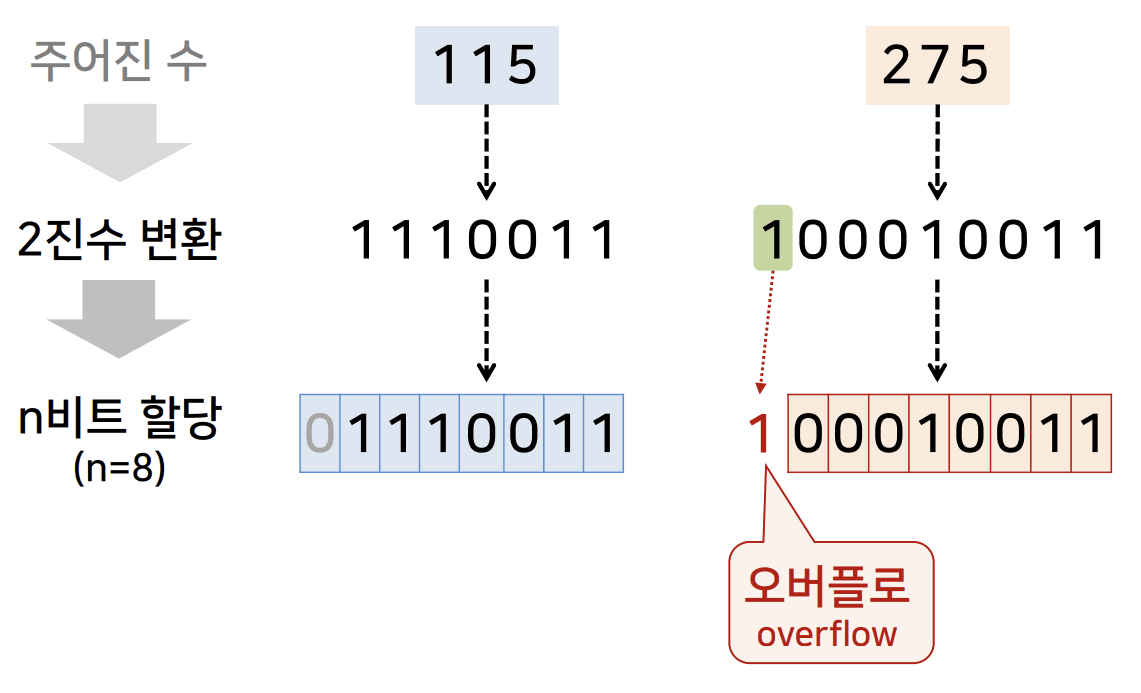
- 주어진 수 → 2진수 변환 → n 비트 할당(n = 8)
- 115 → 1110011 → 01110011
- 275 → 100010011 → 1/00010011 (overflow 발생)
부호 있는 정수
-
n = 8 비트인 경우
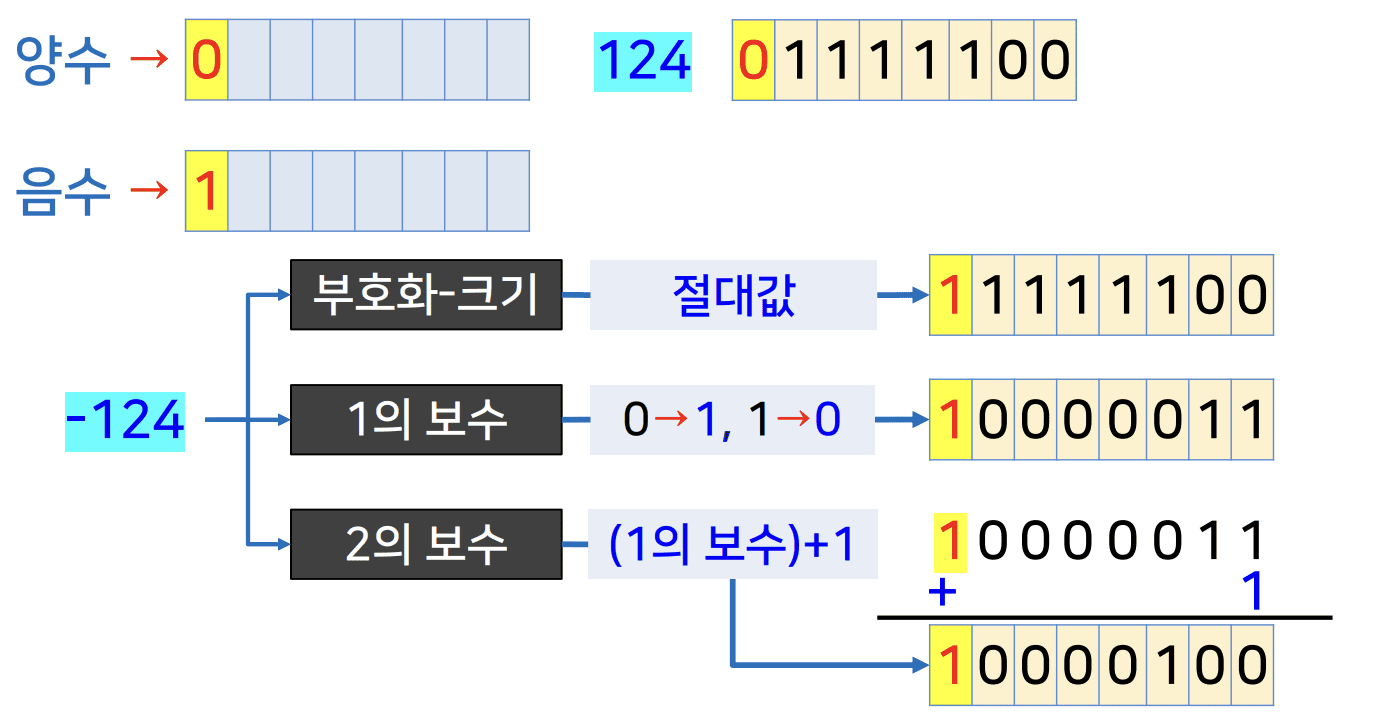
- 양수 : 0
- 음수 : 1
- 124 : 01111100
-
- 124
- 부호화-크기
- 절대 값
- 11111100
- 1의 보수
- 0 → 1, 1 → 0
- 1000011
- 2의 보수
- (1의 보수) + 1
- 1000011 + 1 = 1000100
- 부호화-크기
- 124
정수 표현 방법의 비교
| 이진 표현 | 부호 없는 정수 | 부호 있는 정수(부호화-크기) | 부호 있는 정수(1의 보수) | 부호 있는 정수(2의 보수) |
|---|---|---|---|---|
| 00000000 | 0 | +0 | +0 | +0 |
| 00000001 | 1 | +1 | +1 | +1 |
| 00000010 | 2 | +2 | +2 | +2 |
| 00000011 | 3 | +3 | +3 | +3 |
| … | … | … | … | … |
| 01111100 | 124 | +124 | +124 | +124 |
| 01111101 | 125 | +125 | +125 | +125 |
| 01111110 | 126 | +126 | +126 | +126 |
| 01111111 | 127 | +127 | +127 | +127 |
| 10000000 | 128 | -0 | - 127 | - 128 |
| 10000001 | 129 | - 1 | - 126 | - 127 |
| 10000010 | 130 | -2 | - 125 | - 126 |
| 10000011 | 131 | -3 | - 124 | - 125 |
| … | … | … | … | … |
| 11111100 | 252 | - 124 | -3 | -4 |
| 11111101 | 253 | - 125 | -2 | -3 |
| 11111110 | 254 | - 126 | - 1 | -2 |
| 11111111 | 255 | - 127 | -0 | - 1 |
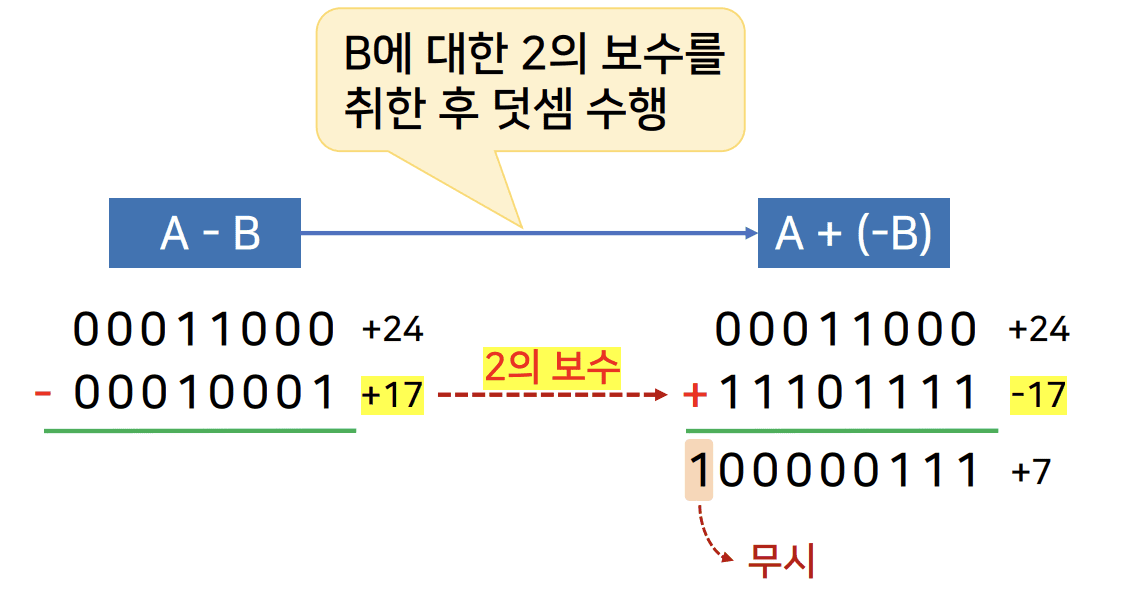
2의 보수 방식의 응용
- 뺄셈
- 24 - 17
- 이진수 10001100은 십진수로 얼마인가?
-
8비트, 2의 보수 방식
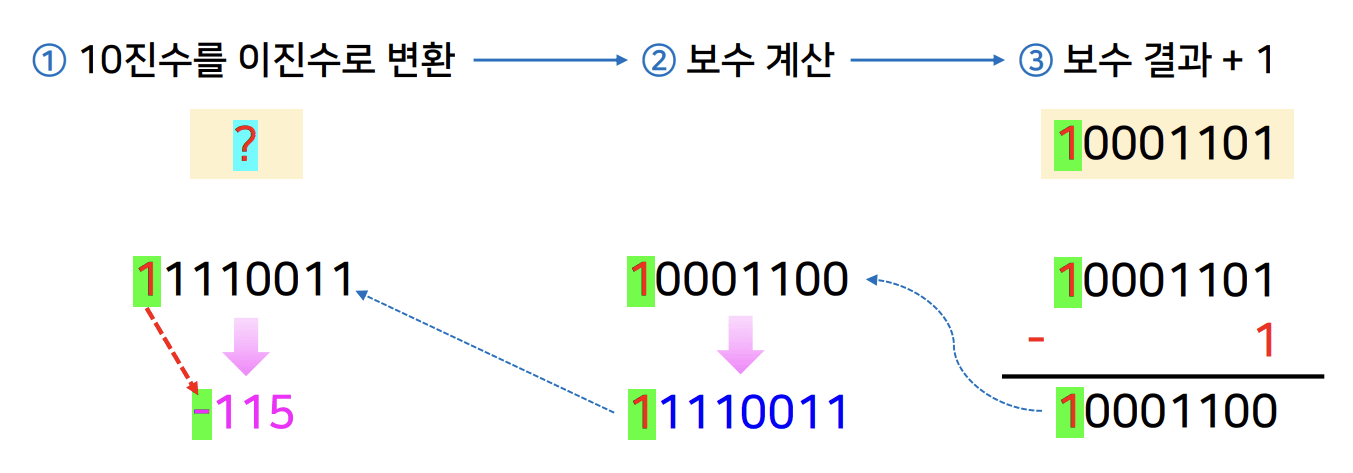
- 10001101 - 1 = 10001100
- 보수 계산
- 11110011
- 십진수 변환
- -115
-
실수 표현
실수 표현
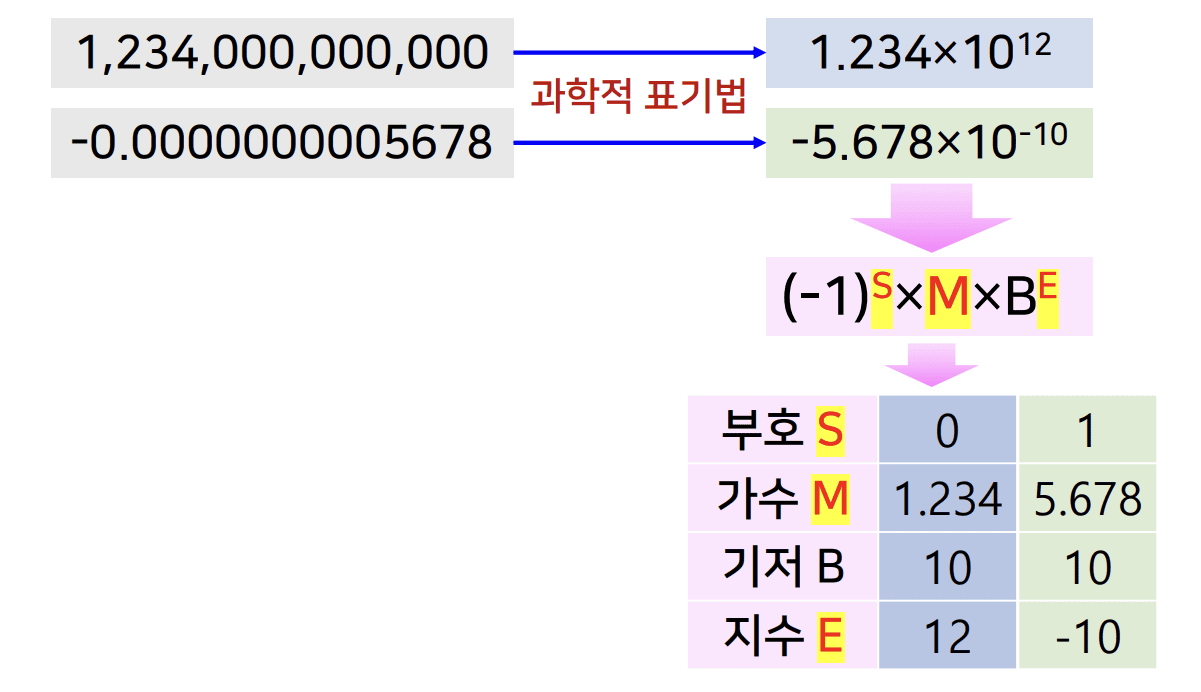
- 과학적 표기법을 활용한 부동 소수점 방식으로 표현
- 1,234,000,000,000 → 1.234 * 10¹²
- -0.0000000005678 → -5.678 * 10⁻¹⁰
-
(- 1)ˢ * M * Bᵉ
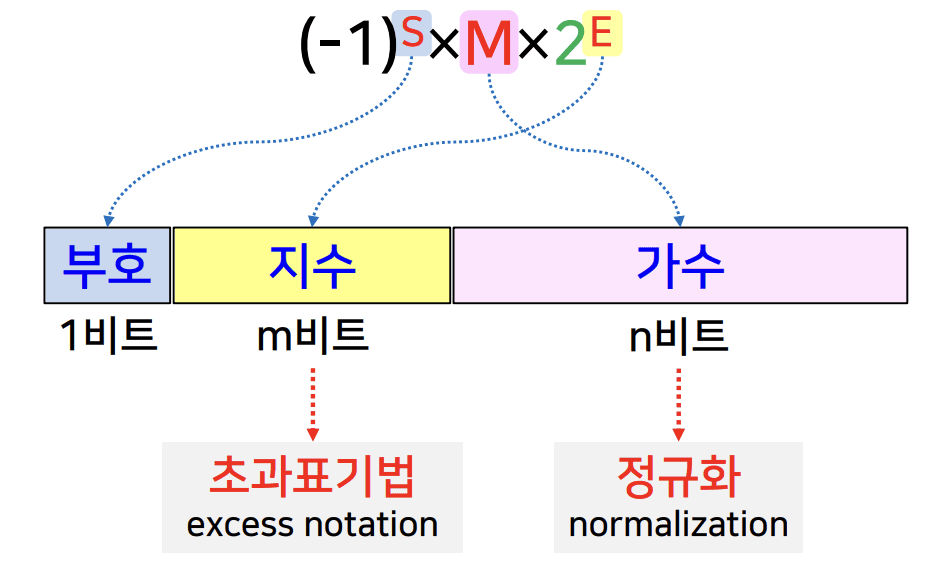
초과 표기법
- 부동 소수점 방식의 지수 부분의 표현만을 위한 정수 표현 방법
- 매직 넘버 → 지수 부분이 m 비트로 구성 → 2ᵐ⁻¹ 또는 2ᵐ⁻¹ - 1
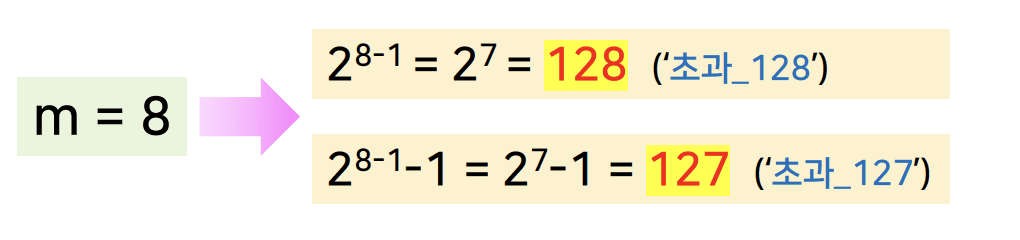

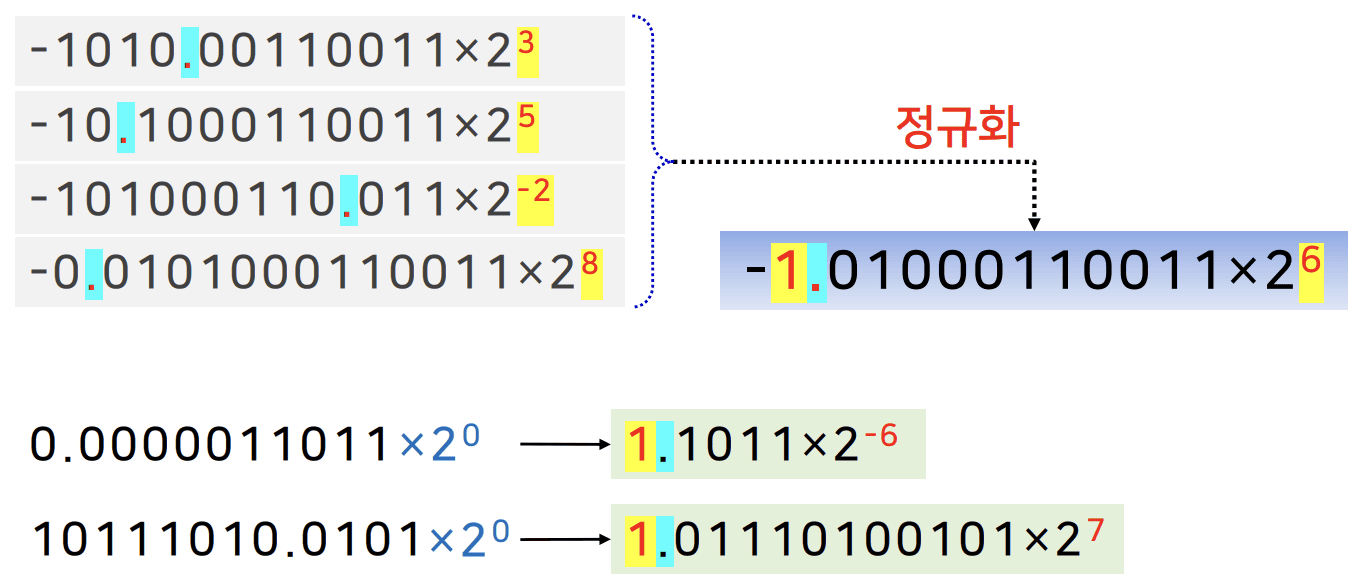
정규화
-
가수를 표현할 때 표준화 된 형식 필요
실수 표현의 예

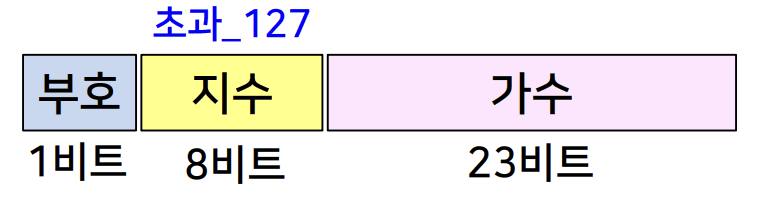
IEEE 부동 소수점 방식의 표준 형식
-
단정도(single precision) → 4 바이트
-
배정도(double precision) → 8 바이트

문자 표현
문자 표현
- 키보드를 통해 입력되는 문자는 내부적으로 2진수로 표현되어 처리
- 각 문자마다 유일한 값으로써 코드를 할당할 수 있는 약속된 문자 체계가 필요
- 문자 체계의 종류
- ASCII, 유니코드, …
- 문자 체계의 종류
ASCII
- American Standard Code for Information Interchange
- 미국 표준 협회(ANSI)
- 7비트 코드 → 128개(2⁷)의 서로 다른 문자 표현
- 확장된 아스키(Extended ASCII) → 1비트 + 7비트
- 1비트
- 0
- 패러티(parity) 비트
- 짝수 패러티 → 11001100
- 홀수 패러티 → 01001100
- 1비트
- 확장된 아스키(Extended ASCII) → 1비트 + 7비트
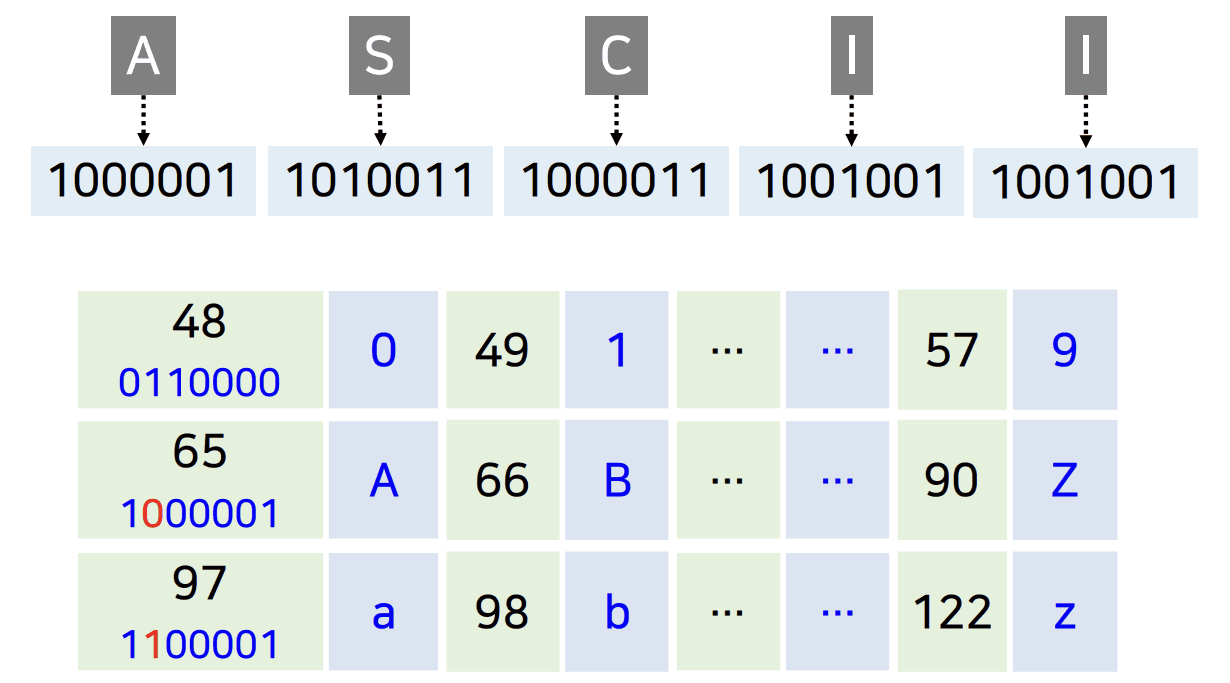
-
A(1000001) S(1010011) C(1000011) I(1001001) I(1001001)
유니코드
- 세계의 모든 문자를 컴퓨터에서 일관되게 표현하고 다룰 수 있도록 설계 된 표준
- 1990년 애플 컴퓨터, IBM, MS 등의 컨소시엄으로 설립한 유니코드(Unicode)가 첫 버전 발표
- 1995년 국제 표준으로 제정
- 공식 명칭: ISO/IC 10646- 1
- 사용 중인 플랫폼, 프로그램, 언어에 무관
- 16비트 코드 체계
- 65,636개(216)의 서로 다른 문자 표현
- 1995년 국제 표준으로 제정
- 1990년 애플 컴퓨터, IBM, MS 등의 컨소시엄으로 설립한 유니코드(Unicode)가 첫 버전 발표
기타 코드 체계
- EBCDIC(Extended Binary Coded Decimal Interchange Code)
- IBM 개발
- IBM 메인 프레임에서만 사용
- 8비트 코드
- 실제 사용되는 문자 코드는 128개
- IBM 개발
- BCD(Binary Coded Decimal)
- 4비트로 구성 된 10개의 코드로 10진수를 표현하는 방식
- 8421 코드
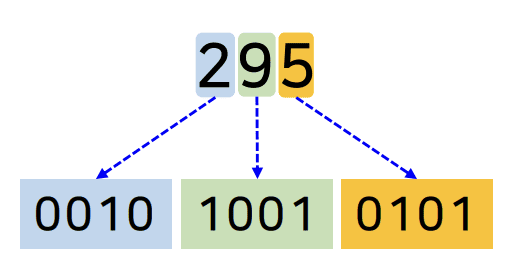
- 4비트로 구성 된 10개의 코드로 10진수를 표현하는 방식
정리 하기
- 데이터와 정보
- 정보 = P(데이터), 비트 패턴
- 데이터 표현 단위
- 비트, 바이트, KB, MB, GB, TB, PB, EB, ZB, YB, 워드
- 진법
- 변환
- 2/8/16진수 ↔ 10진수
- 8진수 ↔ 2진수 ↔ 16진수
- 변환
- 정수 표현
- 부호 없는 정수
- 부호 있는 정수
- 양수는 동일
- 음수 표현
- 부호화-크기
- 1의 보수
- 2의 보수
- 실수 표현
- (-1)ˢ * M * 2ᵉ
- 초과 표기 법
- 정규화
- 문자 표현
- ASCII
- 유니코드
연습 문제
-
주어진 여러 진법의 수 중에서 가장 작은 값을 나타내는 것은?
a. 0.43(8)
- 0.43(8) = 4 * 8⁻¹ + 3 * 8⁻² = 4 * 0.125 + 3 * 0.015625 = 0.546875(10)
- 0.98(16) = 9 * 16⁻¹ + 8 * 16⁻² = 9 * 0.062375 + 8 * 0.004 = 0.59375(10)
- 0.10011(2) = 1 * 2⁻¹ + 0 * 2⁻² + 0 * 2⁻³ + 1 * 2⁻⁴ + 1 * 2⁻⁵ = 1 * 0.5 + 1 * 0.0625 + 1 * 0. 03125 = 0.59375(10)
-
이진수 1100101.10011을 8진수와 16진수로 각각 올바르게 변환한 것은?
a. 145.46 65.98
- 2진수를 8진수 또는 16진수로 변환하기 위해서는 2진수 표현에서 소수점을 기준으로 정수 부분에 대해서는 왼쪽 방향, 소수 부분에 대해서는 오른쪽 방향으로 세 자리씩 묶어서 나타내면 8진수의 한 자릿수가 되고, 네 자리씩 묶어서 나타내면 16진수의 한 자릿수가 됨
- 8진수로의 변환
- 1100101.10011 → 001 100 101 . 100 110 → 1 4 5 . 4 6 (8)
- 16진수로의 변환
- 1100101.10011 → 0110 0101 . 1001 1000 → 6 5 . 9 8 (16)
-
2의 보수 방식을 사용해서 8비트로 표현된 정수 10100001은 10진수로 얼마인가?
a. -95
- 주어진 음수를 2의 보수 방식으로 표현하기 위해서는
- 주어진 음수의 절대 값을 이 진수로 변환
- 이진수의 각 비트에 대해서 보수(0은 1로, 1은 0으로 바꿈)를 취함
- 그 결과에 1을 더하면 됨
- 하지만 주어진 문제는 반대의 경우이기 때문에 위의 과정(주어진 음의 정수를 2의 보수 방법으로 변환하는 과정)의 역 순으로 처리하면 됨
- 즉 2의 보수로 표현된 수에서 1을 빼고(10100001 - 1 = 10100000), 그 결과에 대해서 보수를 취하면 01011111이 되고, 이것을 십진수로 변환하면 95가 되는데, 2의 보수 방식으로 표현된 수의 부호 비트가 1이므로 음의 정수 -95가 됨
- 주어진 음수를 2의 보수 방식으로 표현하기 위해서는
-
십진수 53.625를 부동 소수점 방식의 실수 표현으로 올바르게 것은? (단, 주어진 부동소수점은 16비트를 사용한다. 이 중에서 지수를 위해 5비트를 할당하며 초과_15 표기법을 사용한다.)
a. 0 10100 1010110100
- 주어진 실수를 이 진수로 변환(정수 부분과 소수 부분으로 구분하여 처리)하면 110101.101가 되고, 이에 대해 정규화를 수행하면 1.10101101 * 2⁵가 됨
- 부호 비트(1비트) → 주어진 수가 0보다 크므로 0이 됨
- 지수 → 지수 값 5와 매직 넘버 15를 더한 값 20을 이진수로 변환해서 5비트에 할당하면 10100이 됨
- 가수 → 소수점의 왼쪽 1을 제외한 나머지 부분(10101101)을 10비트(16비트 중에서 부호 1비트와 지수 5비트를 사용하고 남은 비트)에 할당하면 1010110100이 됨
-
다음 설명에 해당하는 문자 코드 체계는 무엇인가?
1 2
1995년 국제 표준으로 제정되었으며, 공식 명칭은 ISO/IEC 10646- 1이다. 16비트 코드 체계로서, 세계의 모든 문자를 표현할 수 있다.
a. 유니코드
- 유니코드는 애플 컴퓨터, IBM, MS 등의 컨소시엄을 통해 세계의 모든 문자를 컴퓨터에서 일관되게 표현하고 다룰 수 있도록 설계된 산업 표준으로, 사용 중인 플랫폼, 프로그램 등에 무관한 특징을 갖음
정리 하기
- 데이터와 정보
- I = P(D)
- 데이터와 정보의 관계
- 데이터 D를 대상으로 처리기 P에서 처리해서 얻은 결과가 정보 I임
- 데이터
- 현실 세계로부터 관찰이나 측정을 통해 단순히 얻어지는 사실이나 값
- 정보
- 어떤 상황에 대해 적절한 의사 결정을 수행할 수 있게 하는 지식
- 데이터 처리(정보 처리)
- 데이터를 정보로 가공하고 변환하는 일련의 과정
- 모든 데이터는 유형에 무관하게 비트 패턴이라는 일관된 방식으로 표현
- 데이터의 표현 단위
- bit, byte, KB, MB, GB, TB, PB, EB, ZB, YB
- 워드(word)
- 컴퓨터 연산의 기본 단위가 되는 정보의 양
- I = P(D)
- 진법
- r진법
- 0, 1, …, (r - 1)까지의 숫자만을 사용해서 수를 표현하는 방식/단위
- 2 진법, 8 진법, 10 진법, 16 진법 간의 변환이 필요
- 2진수/8진수/16진수를 10진수로 변환
- 각 위치에서의 숫자 값과 해당 위치에서의 가중치(자릿 값)를 곱한 후, 그 결과들을 모두 더함
- 10진수를 r진수로 변환
- 정수 부분과 소수 부분을 나눠서 각각 변환한 후, 그 결과를 단순히 연결해서 표현함
- 정수 부분에 대해서는 나눗셈을 적용한 후 나머지를 결과로 활용, 소수 부분에 대해서는 곱셈을 적용한 후 정수 부분을 결과로 활용
- 2진수와 8진수/16진수의 관계
- 2진수의 3 자릿수 = 8진수의 1 자릿수
- 2진수의 4 자릿수 = 16진수의 1 자릿수
- 2진수/8진수/16진수를 10진수로 변환
- r진법
- 정수 표현
- 정수 표현 방법의 종류
- 부호 없는 정수
- 부호 있는 정수
- 부호화-크기 방식
- 1의 보수 방식
- 2의 보수 방식
- 부호 없는 정수
- 부호 비트가 없으며, 주어진 n비트 전체를 사용해서 정수(0 ~ 2ⁿ - 1)를 표현
- 부호 있는 정수
- 부호화-크기 방식
- 최상위 1 비트를 부호 비트로 사용하고, 음의 정수는 음수에 대한 절대 값으로 표현
- 1의 보수 방식
- 부호 비트 사용
- 음의 정수는 양의 정수 표현에 대해 보수(0 → 1, 1 → 0)를 취해서 표혐
- 2의 보수 방식
- 부호 비트 사용
- 음의 정수는 1의 보수 방식의 결과에 1을 더해서 표현
- 부호화-크기 방식
- 정수 표현 방법의 종류
- 실수 표현
- 부동 소수점 방식을 사용해서 표현
- 표현 형식
- (-1)부호 × 가수 × 2지수
- (-1)ˢ × M × 2ᵉ
- 부호(1비트) + 지수(m비트) + 가수(n비트)
- 지수의 표현
- 초과 표기법
- 부동 소수점의 지수 부분만을 위한 표기 방법
- 지수를 m비트로 표현하는 경우 두 개의 매직 넘버(2ᵐ⁻¹, 2ᵐ⁻¹ - 1) 중에서 하나를 사용
- 부동 소수점의 지수 부분만을 위한 표기 방법
- 지수 값을 저장하는 경우
- (지수 값 + 매직 넘버)를 2진수로 표현/저장
- 저장 된 지수 값을 해석하는 경우
- (지수 부분의 2진수 값 - 매직 넘버)
- 초과 표기법
- 가수의 표현
- 정규화
- 소수점 바로 왼쪽에 오직 하나의 1만 있도록 소수점의 위치를 조정
- 가수 값을 저장하는 경우에는 소수점 이하 부분만 저장
- 정규화
- 문자 표현
- 키보드로 입력 되는 문자를 내부적으로 2진수로 변환하여 처리하기 위해서는 문자마다 유일한 코드를 부여할 수 있는 약속 된 문자 체계가 필요
- 대표적인 문자 체계의 종류
- ASCII (또는 확장된 ASCII)
- 유니코드