학습 개요
- 컴퓨터 프로그래밍을 시작하면서 가장 기본이 되는 내용인 자료 구조를 살펴봄
- 비선형 자료 구조인 트리와 그래프에 대해 알아보고, 그래프와 트리의 순회 방법과 표현 방법에 대해서 학습함
- 트리는 계층 구조를 표현하기에 적당하고, 그래프는 현실 세계 네트워크나 네비게이션의 목적지와 출발지를 표현하고 계산하는 데 가장 많이 사용되는 자료구조임
학습 목표
- 트리와 그래프와 같은 자료 구조에 대해서 이해할 수 있음
- 트리의 노드를 순회할 수 있는 방법에 대해서 이해할 수 있음
- 그래프의 노드를 순회하는 방법에 대해서 이해할 수 있음
강의록
트리
트리 용어 정의
- 개념
데이터 간의 관계를 나타내는 비선형 자료 구조
![image]()
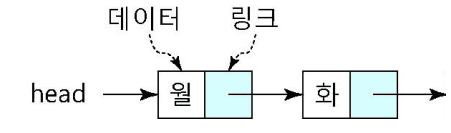
- 노드(node)라고 불리는 부분과 노드를 연결하는 가지(branch, edge)로 구분됨
노드 사이에는 계층적인 관계성을 갖음
![image]()
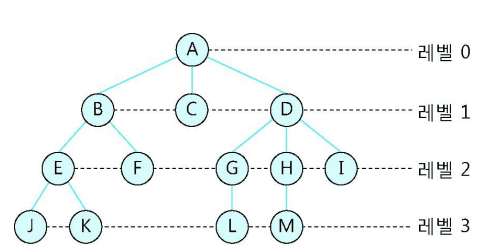
- 노드(node)
- 정보 항목을 의미함
- 루트(root)
- 빈 트리가 아닌 경우에 맨 꼭대기에 있는 하나의 노드
- 차수(degree)
- 각 노드에 있는 가지의 수
- 잎 노드(leaf node) = 단말 노드(terminal node)
- 노드의 차수가 0인 노드
- 내부 노드(internal node) = 비단말 노드(non-terminal node)
- 루트 노드와 단말 노드를 제외한 나머지 노드
- 조상(선조) 노드
- 루트 노드로부터 어떤 노드 X까지의 경로(가지들의 모음) 상에 존재하는 모든 노드를 X의 조상 노드라고 함
- 자손(후손) 노드
- 어떤 노드 X에서 단말 노드까지의 경로 상에 존재하는 모든 노드를 자손 노드라고 함
- 레벨(level)
- 루트 노드로부터의 거리(가지의 수)를 의미함
![image]()
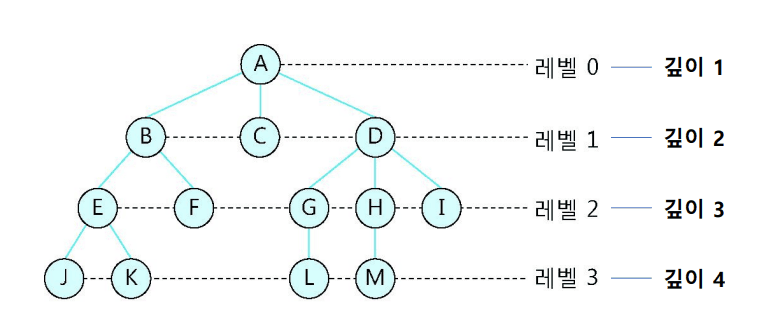
- 트리의 깊이(depth)/높이(height)
- 루트 노드로부터 가장 긴 경로에 있는 단말 노드의 레벨에 1의 값을 더한 것
- ex) 깊이 = 4
- 서브 트리(subtree)
- 특정 노드를 루트 노드로 하고, 그 아래에 있는 연결된 구조의 트리
- 숲(forest)
- n개의 서브 트리를 가진 트리에서 루트 노드를 제거해서 얻을 수 있는 분리 된 서브 트리의 집합
이진 트리
이진 트리(binary tree)
- 개념
- 트리 중에서 차수가 2인 트리
- 모든 노드의 차수는 최대 2를 넘지 않음
- 모든 노드는 최대 2개의 서브 트리를 가짐
![image]()
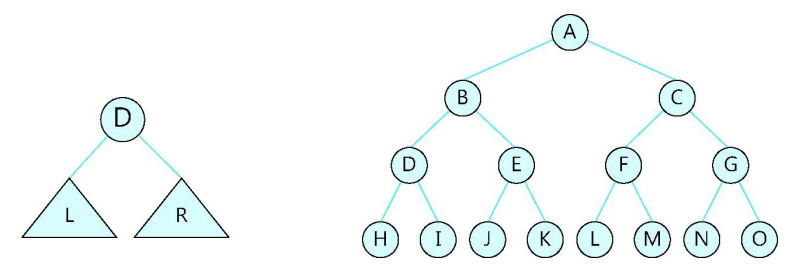
- 각 서브 트리는 왼쪽 서브 트리와 오른쪽 서브 트리로 구분 됨
- 왼쪽 노드와 오른쪽 노드에 순서의 의미를 부여함
- 이진 트리의 각 서브 트리는 다시 이진 트리가 됨
이진 트리의 높이
- 최대 높이
- N개의 노드를 가진 이진 트리의 높이를 계산으로 구할 수 있음
- 최대 높이
- N으로 노드의 개수와 같음
![image]()
- 최소 높이
모든 내부 노드가 최대 2개의 자식 노드를 갖는 경우로서 [log₂N ]+1이 높이가 됨
![image]()
이진 트리 순회 연산
- 개념
- 일정한 순서에 따라 트리에 있는 각 노드를 한 번씩 방문하는 것
![image]()
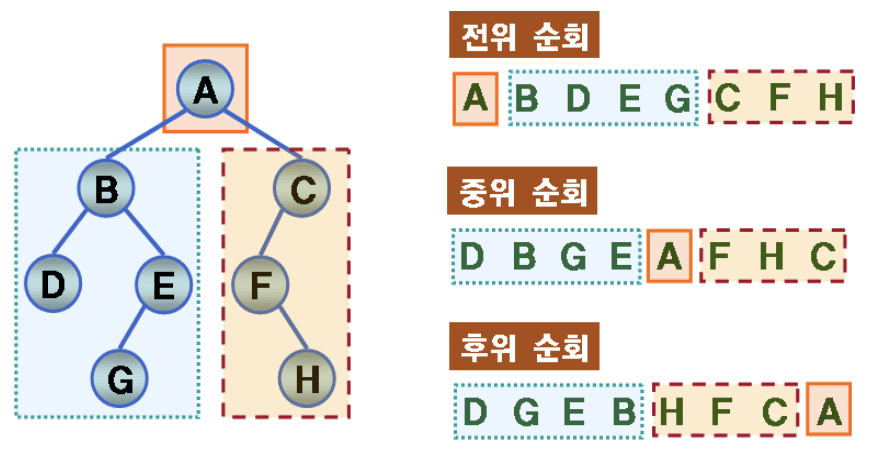
- DLR(전위 순회;preorder)
- 루트 노드 방문 → 왼쪽 서브 트리 방문 → 오른쪽 서브 트리 방문
- LDR(중위 순회;inorder)
- 왼쪽 서브 트리 방문 → 루트 노드 방문 → 오른쪽 서브 트리 방문
- LRD(후위 순회;postorder)
- 왼쪽 서브 트리 방문 → 오른쪽 서브 트리 방문 → 루트 노드 방문
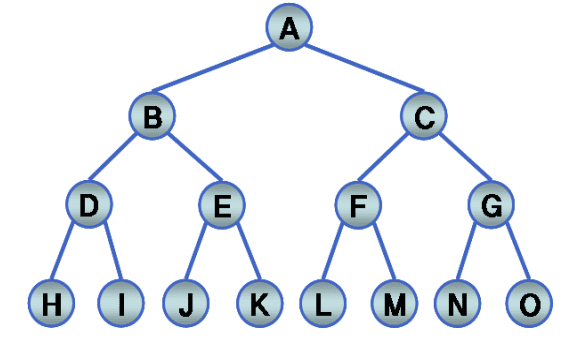
포화 이진 트리(full binary tree)
- 개념
- 깊이가 k인 이진 트리 중에서 노드의 개수가 2ᵏ - 1개인 이진 트리
- 깊이가 k인 이진 트리가 가질 수 있는 노드의 최대 개수는 2ᵏ - 1개
- 단말 노드의 개수가 2ᵏ - 1개
- 각 레벨에서 빈 자리가 없이 노드를 모두 가지고 있음
- 모든 내부 노드들은 2개의 자식 노드를 가짐
![image]()
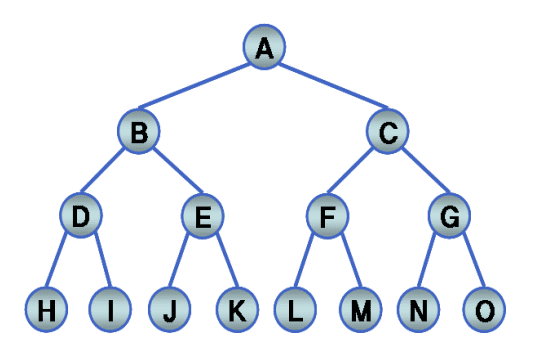
포화 이진 트리에서 각 노드에 번호를 부여한 경우
![image]()
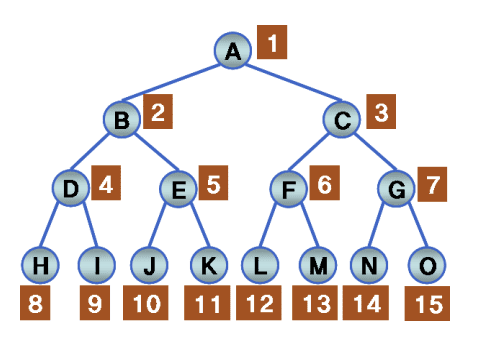
완전 이진 트리(complete binary tree)
- 개념
- 트리의 최대 레벨이 k일 때, 레벨 k-1까지는 포화 이진 트리를 형성하고, 레벨 k에서는 왼쪽부터 오른쪽으로 채워진 트리임
- 총 노드의 개수가 2ᵏ ⁺ ¹ - 1을 초과하지 않으면서, 포화 이진 트리의 노드 번호에 해당하는 연속적인 번호를 갖는 트리임
![image]()
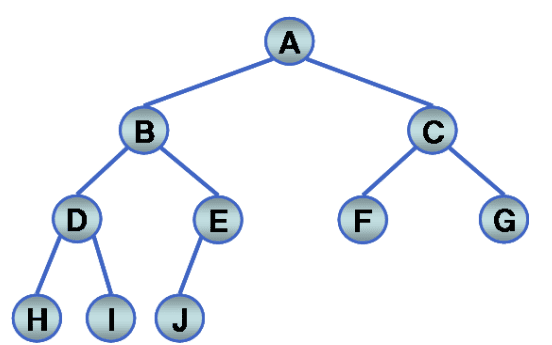
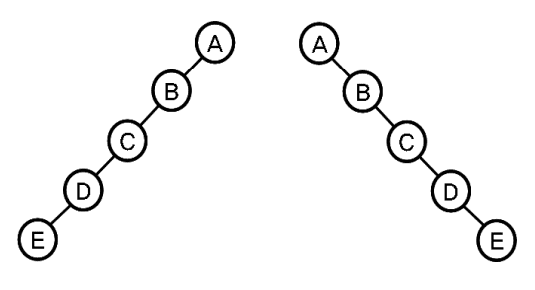
경사 이진 트리(skewed binary tree)
- 개념
- 한 쪽 방향으로만 가지가 뻗어 나간 이진 트리
- 왼쪽 방향으로만 가지가 뻗어 나간 경사 이진 트리
- 오른쪽으로만 가지가 뻗어 나간 경사 이진 트리
![image]()
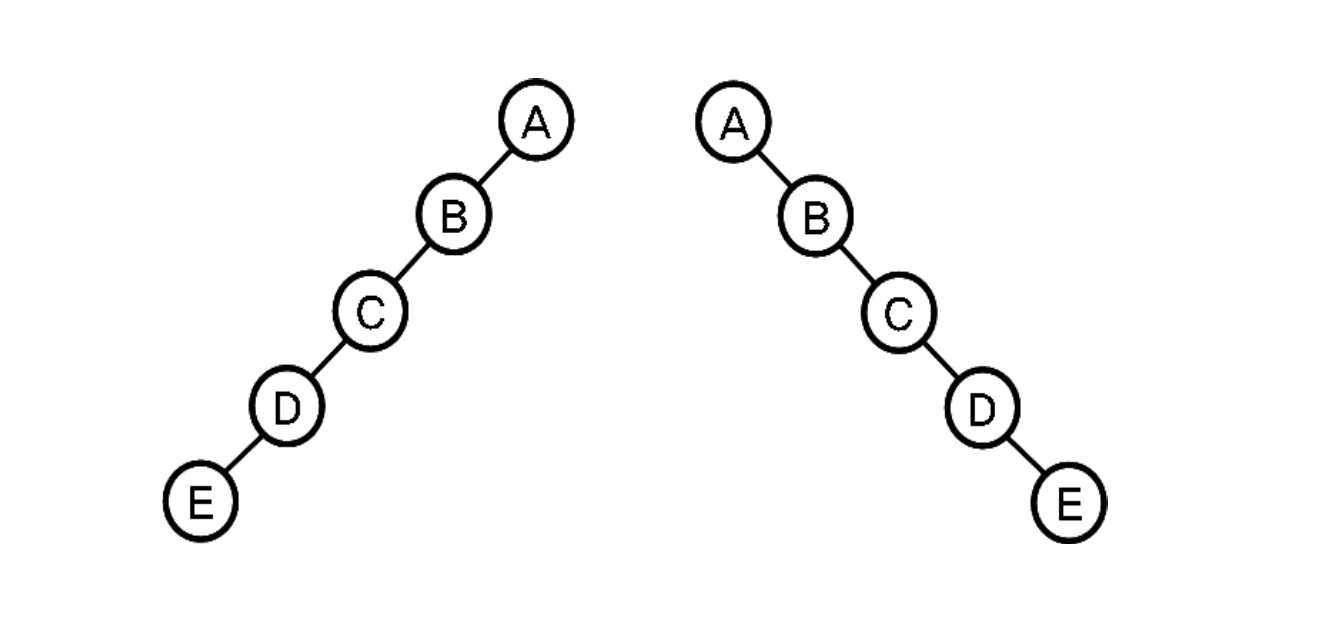
그래프
그래프의 개념과 용어
- 그래프 G
- 정점(vertext)들의 유한 집합 V와 두 개의 정점을 연결하는 간선(edge)들의 유한 집합 E로 정의
- G = (V, E)로 표시 됨
![image]()
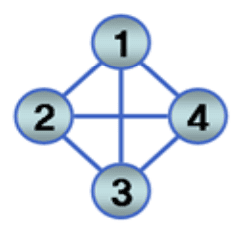
- 무방향 그래프(undirected graph)
- 간선이 방향성이 없는 간선으로 연결 된 그래프
![image]()
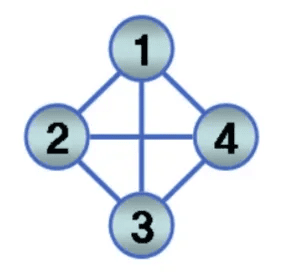
- 방향 그래프(directed digraph)
- 두 정점을 연결하는 간선이 방향성을 가지는 간선으로 연결 된 그래프
![image]()
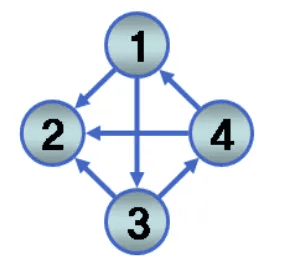
그래프의 집합 표현 방법
![image]()
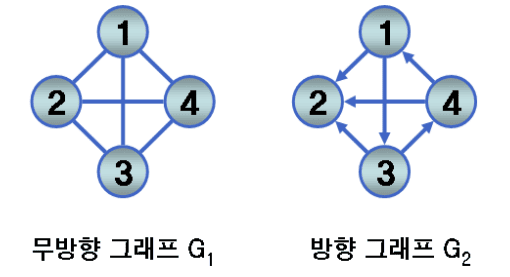
- G1 그래프
- V(G1) = {1, 2, 3, 4}
- E(G1) = {(1, 2),(1, 3),(1, 4),(2, 3),(2, 4),(3, 4)}
- G2 그래프
- V(G2) = {1, 2, 3, 4}
- E(G2) = {<1, 2>, <1, 3>, <3, 2>, <3, 4>, <4, 1>, <4, 2>}
- G1 그래프
- 용어
- 두 정점이 간선으로 직접 연결되어 있으면 두 정점은 인접(adjacent)해 있다고 하며 해당 간선은 두 정점에 부수(incident)되었다고 함
- 인접한다
- 정점 간의 관계
- 부수되었다
- 정점과 간선 간의 관계
- 경로 (path)
- 간선으로 연결된 정점들의 순차적 나열을 의미함
- 경로의 길이
- 경로에 포함된 간선의 개수
- 단순 경로 (simple path)
- 경로 상에 존재하는 정점들이 모두 다른 경로
- 사이클 (cycle)
- 세 개 이상의 정점을 가진 경로 중에서 시작 정점과 끝 정점이 같은 경로
- 단순 사이클 (simple cycle)
- 시작 정점과 끝 정점을 제외하고 모든 정점이 다른 사이클
- 두 정점은 서로 연결되었다
- 두 정점 사이에 경로가 존재함
- 그래프가 서로 연결되었다
- 무방향 그래프에서 서로 다른 모든 정점들 사이에 경로가 존재함
- 무방향 그래프에서 한 정점의 차수(degree)
- 정점에 부수된 간선의 개수임
- 방향 그래프 정점의 차수는 진입 차수와 진출 차수로 나뉨
- 진입 차수 (indegree)
- 다른 정점에서 해당 정점으로 향하는 간선의 개수
- 진출 차수 (outdegree)
- 해당 정점에서 다른 정점으로 향하는 간선의 개수
- 진입 차수 (indegree)
- 트리는 그래프의 특수한 형태로 봄
- 무방향 그래프에서 모든 정점이 서로 연결되어 있으면서 사이클이 존재하지 않는 그래프를 트리라고 함
그래프의 표현
그래프의 표현
- 개념
- 그래프를 컴퓨터 프로그래밍 언어로 구현하기 위해서는 인접 행렬(adjacency matrix)이나 인접 리스트(adjacency list)를 이용하여 표현함
- 인접 행렬을 이용하여 n개의 정점을 가진 그래프를 표현하기 위해서는 n×n 크기의 2차원 배열을 이용함
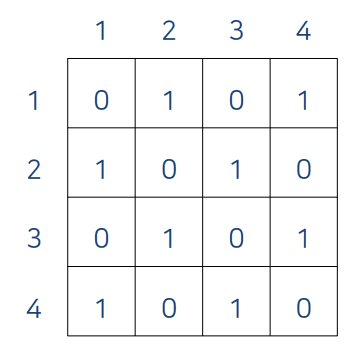
- 인접 행렬 A[i][j]에 값이 존재하면 그래프의 정점 vᵢ에서 정점 vⱼ 사이에 간선이 존재함을 의미하고 A[i][j]의 값은 1로 정함
- 인접 행렬
그래프
![image]()
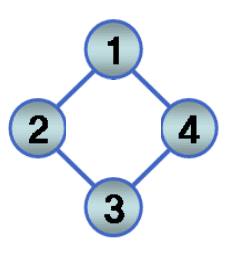
인접 행렬을 사용한 그래프의 표현
![image]()
- 인접 리스트
그래프
![image]()
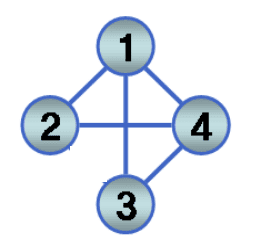
인접 리스트를 사용한 그래프의 표현
![image]()
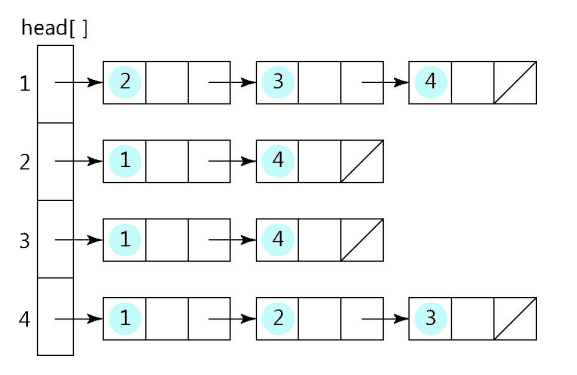
그래프의 탐색
- 개념
- 그래프의 모든 정점을 체계적으로 방문하는 것
깊이 우선 탐색 (depth first search)과 너비 우선 탐색 (breadth first search)이 있음
![image]()
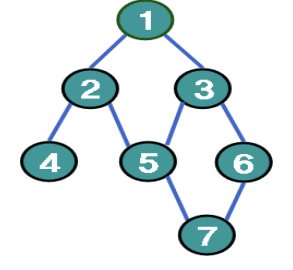
깊이 우선 탐색
- 개념
- 최근의 방문하지 않은 인접한 하나의 정점을 우선적으로 방문함
- 최종적인 방문 순서는 (1, 2, 4, 5, 7, 6, 3)이 됨
- 최종 방문 순서는 구현 방법에 따라 달라질 수 있음
너비 우선 탐색
- 개념
- 최근의 방문하지 않은 인접한 모든 정점을 모두 방문함
- 최종적인 방문 순서는 (1, 2, 3, 4, 5, 6, 7)이 됨
- 최종 방문 순서는 구현 방법에 따라 달라질 수 있음
정리 하기
- 트리
- 노드와 가지로 구성되어 나무 뿌리 모양의 데이터의 계층 관계를 나타내는 자료 구조
- 트리 순회 방법
- 전위 순회, 중위 순회, 후위 순회가 있음
- 그래프
- 정점들의 유한 집합과 정점들의 쌍을 연결하는 간선의 유한 집합
연습 문제
트리의 루트 노드에서 리프 노드에 이르는 가장 긴 경로에 존재하는 노드의 개수를 무엇이라고 하는가?
a. 깊이
- 노드를 연결하는 것을 가지(branch, edge)라고 하며, 각 노드에 있는 가지의 수를 차수(degree)라고 함
- 루트 노드로부터의 거리(가지의 개수)를 레벨이라고 함
- 레벨은 하나의 트리에서도 다를 수 있음
- 레벨에서 가장 큰 값을 트리의 깊이라고 함
이진 트리에 대한 설명으로 올바른 것은?
a. 노드가 하나도 없는 공백 트리도 이진트리임
- 이진 트리의 최대 차수는 2임
- 두 개까지의 자식 노드를 가질 수 있음
- 깊이가 2인 이진트리는 레벨 0에서 루트 노드 하나를 가지며, 레벨 1에서는 루트 노드의 자식 노드 2개를 가짐
- 레벨 2에서 4개의 노드를 가지기 때문에 최대 7개 노드 가질 수 있음
- 서브 트리는 대칭적인 관계를 가지는 것이 아님
그래프 관련 용어에 대한 설명으로 틀린 것은?
a. 각 정점과 인접해 있는 정점들의 나열을 사이클이라고 한다.
- 세 개 이상의 정점을 가진 경로 중에서 시작 정점과 끝 정점이 같은 경로를 사이클(cycle)이라고 함
- 그래프 관련 용어에 대한 설명
- 간선이 두 정점을 직접적으로 연결 시키고 있을 때 두 정점을 인접한 정점이라고 함
- 두 정점 사이에 경로가 존재하는 경우를 연결 되었다고 함
- 방향 그래프에서 적어도 두 정점이 연결되어 있지 않을 때 약하게 연결 되었다고 함
- 방향 그래프에서 적어도 두 정점 사이에 어느 한쪽으로만 경로가 존재할 때, 약하게 연결되었다고 함
정리 하기
- 트리
- 노드와 가지로 구성되어 나무 뿌리 모양의 데이터의 계층 관계를 나타내는 자료 구조
- 트리(tree)
- 데이터 간의 관계를 나타내는 비선형 자료구조로서 노드(node)라고 불리는 부분과 노드를 연결하는 가지(branch, edge)로 구분됨
- 잎 노드(leaf node)
- 단말 노드(terminal node)라고도 하며, 노드의 차수가 0인 노드
- 내부 노드(internal node)
- 비단말 노드(non-terminal node)라고도 하며, 루트 노드와 단말 노드를 제외한 나머지 노드
- 이진 트리 (binary tree)
- 트리 중에서 차수가 2인 트리를 의미하고, 모든 노드의 차수는 최대 2를 넘지 않으며 모든 노드는 최대 2개의 서브 트리를 가짐
- 이진 트리의 순회
- 일정한 순서에 따라 트리에 있는 각 노드를 한 번씩 방문하는 것
- 포화 이진 트리
- 이진 트리 중에서도 깊이가 k인 이진 트리가 가질 수 있는 최대 노드의 개수(-1)를 가진 이진 트리
- 완전 이진 트리
- 총 노드의 개수가 (-1)을 초과하지 않으면서 포화 이진 트리의 번호와 일치하는 이진 트리
- 경사 이진 트리
- 한쪽 방향으로 치우친 트리
- 트리 순회 방법으로 전위 순회, 중위 순회, 후위 순회가 있음
- 그래프 : 정점들의 유한 집합과 정점들의 쌍을 연결하는 간선의 유한집합
- 그래프(graph)
- 정점(vertex)들의 유한 집합 V와 두 개의 정점을 연결하는 간선(edge)들의 유한 집합 E로 정의되며, G=(V,E)로 표시됨
- 무방향 그래프(undirected graph)
- 간선이 방향성이 없는 간선으로 연결된 그래프
- 방향 그래프(directed graph, digraph)
- 두 정점을 연결하는 간선이 방향성을 가지는 간선으로 연결된 그래프
- 그래프의 표현
- 인접 행렬
- 인접 리스트
- 그래프 순회 방식
- 깊이 우선 탐색
- 너비 우선 탐색
- 그래프(graph)