💡해당 게시글은 방송통신대학교 이관용, 정광식 교수님의 '컴퓨터과학 개론' 강의를 개인 공부 목적으로 메모하였습니다.

학습 개요

알고리즘의 필요성과 정의에서부터 시작해서 알고리즘의 대표적인 설계 기법, 그리고 성능 분석 방법 등 알고리즘 전반에 걸친 주요 개념들에 대해서 살펴 봄
정렬 문제를 해결하는 가장 기본적인 형태의 알고리즘으로서 선택 정렬, 버블 정렬, 삽입 정렬에 대해서 학습함

학습 목표

알고리즘의 개념과 중요성을 이해할 수 있음
대표적인 알고리즘 설계 기법의 종류와 개념을 이해할 수 있음
알고리즘 분석을 위한 시간 복잡도와 점근 성능의 개념을 이해할 수 있음
선택 정렬, 버블 정렬, 삽입 정렬의 개념, 동작, 특징을 이해할 수 있음

강의록

알고리즘의 개념

문제를 해결하려면

컴퓨터 과학
- 컴퓨터를 활용해서 주어진 문제를 해결하는 학문
문제 풀이 방법/절차
- 알고리즘

알고리즘

문제 해결을 위한 레시피
- 단계적인 조리 절차(레시피)를 따르면 음식을 만들 수 있듯이, 주어진 문제도 단계적인 풀이 절차(알고리즘)를 따르면 문제의 해를 구할 수 있음
- 맛있고 좋은 음식 ↔ 효율적인 알고리즘

알고리즘의 정의

주어진 문제를 풀기 위한 명령어들을 단계적으로 나열한 것
- 주어진 문제에 대한 결과를 생성하기 위해 모호하지 않는 간단하고 컴퓨터가 수행 가능한 일련의 유한 개의 명령을 순서에 따라 구성한 것
- 입출력
  - 0개 이상의 외부 입력, 1개 이상의 출력 생성
- 명확성
  - 각 명령어는 모호하지 않고 단순 명확해야 함
- 유한성
  - 한정된 수의 단계를 거친 후에는 반드시 종료해야 함
- 유효성
  - 모든 명령어는 컴퓨터에서 실행할 수 있어야 함
- 실용적 측면
  - 효율적이어야 함

알고리즘 생성 단계

설계
표현/기술
정확성 검증
효율성 분석
- 방법
- 일상 언어
  - 단계 1. 계산할 n개의 숫자를 입력 받음
  - 단계 2. 입력 데이터를 모두 더해 합을 계산
  - 단계 3. 합을 출력
- 의사 코드
  1 2 3 4 5 sum = 0; while (데이터가 더 존재) sum = sum + 데이터(i); end print(sum);
- 순서도

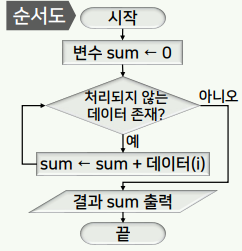
자료 구조와 알고리즘의 관계

자료 구조
- 데이터 사이의 논리적 관계를 표현하고 조직화하는 방법
- 기본적/대표적 종류
  - 배열, 연결 리스트, 스택, 큐, 트리, 그래프
효율적 프로그램 ← 자료구조 + 알고리즘
- 자료 구조에 대한 고려 없는 효율적인 알고리즘의 선택, 알고리즘에 대한 고려 없는 효율적인 자료 구조의 선택은 무의미

알고리즘의 설계

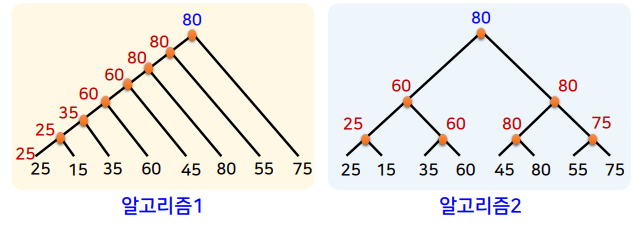
최댓값을 찾는 알고리즘

최댓값 찾기에서 알고리즘1과 알고리즘2 중에서 어떤 것이 더 효율적인가?

뒤섞인 카드 중에서 원하는 카드 찾기

주어진 카드를 섞어서 뒤집어 놓았다. 이 중에서 K를 찾아라!
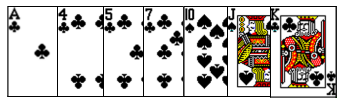
- 순차 탐색 (sequential search)

순서대로 나열된 카드 중에서 찾기

주어진 카드 중에서 10을 찾아라!
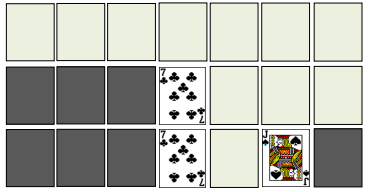
- 이진 탐색 (binary search)

알고리즘 설계에 적용할 방법?

주어진 문제와 그에 따른 조건 등이 매우 다양
- 일반적이고 범용적인 설계 기법은 없음
대표적인 설계 기법
- 분할 정복 divide-and-conquer 방법
- 동적 프로그래밍 dynamic programming 방법
  - 동적 계획법
- 욕심쟁이 greedy 방법
  - 탐욕적 방법

분할 정복 방법

순환적으로 recursively 문제를 푸는 방법
- 문제의 입력을 더 이상 나눌 수 없을 때까지 2개 이상의 작은 문제로 순환적으로 분할하고, 분할 된 문제들을 각각 해결한 후 이들의 해를 결합하여 원래 문제의 해를 구하는 하향식 접근 방법
특징
- 분할 된 작은 문제는 원래 문제와 동일, 단 입력 크기만 작아짐
- 분할 된 작은 문제는 서로 독립적
각 순환 호출 시 세 단계의 작업을 거침
- 분할
  - 주어진 문제를 여러 개의 작은 문제로 분할
- 정복
  - 작은 문제를 순환적으로 분할
  - 만약 작은 문제가 더 이상 분할 되지 않을 정도로 크기가 충분히 작다면 순환 호출 없이 작은 문제의 해를 구함
- 결합
  - 작은 문제에 대해 정복 된 해를 결합하여 원래 문제의 해를 구함
  - 결합 단계가 없는 문제도 존재
퀵 정렬, 합병 정렬, 이진 탐색

동적 프로그래밍 방법

최적화 문제의 해(최댓 값, 최솟 값)를 구하기 위한 상향식 접근 방법
- 문제의 크기가 작은 소 문제에 대한 해를 구해서 테이블에 저장해 놓고, 이를 이용하여 크기가 보다 큰 문제의 해를 점진적으로 만들어 가는 방법
  - 소 문제들이 서로 독립적일 필요 없음
플로이드 알고리즘
- 모든 정점 간의 최단 경로를 구하는 알고리즘

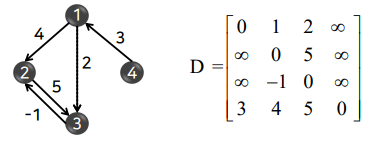
욕심쟁이 방법

해를 구하는 일련의 선택 과정마다 전후 단계의 선택과는 상관없이 각 단계에서 ‘가장 최선’이라고 여겨지는 국부적인 최적 해를 선택해 나가면 결과적으로 전체적인 최적 해를 얻을 수 있을 것이라고 희망하는 방법
- 희망
  - 각 단계의 최적 해를 통해 전체적인 최적 해를 만들어 내지 못할 수 있음
  - 적용 범위가 제한적, 간단하면서 강력한 설계 기법
- 거스름돈 문제, 배낭 문제

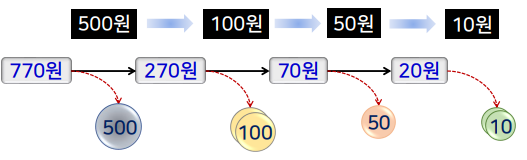
거스름돈 문제

고객에게 돌려줄 거스름돈이 T만큼 있을 때 고객이 받을 동전의 개수를 최소로 하면서 거스름돈을 돌려주는 방법을 찾는 문제
- 동전의 종류 → 500원, 100원, 50원, 10원

배낭 문제

최대 용량 M인 하나의 배낭, n개의 물체
- 각 물체 i에는 물체의 무게 wᵢ와 해당 물체를 배낭에 넣었을 때 얻을 수 있는 이익 pᵢ
배낭의 용량을 초과하지 않는 범위에서 배낭에 들어 있는 물체의 이익의 합이 최대가 되도록 배낭에 물체를 넣는 방법을 찾는 문제
- 가정
  - 물체를 쪼개서 넣을 수 있음
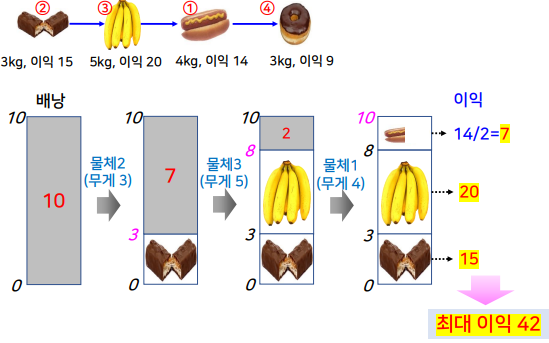
- 배낭 용량 10kg
  - M=10, n=4
  - (p1, p2, p3, p4)=(14, 15, 20, 9)
  - (w1,w2,w3,w4)=(4, 3, 5, 3)
- 단위 무게당 이익
  - (p1/w1, p2/w2, p3/w3, p4/w4)=(3.5, 5, 4, 3)
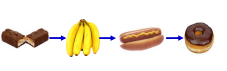
- 최대 이익 42

알고리즘의 분석

알고리즘 분석

정확성 분석
- 유효한 입력과 유한 시간 → 정확한 결과 생성?
  - 다양한 수학적 기법을 사용한 이론적 증명이 필요
효율성 분석
- 알고리즘 수행에 필요한 컴퓨터 자원의 양을 측정
- 공간 복잡도 (space complexity)
  - 메모리 양 = 정적 공간 + 동적 공간
- 시간 복잡도 (time complexity)
  - 수행 시간

시간 복잡도

알고리즘의 수행 시간
- 컴퓨터에서 실행시켜 완료될 때까지 걸리는 실제 시간을 측정하는 방법
  - 컴퓨터의 종류와 속도, 프로그래밍 언어, 프로그램 작성 방법, 컴파일러의 효율성 등에 종속적
    - 일반성 결여
- 알고리즘에서 수행되는 단위 연산의 수행 횟수를 모두 더한 값
  - 입력으로 제공되는 데이터의 크기(입력 크기)가 증가하면 수행 시간도 증가
    - 단순히 수행되는 단위 연산의 개수의 합이 아닌 입력 크기의 함수로 표현
  - 입력 데이터의 상태에 따라 달라짐
    - 평균 수행 시간, 최선 수행 시간, 최악 수행 시간
시간 복잡도

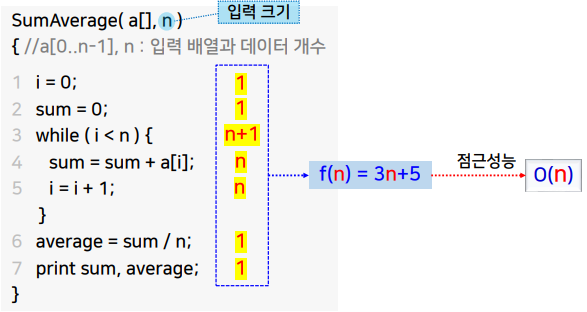
점근 성능

입력 크기 n이 충분히 커짐에 따라 결정되는 성능
다항식의 수행 시간에서 가장 큰 영향을 미치는 것은?
- 계수 없이 최고 차항만을 이용해 간략히 표현하는 성능
- 수행 시간의 어림 값, 수행 시간의 증가율이 주체
  - 알고리즘의 우열 비교가 용이

점근 성능의 표기법

Big-oh 점근적 상한
- 함수 f와 g를 각각 양의 정수를 갖는 함수라 하자.
- n ≥ n₀인 모든 n에 대하여 f(n) ≤ c ⋅ g(n)을 만족하는 양의 상수 c와 n₀이 존재하면 f(n) = O(g(n))이다.
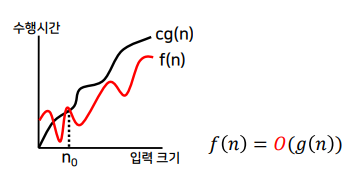
Big-omega 점근적 하한
- 함수 f와 g를 각각 양의 정수를 갖는 함수라 하자.
- n ≥ n₀인 모든 n에 대하여 f(n) ≥ c ⋅ g(n)을 만족하는 양의 상수 c와 n₀이 존재하면 f(n) = Ω(g(n))이다.
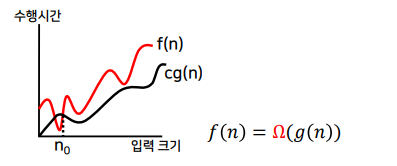
Big-theta 점근적 상하한
- 함수 f와 g를 각각 양의 정수를 갖는 함수라 하자.
- n ≥ n₀인 모든 n에 대하여 c₁ ⋅ g(n) ≤ f(n) ≤ c₂ ⋅ g(n)을 만족하는 양의 상수 c₁, c₂와 n₀이 존재하면 f(n)=Θ(g(n))이다.

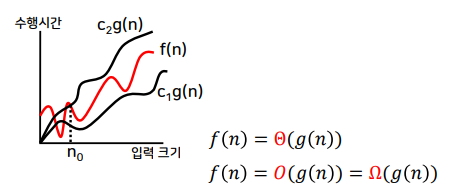
점근 성능의 표기법

f(n) = 3n + 3, g(n) = n
- n ≥ n₀에 대해서 f(n) ≤ c ⋅ g(n)을 만족 → n₀ = 2, c = 5 → f(n) = O(n)
- n ≥ n₀에 대해서 f(n) ≥ c ⋅ g(n)을 만족 → n₀ = 1, c = 3 → f(n) = Ω(n)
- f(n) = O(n) 이면서 f(n) = Ω(n) → f(n) = Θ(n)
f(n) = 2n³ + 3n² + 10 → O(n³)

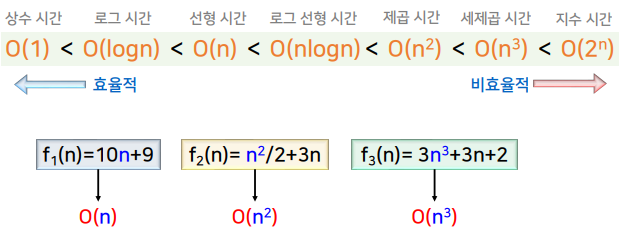
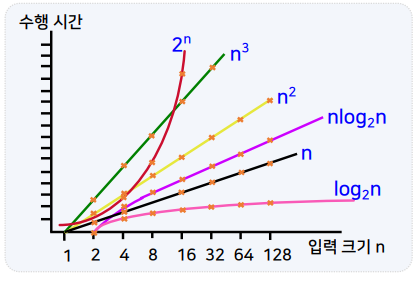
O - 표기 간의 연산 시간의 크기 관계

정렬 알고리즘: 선택 정렬, 버블 정렬, 삽입 정렬

기본 개념

정렬 (sort)
- 정렬 수행 시점에 데이터가 어디에 저장되어 있는가?
- 내부 (internal) 정렬
  - 모든 데이터를 주 기억 장치에 적재한 후 정렬하는 방식
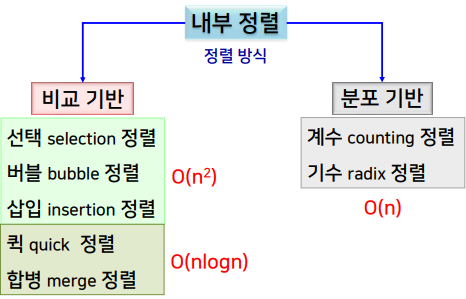
- 외부 (external) 정렬
  - 모든 데이터를 주 기억 장치에 저장할 수 없는 경우, 전체 데이터를 보조 기억 장치에 저장하고 그중의 일부 데이터를 번갈아 가면서 주 기억 장치로 적재해서 정렬하는 방식
정렬을 위한 기본 가정
- 키의 개수
  - n
- 키 저장
  - A[0..n−1]
- 키 값
  - 양의 정수
- 정렬 방식
  - 오름차순

선택 정렬

주어진 데이터 중에서 가장 작은 값부터 차례대로 선택해서 나열하는 방식
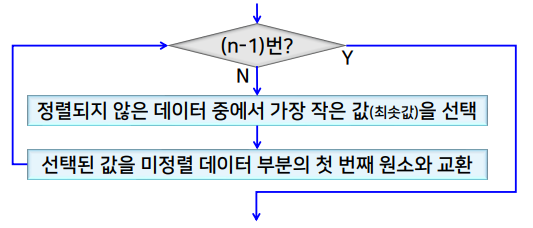
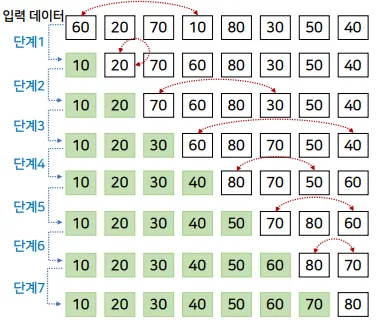
- 정렬되지 않은 데이터 중에서 가장 작은 값(최솟 값)을 선택
- 선택 된 값을 미정렬 데이터 부분의 첫 번째 원소와 교환
- O(n²)
  - 언제나 동일한 수행 시간
  - 데이터의 입력 상태에 민감하지 않은 수행 시간

버블 정렬

왼쪽에서부터 모든 인접한 두 데이터를 차례대로 비교하여 왼쪽의 값이 더 큰 경우에는 오른쪽 값과 자리를 바꾸는 과정을 반복

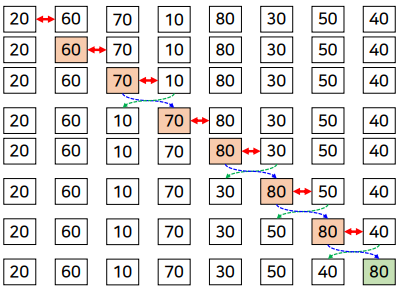
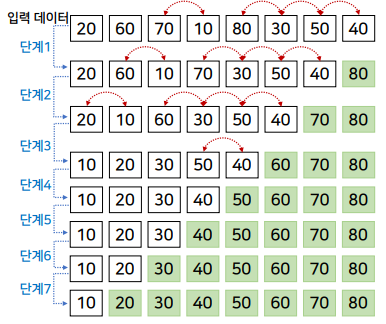
버블 정렬의 특징

성능
- 입력 데이터의 상태에 영향을 받음
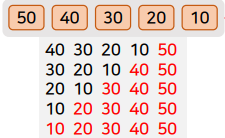
- 원하는 순서로 이미 정렬되어 있는 경우
  - 최선의 경우 O(n)
- 역 순으로 정렬되어 있는 경우
  - 최악의 경우 O(n2)
선택 정렬에 비해 데이터 교환이 더 많이 발생
- 선택 정렬보다 비효율적

삽입 정렬

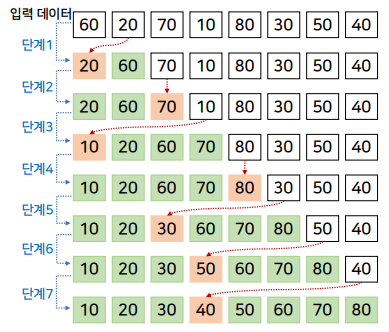
주어진 데이터를 하나씩 뽑은 후, 나열된 데이터들이 항상 정렬 된 형태를 가지도록 뽑은 데이터를 바른 위치에 삽입해서 나열하는 방식
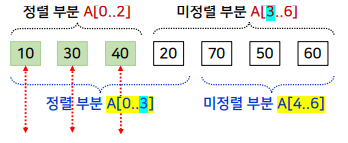
- 입력 배열을 정렬 부분과 미 정렬 부분으로 구분하고 미정렬 부분의 가장 왼쪽에 있는 데이터(“첫 번째 데이터”)를 뽑은 후, 정렬된 부분에서 제자리를 찾아서 삽입하는 과정을 반복
뽑은 데이터를 삽입할 제자리를 찾는 방법

삽입 정렬의 특징

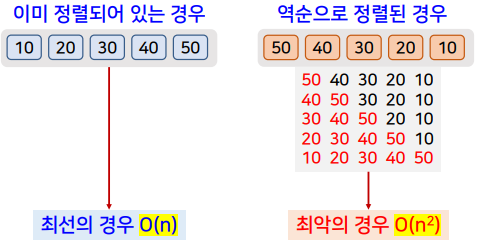
성능 → 입력 데이터의 상태에 영향을 받음

정리 하기

알고리즘의 개념
- 조건
  - 입출력, 명확성, 유한성, 유효성 + (효율성)
- 생성 단계
  - 설계 → 표현/기술 → 정확성 분석 → 효율성 분석
알고리즘의 설계
- 분할 정복 방법, 동적 프로그래밍 방법, 욕심쟁이 방법 (거스름돈 문제, 배낭 문제)
알고리즘의 분석
- 정확성 분석 + 효율성 분석 (공간 복잡도, 시간 복잡도)
- 시간 복잡도
  - 알고리즘의 수행 시간 (입력 크기의 함수, 최악 수행 시간)
- 점근 성능
  - 개념, 표기법 (O,Ω,Θ), O-표기의 크기 관계
정렬 알고리즘: 선택 정렬, 버블 정렬, 삽입 정렬
- 내부 정렬, 비교 기반
- 선택 정렬
  - O(n²)
  - 언제나 동일한 수행 시간
- 버블 정렬, 삽입 정렬
  - O(n²)
  - 입력 데이터의 상태에 민감
    - 최악 O(n²)
    - 최선 O(n)

연습 문제

문제 해결의 가능성이라는 이론적인 관점에서 알고리즘이 만족해야 할 조건에 해당하지 않는 것은?
a. 확장성
- 문제 해결 가능성이라는 이론적인 측면에서 알고리즘은 4가지의 조건(입출력, 명확성, 유한성, 유효성)을 모두 만족해야 함
  - 유효성
    - 모든 명령은 컴퓨터에서 실행 가능해야 함
  - 명확성
    - 각 명령은 모호하지 않고 단순 명확해야 함
  - 유한성
    - 한정 된 수의 단계를 거친 후에는 반드시 종료함
  - 입출력
    - 0개 이상의 외부 입력과 하나 이상의 출력이 있어야 함
- 알고리즘의 실용적인 관점에서는 알고리즘의 효율성도 중요한 조건이 됨
알고리즘의 대표적인 설계 기법으로서 거리가 먼 것은? a. 회귀 분석 방법
- 주어진 문제와 조건 등이 매우 다양하므로 범용적인 알고리즘의 설계 방법론은 존재하지 않지만 많은 부류의 문제에 적용될 수 있는 대표적인 설계 기법으로는 욕심쟁이 방법, 분할 정복 방법, 동적 프로그래밍 방법이 있음
- 알고리즘의 대표적인 설계 기법
  - 동적 프로그래밍 기법
  - 분할 정복 기법
  - 욕심쟁이 기법
다음과 같은 조건의 배낭 문제를 욕심쟁이 방법으로 해결할 때 가장 먼저 배낭에 넣는 물체는?(단, 물체는 쪼개서 배낭에 넣을 수 있다.)
1 2 3 4 5 배낭의 무게: 10kg 물체1 → 무게 5kg, 이익 20 물체2 → 무게 3kg, 이익 15 물체3 → 무게 4kg, 이익 14 물체4 → 무게 3kg, 이익 9
a. 물체 2
- 배낭의 용량을 초과하지 않는 범위 내에서 최대 이익을 얻기 위해서는 무게는 적으면서 이익이 큰 물체부터 최대한 배낭에 넣으면 됨
- 각 물체의 단위 무게 당 이익, 즉 각 물체의 이익을 무게로 나눈 값을 계산하여, 이 값이 큰 순서대로 배낭에 해당 물체를 최대한 넣음
알고리즘의 시간 복잡도에 대한 설명으로 올바른 것은? a. 입력 데이터의 상태에 따라 달라진다.
- 알고리즘의 시간 복잡도
  - 알고리즘에서 수행 되는 기본적인 연산들의 수행 횟수의 합으로 정의함
  - 단순히 단위 연산의 개수가 아닌 입력 크기 n의 함수로 표현함
  - 입력 되는 데이터의 상태에 따라 달라지므로, 일반적으로 최악의 수행 시간을 평가 척도로 사용함
f(n)=3n³+3n-1이라고 하고 g(n)=n³이라고 하자. n>1에 대하여 f(n)≤7g(n)일 때 f(n)에 대한 올바른 점근 성능의 표기는? a. f(n)=O(n³)
- 1보다 큰 모든 입력 크기 n에 대해서 알고리즘 수행 시간 f(n)이 7 · g(n)보다 작거나 같다는 것은 결국 알고리즘의 수행 시간 f(n)이 아무리 오래 걸려도 7 · g(n)보다 더 커질 수 없다는 점근적 상한을 의미하고, 점근적 상한에 해당하는 표기법은 Big-Oh임
- Big-Omega 표기법(Ω)은 점근적 하한(f(n) ≥ c · g(n))을 의미함
- Big-theta 표기법(Θ)은 점근적 상하한(c₁ · g(n) ≤ f(n) ≤ c₂ · g(n))을 의미함
미정렬 데이터 중에서 가장 작은 키 값을 갖는 데이터를 선택하고, 선택된 값과 미정렬 데이터 부분의 첫 번째 데이터와 교환하는 방식의 정렬 알고리즘은?(단, 오름차순으로 정렬한다.)
a. 선택 정렬
- 선택 정렬은 주어진 데이터 중에서 가장 작은 값부터 차례대로 선택해서 나열하는 방식임
버블 정렬에 대한 설명으로 올바른 것은?
a. 선택 정렬에 비해 데이터 교환이 많이 발생한다.
- 선택 정렬에 비해 데이터 교환이 많이 발생하기 때문에 버블 정렬은 선택 정렬보다 비효율적임
- 버블 정렬
  - 입력 데이터가 역순으로 정렬 된 경우에는 최악의 성능 O(n²)를 가짐
  - 선택 정렬에 비해 데이터 교환이 많이 발생함
- 선택 정렬
  - 데이터의 입력 상태에 민감하지 않은 수행 시간을 갖음
- 삽입 정렬
  - 정렬되지 않는 부분의 첫 번째 데이터를 선택해서 정렬된 부분에 위치 시킴

정리 하기

기본 개념
- 컴퓨터 알고리즘이란?
  - 주어진 문제에 대한 하나 이상의 결과를 생성하기 위해 모호하지 않고 간단하며 컴퓨터가 수행 가능한 일련의 유한 개의 명령들을 순서적으로 구성한 것
- 이론적 관점에서 반드시 만족해야 할 조건
  - 입출력, 명확성, 유한성, 유효성
- 실용적 관점에서의 추가 조건
  - 효율성
알고리즘 설계
- 대표적인 설계 기법
  - 분할 정복 방법, 동적 프로그래밍 방법, 욕심쟁이 방법
  - 분할 정복법
    - 순환적으로 문제를 푸는 방식
    - 문제를 더 이상 나눌 수 없을 때까지 두 개 이상의 작은 문제로 순환적으로 분할하고, 분할된 문제들을 각각 해결한 후 이들의 해를 결합하여 원래 문제의 해를 구하는 하향식 접근 방법으로, 각 순환 호출 시마다 분할, 정복, 결합의 세 단계를 거침
    - 적용 가능한 문제
      - 퀵 정렬
      - 합병 정렬
      - 이진 탐색
  - 동적 프로그래밍 방법
    - 문제의 크기가 가장 작은 소 문제부터 해를 구해서 테이블에 저장해 놓고 이를 이용하여 입력 크기가 보다 큰 원래의 문제를 점진적으로 만들어가는 상향식 접근 방법
    - 적용 가능한 문제
      - 모든 정점 간의 최단 경로를 구하는 플로이드 알고리즘
  - 욕심쟁이 방법
    - 해를 구하는 일련의 선택 과정마다 전후 단계의 선택과는 상관없이 각 단계에서 ‘가장 최선’이라고 여겨지는 국부적인 최적 해를 선택해 나가면 결과적으로 전체적인 최적 해를 얻을 수 있을 것이라고 희망하는 방법
    - 거스름돈 문제
      - 고객에서 돌려줄 거스름돈이 T만큼 있을 때 고객이 받을 동전의 개수를 최소로 하면서 거스름돈을 돌려주는 방법을 찾는 문제
        단순히 동전의 액면가가 가장 큰 동전부터 차례대로 최대한 거스름돈을 만듬
    - 배낭 문제(물체를 쪼갤 수 있는 경우)
      - 배낭의 용량을 초과하지 않는 범위에서 배낭에 들어 있는 물체의 이익의 합이 최대가 되도록 배낭에 물체를 넣는 방법을 찾는 문제
        단위 무게 이익이 가장 큰 물체부터 통째로 배낭에 넣고, 만약에 배낭의 남은 용량보다 물체의 무게가 큰 경우에는 물체를 쪼개서 배낭에 넣는다.
알고리즘 분석
- 정확성 분석
  - 유효한 입력이 주어졌을 때 유한 시간 내에 정확한 결과를 생성하는 지를 수학적으로 증명
- 효율성 분석
  - 알고리즘 수행에 필요한 컴퓨터 자원, 즉 소요되는 메모리 공간의 크기
  - (공간 복잡도)와 수행에 걸리는 시간(시간 복잡도)을 측정
- 시간 복잡도
  - 알고리즘의 수행 시간
    - 알고리즘에서 수행되는 기본적인 연산의 수행 횟수의 합
  - 단순히 단위 연산의 개수가 아닌 입력 크기의 함수로 표현
  - 입력 데이터의 상태에 따라 달라지며, 일반적으로 최악의 수행 시간을 사용
- 점근 성능
  - 입력 크기 n이 충분히 커질 때 알고리즘의 수행 시간이 무엇에 의해 좌우되는 가를 나타내는 성능
    - 수행 시간이 다항 식으로 표현되는 경우 입력 크기가 커짐에 따라 차수가 낮은 항들의 역할은 감소하고, 결국 계수 없이 n의 최고 차항만을 이용해서 표현
    - 수행 시간의 어림 값이지만 수행 시간의 증가 추세 파악이 용이하여 알고리즘의 우열을 따질 때 사용
  - 표기법
    1. Big-Oh 점근적 상한 f(n) = O(g(n))
    2. Big-Omega 점근적 하한 f(n) = Ω(g(n))
    3. Big-Theta 점근적 상 하한 f(n) = Θ(g(n))
  - 빅오 표기 간의 연산 시간의 크기 관계
    - O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(n³) < … < O(2ⁿ)
정렬 알고리즘
- 내부 정렬 vs 외부 정렬
  - 내부 정렬
    - 모든 데이터를 주 기억 장치에 적재한 후 정렬하는 방식
  - 외부 정렬
    - 모든 데이터를 주 기억 장치에 저장할 수 없는 경우, 일부 데이터만 주 기억 장치에 있고 나머지는 외부 기억 장치에 저장한 채 정렬하는 방식
- 비교 기반 정렬 vs 분포 기반 정렬
  - 비교 기반 정렬
    - 데이터의 키 값을 직접 비교하여 정렬하는 방식
    - 선택 정렬, 버블 정렬, 삽입 정렬, 퀵 정렬, 합병 정렬
  - 분포 기반 정렬
    - 데이터의 분포 정보를 사전에 얻어서 정렬에 이용하는 방법
    - 계수 정렬, 기수 정렬
- 선택 정렬
  - 주어진 데이터 중에서 가장 작은 값부터 차례대로 선택해서 나열하는 방식
    1. 미정렬 부분의 데이터 중에서 가장 작은 값을 선택하고
    2. 선택된 값과 미 정렬 부분의 첫 번째 데이터와 교환
  - 데이터의 입력 상태에 민감하지 않고 언제나 동일한 수행 시간
    - O(n²)
- 버블 정렬
  - 왼쪽에서부터 모든 인접한 두 데이터를 차례대로 비교하여 왼쪽의 값이 더 큰 경우에는 오른쪽 값과 자리 바꿈을 통해 정렬하는 방법
  - 데이터가 원하는 순서로 이미 정렬된 경우에는 O(n)을 갖고, 역 순으로 정렬된 경우에는 최악의 수행 시간 O(n²)을 가짐
  - 데이터의 교환이 많이 발생하여 선택 정렬보다 비효율적
- 삽입 정렬
  - 주어진 데이터를 하나씩 뽑은 후, 나열된 데이터들이 항상 정렬된 형태를 가지도록 뽑은 데이터를 바른 위치에 삽입해서 나열하는 방식
    - 미 정렬 부분의 첫 번째 데이터를 꺼낸 후, 정렬된 부분에서 제자리를 찾아 삽입하는 과정을 반복
  - 주어진 데이터가 이미 정렬된 경우에는 최선의 수행 시간 O(n)을 갖고, 데이터가 역 순으로 정렬된 경우에는 최악의 수행 시간 O(n²)을 가짐

[컴퓨터과학 개론] 5강 - 알고리즘

학습 개요

학습 목표

강의록

알고리즘의 개념

문제를 해결하려면

알고리즘

알고리즘의 정의

알고리즘 생성 단계

자료 구조와 알고리즘의 관계

알고리즘의 설계

최댓값을 찾는 알고리즘

뒤섞인 카드 중에서 원하는 카드 찾기

순서대로 나열된 카드 중에서 찾기

알고리즘 설계에 적용할 방법?

분할 정복 방법

동적 프로그래밍 방법

욕심쟁이 방법

거스름돈 문제

배낭 문제

알고리즘의 분석

알고리즘 분석

시간 복잡도

점근 성능

점근 성능의 표기법

점근 성능의 표기법

O - 표기 간의 연산 시간의 크기 관계

정렬 알고리즘: 선택 정렬, 버블 정렬, 삽입 정렬

기본 개념

선택 정렬

버블 정렬

버블 정렬의 특징

삽입 정렬

삽입 정렬의 특징

정리 하기

연습 문제

정리 하기

Further Reading

[컴퓨터과학 개론] 4강 - 자료 구조

[컴퓨터과학 개론] 1강 - 컴퓨터와 자료

[컴퓨터과학 개론] 2강 - 컴퓨터와 데이터