Home [데이터베이스 시스템] 11강 - 인덱싱
Post
Cancel

[데이터베이스 시스템] 11강 - 인덱싱

Posted May 6, 2025
By mxxikr
read 25 min

💡해당 게시글은 방송통신대학교 정재화 교수님의 '데이터베이스 시스템' 강의를 개인 공부 목적으로 메모하였습니다.



학습 개요

  • 현실의 데이터베이스 응용에서는 대부분의 질의가 전체 데이터가 아닌 일부의 레코드만을 대상으로 함
  • 별도의 검색 구조 없이 조건을 만족하는 레코드를 찾기 위해서는 파일 내의 모든 레코드를 처음부터 끝까지 순차적으로 확인해야 하며, 이러한 방식은 데이터 양이 많아질수록 성능 저하가 급격하게 발생하게 됨
  • 이를 해결하기 위해 DBMS는 인덱스라 불리는 자료 구조를 이용하여 특정 레코드를 보다 효율적으로 탐색할 수 있도록 지원함
  • 인덱스의 개념과 필요성, 그리고 인덱싱 기법의 기본적인 분류 방식에 대해 다루고 관계형 데이터베이스에서 가장 널리 사용되는 B+-트리 인덱스의 구조적 특징과 삽입, 삭제, 탐색 연산의 동작 방식을 중심으로 인덱스가 실제로 어떻게 구성되고 동작하는 지를 구체적으로 학습함



주요 용어

  • 탐색 키
    • 한 파일에서 레코드를 찾기 위해 사용되는 컬럼이나 컬럼 값의 집합
  • 인덱스 엔트리
    • 탐색 키와 탐색 키에 해당하는 레코드의 레코드 포인터의 쌍을 저장한 구조
  • 다단계 인덱스
    • 인덱스를 외부 인덱스와 내부 인덱스의 다단계 구조로 나누어 외부 인덱스에서 희소하게 분포 시켜 인덱스 파일의 크기를 적정하게 유지할 수 있는 인덱스
  • 이진 탐색 트리
    • 이진 트리의 일종으로 왼쪽은 부모 노드보다 작은 노드 값, 오른쪽에는 부모 노드보다 큰 노드 값을 위치 시켜 특정 노드 값을 빠르게 찾을 수 있도록 구조화한 트리



강의록

인덱스의 이해

일반적인 데이터 검색 과정

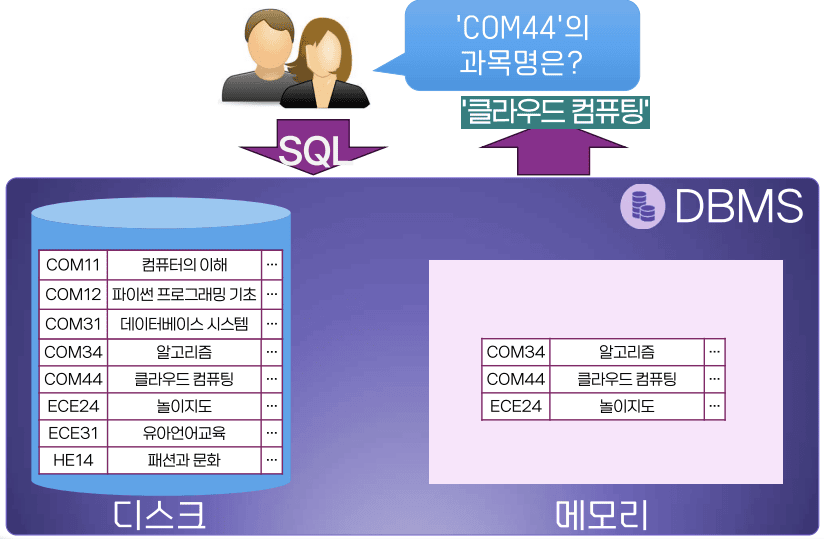
image.png

  • 레코드 3개가 하나의 블록 단위로 메모리 사이에 입출력 된다고 가정

인덱스의 개념

  • 데이터 검색 시 발생하는 비효율적인 데이터 입출력 문제를 해결하기 위한 목적으로 시작
    • 인덱스
      • 요청된 레코드에 빠르게 접근할 수 있도록 지원하는 데이터와 관련된 부가적인 구조
    • 인덱싱
      • 인덱스를 구성하고 생성하는 작업
  • 인덱스의 탐색 키를 이용하여 해당 레코드가 저장 된 블럭의 위치를 파악하고 해당 블럭을 빠르게 적재
  • 탐색 키(검색 키)
    • 파일에서 레코드를 찾는데 사용되는 컬럼이나 컬럼의 집합

인덱스 기반의 데이터 검색 과정

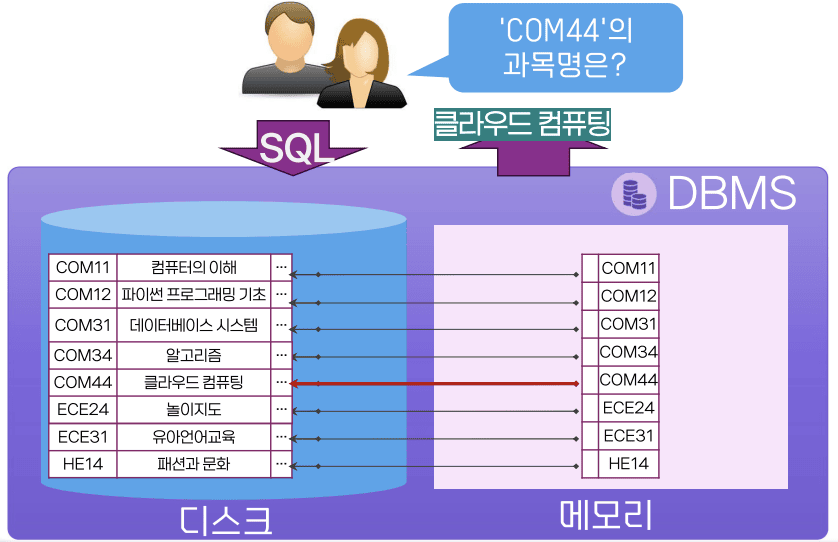
image.png

인덱스의 종류와 평가 기준

  • 인덱스의 종류
    • 순서 인덱스
      • 특정 값에 대해 정렬된 순서 구조
    • 해시 인덱스
      • 버킷의 범위 안에서 값의 균일한 분포에 기초한 구조로 해시 함수가 어떤 값이 어느 버킷에 할당되는지 결정
  • 인덱스의 평가 기준
    • 접근 시간
      • 데이터를 찾는 데 소요되는 시간
    • 유지 비용
      • 새로운 데이터 삽입 및 기존 데이터 삭제 연산으로 인한 인덱스 구조 갱신 비용
    • 공간 비용
      • 인덱스 구조에 의해 사용되는 부가적인 공간 비용

순서 인덱스

순서 인덱스의 특징

  • 탐색 키로 정렬된 순차 파일에 대하여 레코드에 대한 빠른 접근이 가능하도록 구성한 인덱스
    • 탐색 키를 정렬하여 해당 탐색 키와 탐색 키에 대한 레코드와의 연계를 통하여 인덱스 생성
  • 순서 인덱스의 종류
    • 밀집 인덱스
    • 희소 인덱스
    • 다단계 인덱스

순차 파일 구조

  • 다음 레코드 위치를 알려주는 포인터

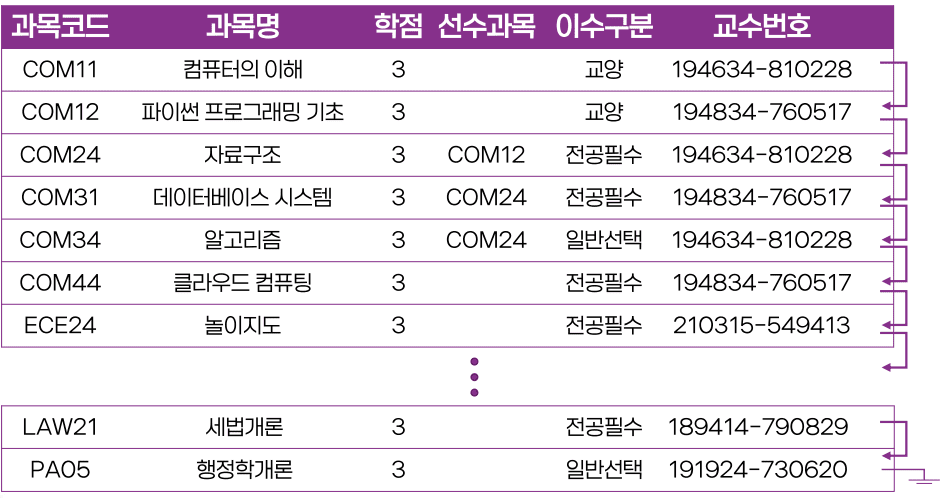
    image.png

    • 범위 검색에는 유리하나 첫 요청 레코드 찾기는 어려움

인덱스 엔트리

  • 인덱스 엔트리 구조

    image.png

    • 블럭 ID
      • 해당 레코드는 어느 블록에?
    • 오프셋
      • 해당 블록의 몇 번째에 위치?

  • 인덱스 엔트리 구성

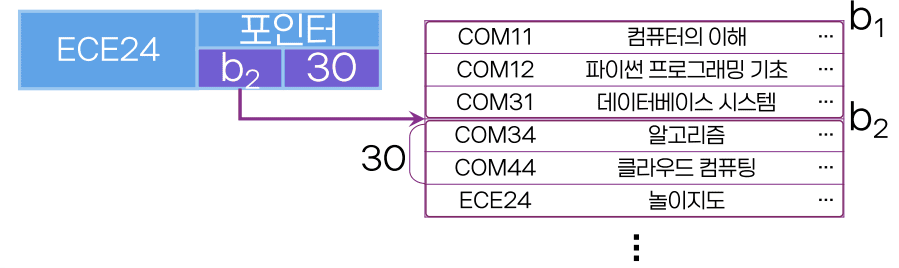
    image.png

    • 인덱스 엔트리가 담아내야 하는 것들
      1. 어떤 정보를 담고 있는지?
      2. 디스크 어느 위치에 저장?

밀집 인덱스(dense index)

  • 모든 레코드에 대해 탐색 키 값:포인터 쌍을 유지
    • 모든 인덱스에 대해 인덱스 엔트리를 유지해서 사용하는 인덱스

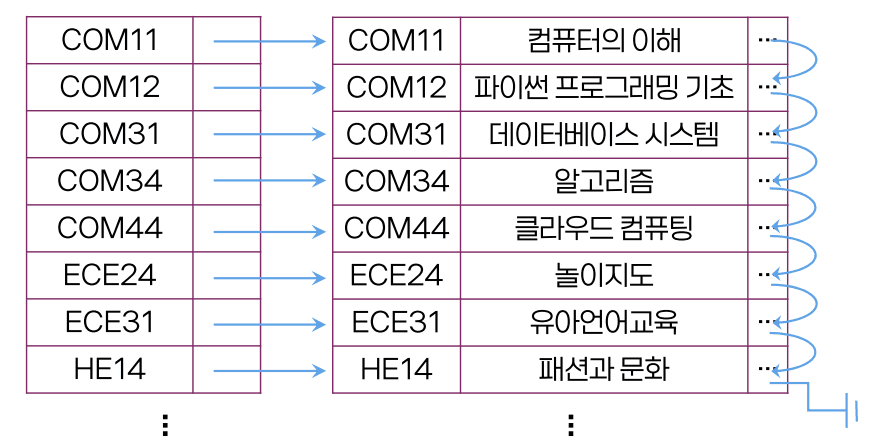
    image.png

  • 장점
    • 원하는 레코드를 빠르게 찾을 수 있음
  • 단점
    • 레코드 수만큼 인덱스 엔트리 존재
    • 인덱스의 크기가 방대해짐
    • 레코드가 많으면 조회 시 오랜 시간 소요

희소 인덱스(sparce index)

  • 인덱스의 엔트리가 일부의 탐색 키 값만을 유지
    • 가끔씩 존재하는 인덱스 엔트리
    • 요청 된 탐색 키보다 작거나 같은 인덱스의 탐색 키 값 중 가장 큰 인덱스 엔트리의 포인터가 가리키는 블럭을 스캔
      • 인덱스 엔트리가 만들어지지 않은 레코드를 찾는 방법

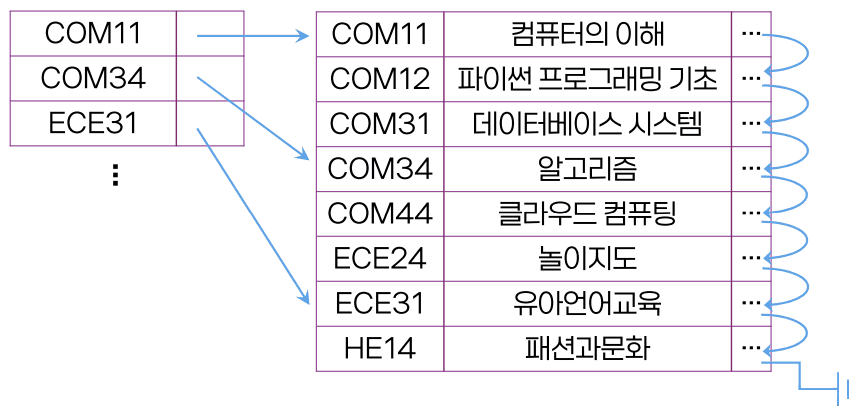
    image.png

  • 장점
    • 밀집 인덱스에 비해 작은 크기
      • 인덱스 메모리 적재 빠른 속도
  • 단점
    • 인덱스 엔트리에 없는 레코드를 찾아야 할 경우, 블록 내에서 재 검색 필요

다단계 인덱스의 필요

  • 4KB 크기의 한 블록에 100개의 엔트리가 삽입될 때, 100,000,000개의 레코드에 대한 밀집 인덱스
    • 1,000,000개의 블록 = 4GB의 공간 필요
  • 인덱스 크기에 따른 검색 성능
    • 인덱스 크기 > 메모리 크기
      • 저장된 블록을 여러 번 나누어 읽어야 하기 때문에 디스크 I/O 비용이 증가하여 탐색 시간이 증가
    • 인덱스 크기 < 메모리 크기
      • 디스크 I/O이 줄어 탐색 시간이 축소
  • 복수 계층의 인덱스를 구성

다단계 인덱스의 구조

  • 내부 인덱스와 외부 인덱스로 구성
    • 외부 인덱스를 내부 인덱스보다 희소한 인덱스로 구성하여 엔트리의 포인터가 내부 인덱스 블럭을 지칭

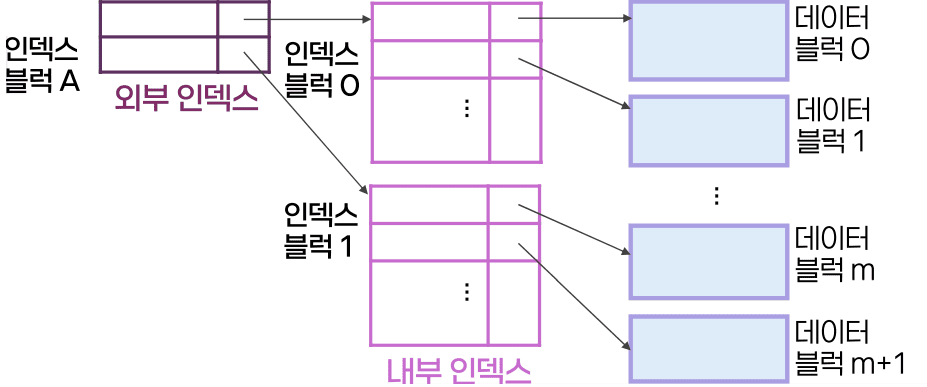
    image.png

B+ - 트리 인덱스

카드 찾기

  • 카드를 더 빨리 찾으려면?

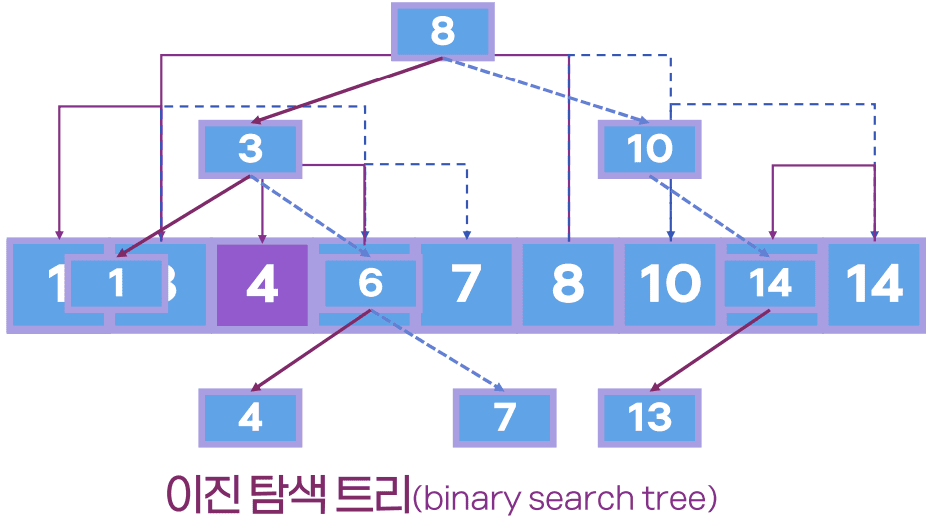
    image.png

  1. 탐색 키가 정렬되어 있으면 훨씬 더 빠르게 원하는 값을 찾을 수 있음
  2. 숫자끼리도 연결 고리를 만들어 줌
    • 포인터를 만들어 연결하면 더 빨리 찾을 수 있음 - B+트리 인덱스
    • 이진 트리 인덱스의 확장판

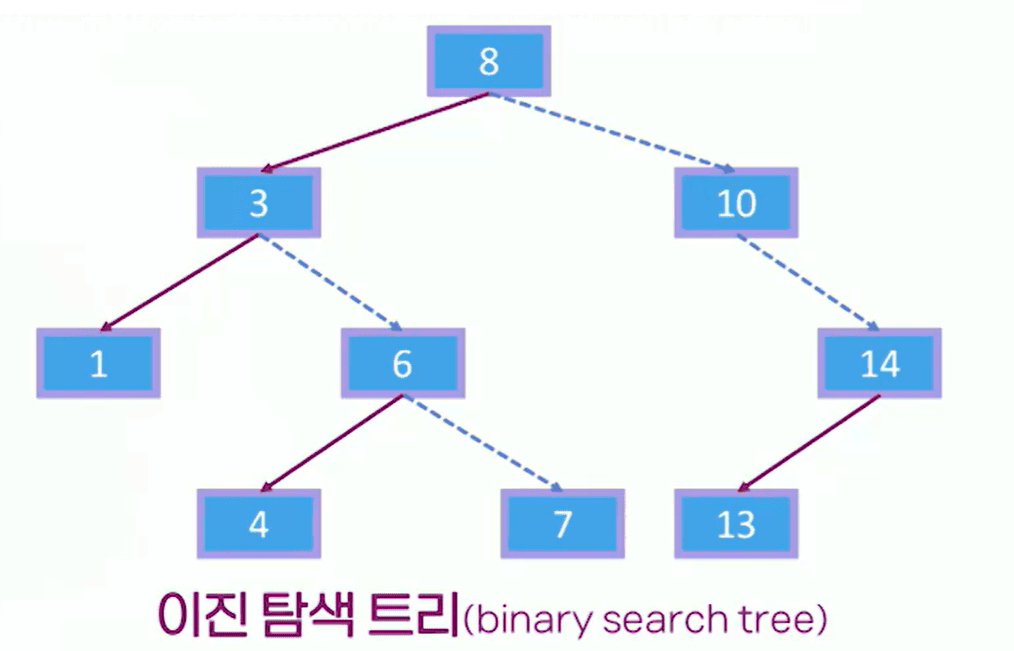
    image.png

    • 각 노드에 여러 개의 키 값을 넣는다면?

B+ - 트리의 구조

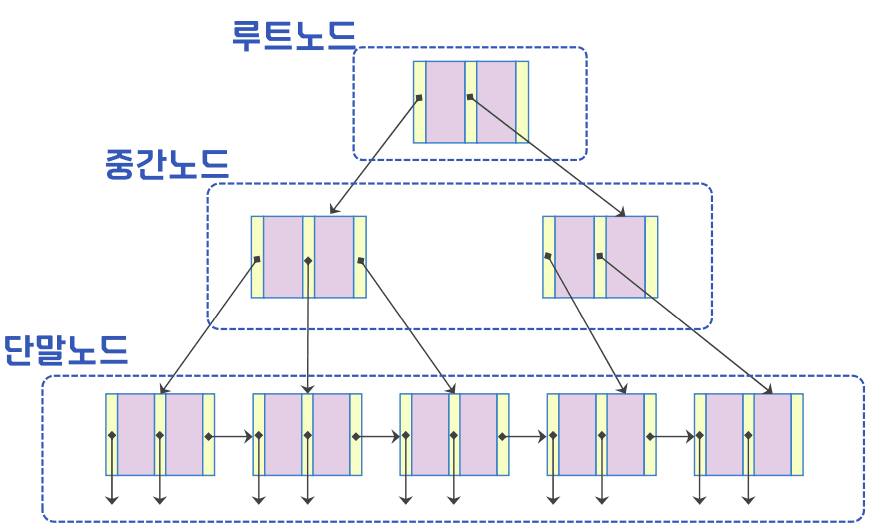
image.png

  • 데이터의 양이 많아져도 트리의 높이는 그리 안 커짐
  • 루트 노드부터 모든 단말 노드에 이르는 경로의 길이가 같은 높이 균형 트리
    • 순서 인덱스는 파일이 커질수록 데이터 탐색에 있어서 접근 비용이 커지는 문제점을 해결하기 위해 제안
    • 상용 DBMS에서도 널리 사용되는 대표적인 순서 인덱스

  • B+ - 트리의 노드 구조

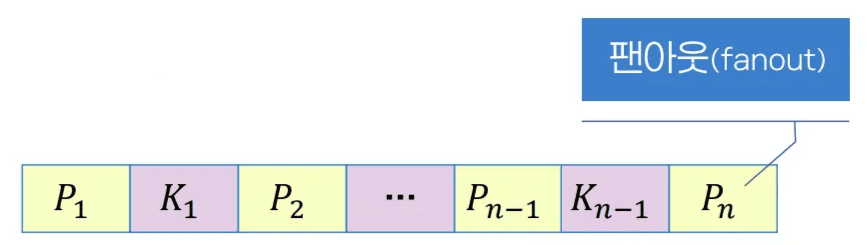
    image.png

    • 팬 아웃 값이 적으면 트리 높이가 커짐

B+ - 트리의 구성 요소

  • 인덱스 세트

    image.png

    • 루트 노드와 중간 노드로 구성
      • 단말 노드에 있는 탐색 키 값을 신속하게 찾아갈 수 있도록 경로를 제공하는 목적으로 사용
      • [n / 2] ~ n 사이의 개수를 자식으로 소유
        • 트리 높이가 커지지 않도록 제약
    • 중간 노드가 가리키는 범위에 가면 원하는 포인터를 찾을 수 있음
      • 힌트 제공

  • 순차 세트

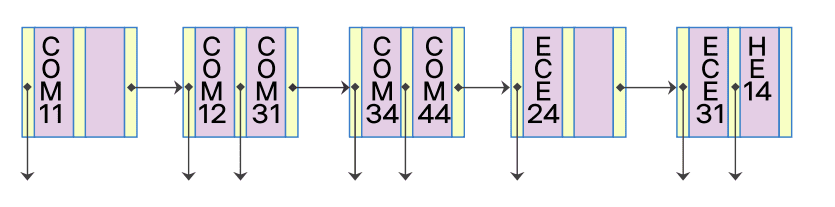
    image.png

    • 단말 노드로 구성
      • 모든 노드가 순차적으로 서로 연결
        • 실제 레코드의 포인터가 모여 있는 단말 노드
      • 적어도 [(n - 1)/ 2] 개의 탐색 키를 포함
      • 탐색 키에 대한 실제 레코드를 지칭하는 포인터를 제공
    • 왼쪽 → 오른쪽 노드로 신속히 접근 가능
    • 키 값과 같은 것은 왼쪽을 따라 가면 해당 레코드가 있는 곳 찾을 수 있음

단말 노드의 구성

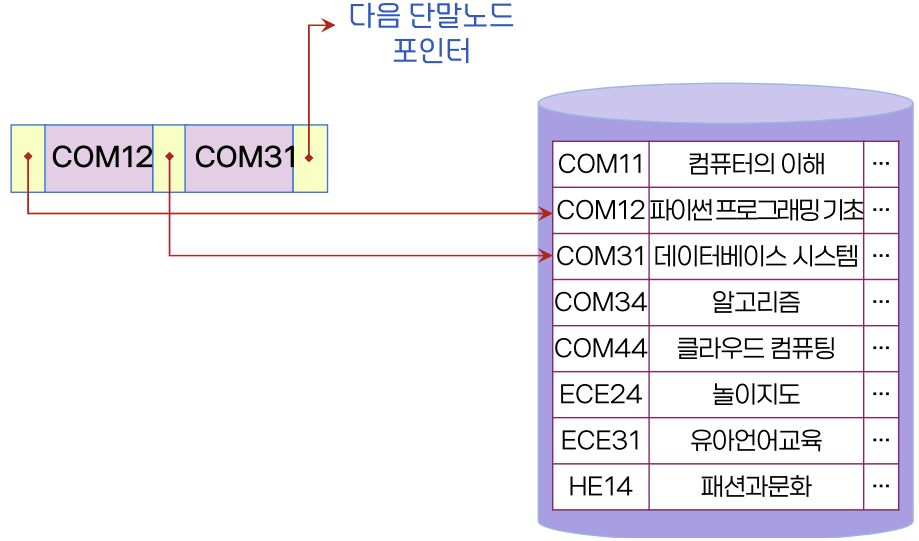
image.png

  • 인덱스 엔트리와 역할이 동일한 포인터

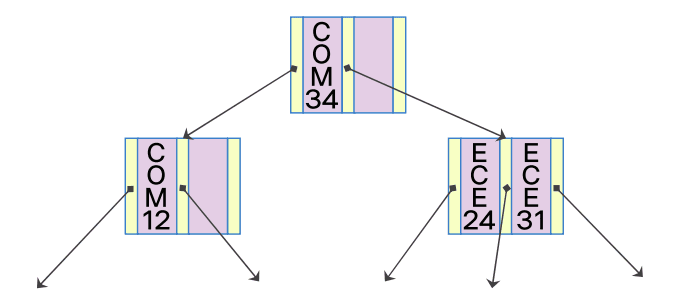
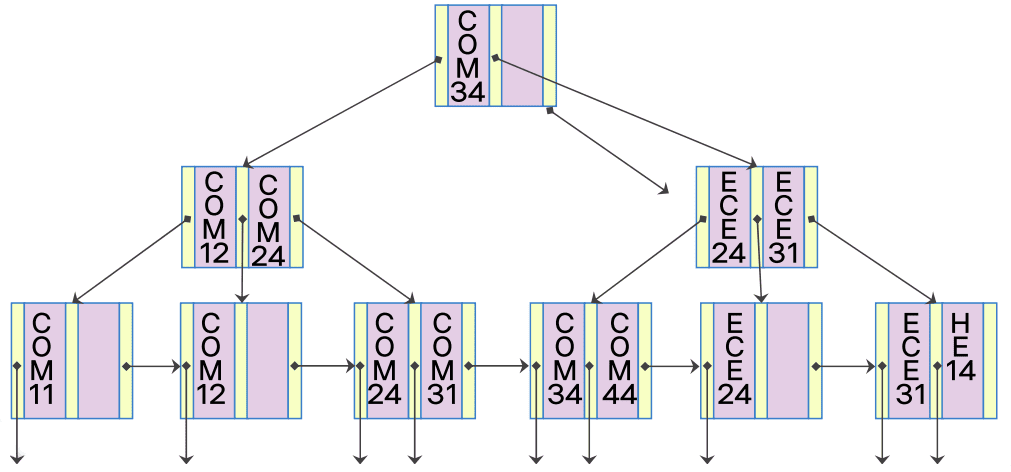
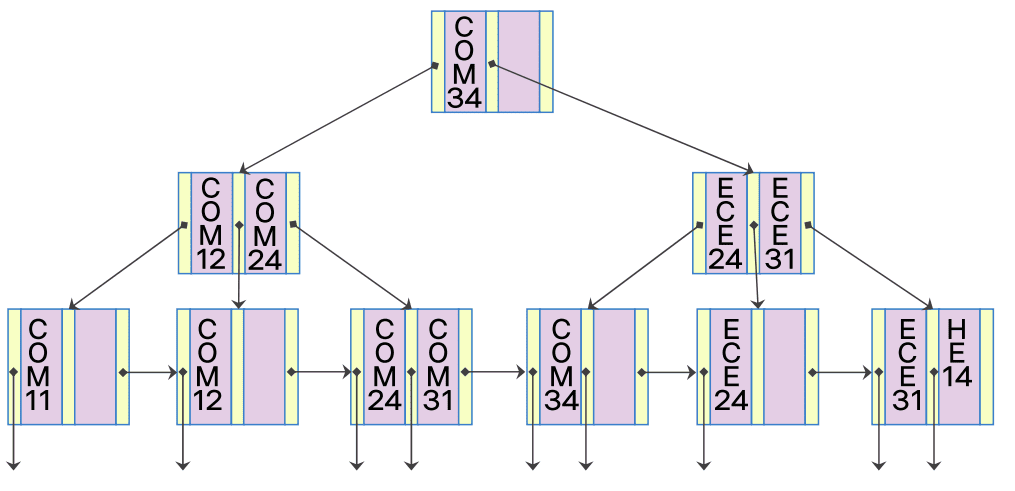
B+ - 트리의 예

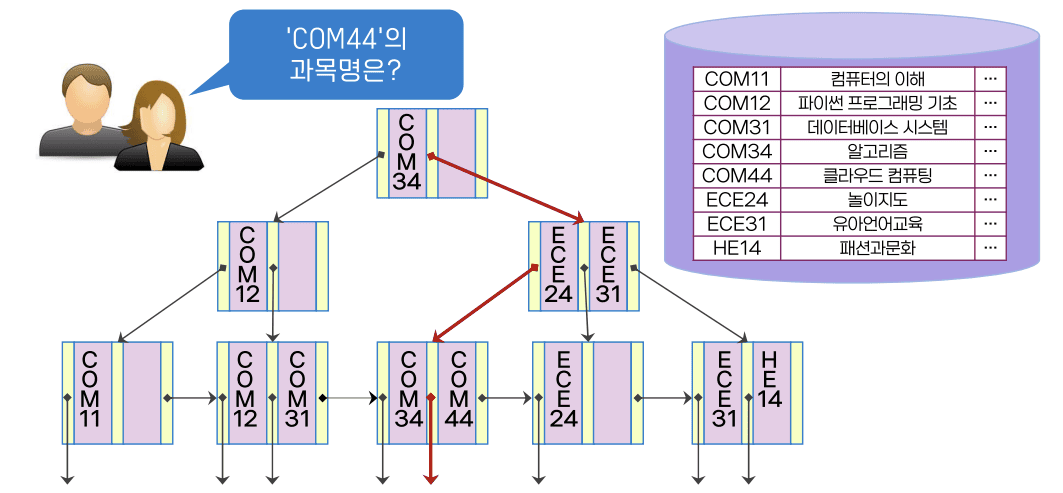
image.png

  • 세 단계의 노드 접근으로 원하는 정보 얻을 수 있음

B+ - 트리 상에서의 삽입, 삭제

  • 레코드 삽입, 삭제 시 B+-트리 수정
    • 레코드 삽입
      • 노드에서 유지해야 할 탐색 키와 포인터 수 증가로 인해 노드를 분할해야 하는 상황이 발생
    • 레코드 삭제
      • 노드에서 유지해야 할 탐색 키 값과 포인터 수 감소로 형제 노드와 키를 재분배 또는 병합해야 하는 상황이 발생
    • 높이 균형 유지
      • 노드가 분할 되거나 병합되면서 높이의 균형이 맞지 않는 상황이 발생

B+-트리 상에서의 삽입과 삭제

  • 삽입
    • 검색과 같은 방법을 사용하여 삽입되는 레코드의 탐색 키 값이 속할 단말 노드를 탐색
      • 해당 단말 노드에 <탐색키, 포인터> 쌍을 삽입
      • 삽입 시 탐색 키가 순서를 유지
  • 삭제
    • 삭제 될 레코드의 탐색 키를 통해 삭제될 탐색 키와 포인터를 포함한 단말 노드를 탐색
      • 같은 탐색 키 값을 가지는 다중 엔트리가 존재할 경우, 삭제될 레코드를 가리키는 엔트리를 찾을 때까지 탐색 후 단말 노드에서 제거
      • 단말 노드에서 제거된 엔트리의 오른쪽에 있는 엔트리들은 빈 공간이 없도록 왼쪽으로 이동
  • 레코드, 탐색 키 변화는 자동적으로 인덱스에도 영향을 끼침
  • 작은 값이 왼쪽, 큰 값이 오른쪽으로 정렬되도록 함

노드가 분할 되는 삽입

  • COM24 삽입

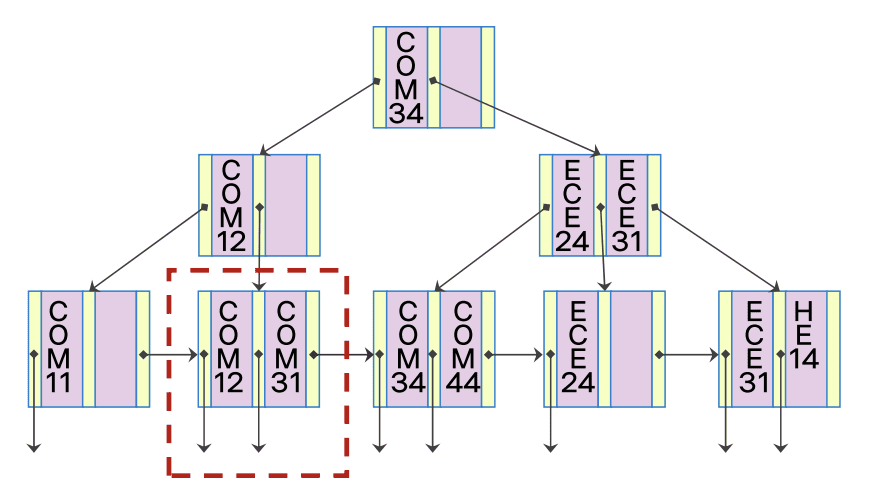
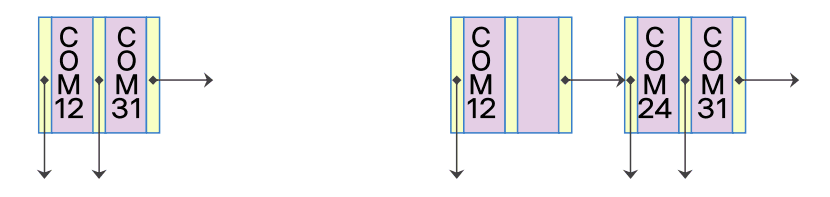
    image.png

    image.png

    • 삽입 대상 노드에 추가적인 저장할 공간 부족: 노드 분할
      • COM12를 하나의 단말 노드로 구성
      • COM24와 COM31이 하나의 단말 노드로 구성
    • 부모 노드에 탐색 키를 조정하고 추가 된 노드에 대한 포인터를 삽입

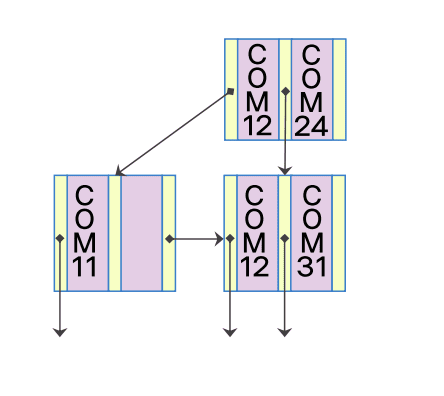
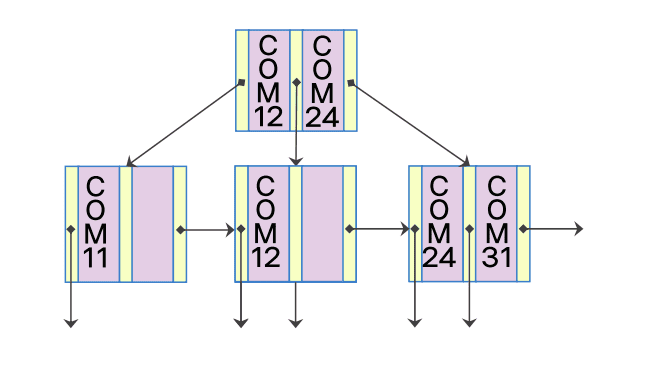
    image.png

    image.png

    image.png

탐색 키의 삭제

  • COM44 삭제

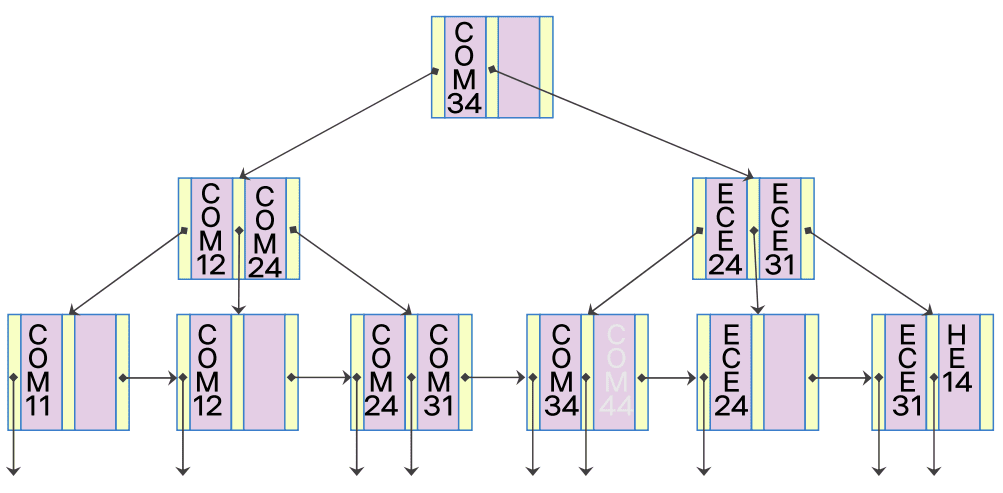
    image.png

  • COM12 삭제

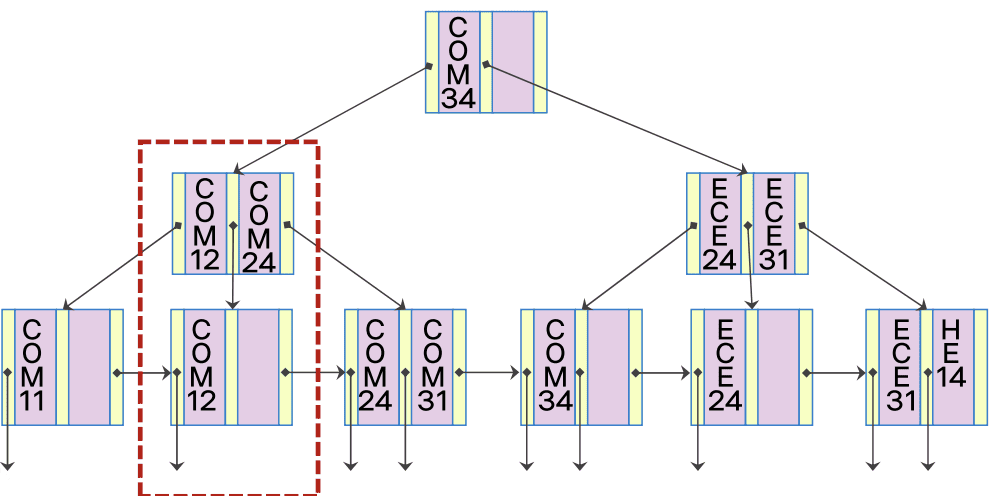
    image.png

탐색 키가 재분배 되는 삭제

  • COM12 삭제

    image.png

    • COM12가 있는 단말 노드를 검색하고 탐색 키를 삭제
      • 해당 단말 노드는 삭제 후 탐색 키가 존재하지 않음
      • [(n - 1) / 2]개 보다 탐색 키가 적으므로 다른 노드와 별도의 재구조화 작업이 필요

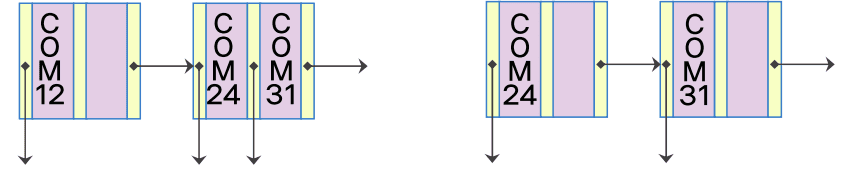
    • COM12가 저장된 노드의 오른쪽의 형제 노드와 키를 재분배

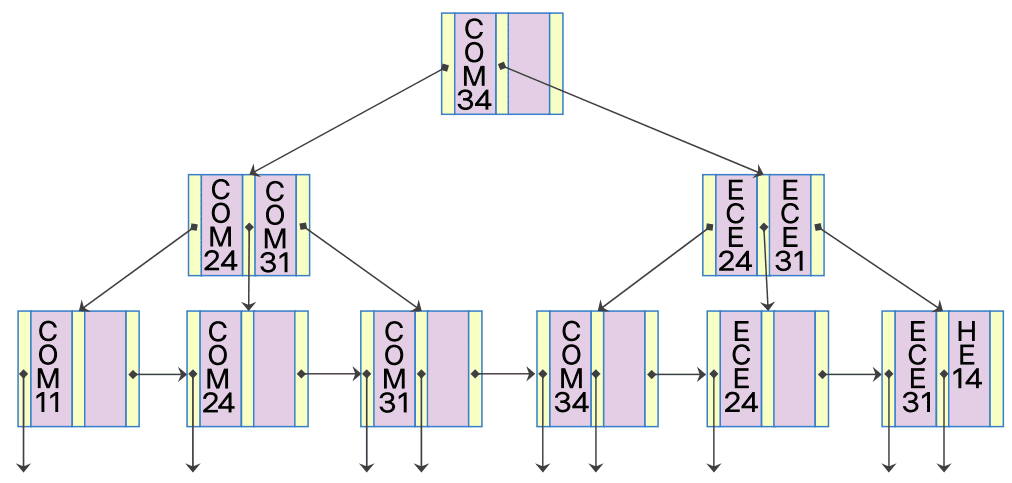
      image.png

      image.png

      • 가장 작은 탐색 키 값 COM24를 중간 노드로 재구조화



연습 문제

  1. 다음 중 요청된 레코드에 빠르게 접근할 수 있도록 하는 구조인 인덱스의 효율성에 대한 평가 기준이 아닌 것은?

    a. 사용자가 질의에 사용할 조건을 자유롭게 지정할 수 있는 정도

    • 사용자가 질의 조건을 자유롭게 지정할 수 있는 정도는 질의 언어(SQL)나 인터페이스 표현력과 관련 된 요소로, 인덱스 구조의 효율성과는 직접적인 관련이 없음
    • 인덱스의 효율성에 대한 평가 기준
      • 새로운 데이터 삽입 시 발생하는 인덱스 구조 유지 비용
      • 인덱스를 통해 데이터를 찾고 접근하는데 걸리는 시간
      • 인덱스를 저장하기 위해 부가적으로 필요한 공간 비용

  2. 다음의 설명은 어떤 인덱스에 대한 설명인가?

    1

     모든 탐색키 값에 대해 탐색키 <값, 포인터> 쌍으로 구성된 인덱스 엔트리를 갖고, 인덱스 파일의 크기가 커서 I/O 비용이 증가하여 탐색 시간이 오래 걸릴 수 있는 단점을 지님

    a. 밀집 인덱스

    • 밀집 인덱스와 같이 모든 탐색 키 값에 대하여 탐색 키를 갖게 되면 인덱스가 메모리에 상주할 수 있는 정도의 크기라면, 추가적인 I/O 비용의 발생이 없이 원하는 데이터를 찾을 수 있음
    • 하지만 모든 레코드의 탐색 키를 사용하여 인덱스를 생성하면 데이터의 크기가 커질 수록 밀집 인덱스도 커지게 되어 메모리에 모두 적재되지 못하여 인덱스를 탐색하면서 추가적인 I/O 비용이 발생할 수 있음
    • 따라서 인덱스의 크기를 줄이기 위해 일부의 탐색 키만을 사용하여 인덱스인 희소 인덱스를 사용하기도 하고 다단계 인덱스를 사용하기도 함

  3. 다음은 B+ 트리의 예시이다. ‘이순신’을 탐색하는 과정에서 거치는 포인터를 올바른 순서로 나열한 것은?

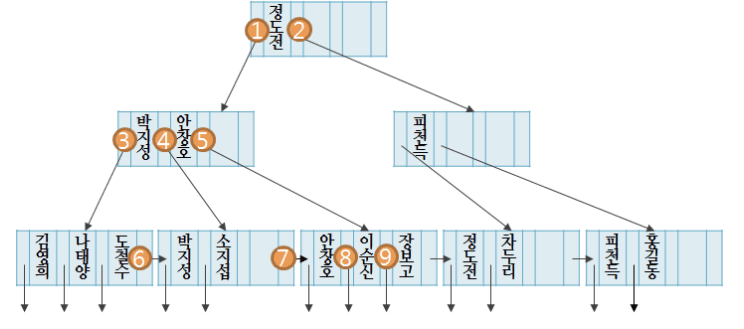
    image.png

    a. 1, 5, 8

    • 이순신을 탐색하기 위해 루트 노드에 있는 정도전과 비교하여 사전 순서로 정도전보다 값이 작은 것을 알 수 있음
    • 따라서 1번 포인터를 타고 왼쪽의 자식 노드에 접근함
    • 그 다음 박지성과 안창호를 비교했을 때, 박지성과 안창호보다 이순신의 값이 큰 것을 알 수 있음
    • 따라서 5번 포인터로 오른쪽 자식 노드에 접근하여 최종적으로 이순신의 왼쪽에 저장 된 8번 포인터를 통하여 디스크에 저장 된 이순신 레코드에 접근하게 됨



정리 하기

  • 데이터베이스 시스템에서는 데이터에 대한 빠른 탐색을 지원하기 위해 인덱싱과 해싱을 이용함
  • 인덱스는 데이터 파일에 대한 빠른 탐색을 지원하는 부가적인 자료구조이며 인덱스를 생성하는 작업을 인덱싱이라고 함
  • 탐색 키의 순서로 정렬된 순차 파일에서는 데이터 레코드에 대한 빠른 임의 접근이 가능 하도록 순서 인덱스를 사용할 수 있음
  • 인덱스는 모든 레코드에 대하여 인덱스 엔트리를 구성하는 밀집 인덱스와, 일부 레코드에 해당하는 인덱스 엔트리를 사용하여 인덱스를 구성하는 희소 인덱스, 밀집 인덱스와 희소 인덱스의 개념을 모두 사용한 다단계 인덱스로 구분할 수 있음
  • B+–트리 인덱스는 루트에서 단말(leaf) 노드까지 모든 경로의 길이가 같은 높이 균형 트리로 트리에서 단말 노드나 루트 노드가 아닌 중간(internal) 노드는 [n / 2]과 n 사이의 자식을 갖는 대표적인 인덱스 구조임
  • B+–트리를 활용한 특정 탐색 키 탐색은 루트부터 시작해서 단말 노드에 도달할 때까지 비교 연산을 하며 이루어짐
    • 말단 노드에 도착하면 탐색이 종료 됨
  • 새로운 레코드의 삽입과 삭제 시, B+–트리는 재 구조화 됨
    • B+–트리 구조의 생성 조건을 유지 시키기 위해 인덱스 엔트리 삽입과 삭제 시 노드의 분할 및 노드의 병합이 이뤄짐



체크 포인트

  1. 데이터베이스의 인덱스와 관련한 설명으로 틀린 것은? a. 인덱스의 추가, 삭제 명령어는 각각 ADD, DELETE이다.

    • 인덱스는 데이터베이스 객체이기 때문에 CREATE, DROP 명령어 사용함
    • 인덱스와 관련 된 설명으로 옳은 것
      • 문헌의 색인, 사전과 같이 데이터를 쉽고 빠르게 찾을 수 있도록 만든 데이터 구조임
      • 테이블에 붙여진 색인으로 데이터 검색 시 처리 속도 향상에 도움이 됨
      • 대부분의 데이터베이스에서 테이블을 삭제하면 인덱스도 같이 삭제 됨

  2. B+-트리 인덱스에 대한 설명으로 옳은 것만을 모두 고르면?

    1
2
3

     ㄱ. 루트(root)를 포함한 내부 노드(internal node)는 데이터 파일 레코드를 가리키는 포인터를 갖는다.
 ㄴ. 트리의 루트에서 단말 노드(leaf node)까지 모든 경로의 길이가 같은 균형 트리(balanced tree) 형태이다.
 ㄷ. 단말 노드는 검색 키 값을 기초로 선형 순서로 되어 있어 데이터 레코드들을 그 키 값의 순서에 따라 능률적으로 순차 접근할 수 있게 해 준다.

    a. ㄴ, ㄷ

    • 트리의 루트에서 단말 노드(leaf node)까지 모든 경로의 길이가 같은 균형 트리(balanced tree) 형태임
    • 단말 노드는 검색 키 값을 기초로 선형 순서로 되어 있어 데이터 레코드들을 그 키 값의 순서에 따라 능률적으로 순차 접근할 수 있게 해줌
Knou, 데이터베이스 시스템
knou database
Recently Updated
Contents

[데이터베이스 시스템] 10강 - 데이터 저장과 파일

[파이썬 프로그래밍 기초] 11강 - 모듈