[데이터베이스 시스템] 12강 - 해싱과 특수 인덱스

💡해당 게시글은 방송통신대학교 정재화 교수님의 '데이터베이스 시스템' 강의를 개인 공부 목적으로 메모하였습니다.

학습 개요

---

• DBMS에서 인덱스는 조건에 부합하는 레코드를 빠르게 탐색할 수 있도록 돕는 보조적 구조이며, 일반적으로는 B+-트리가 가장 널리 사용 됨
• B+-트리는 범위 질의나 정렬된 데이터 접근에 효과적이지만, 모든 질의 유형에 대해 항상 최상의 성능을 보장하지는 않음
• 특히 일치 검색을 반복적으로 수행하거나, 특정 조건에 대해 검색 효율을 높여야 하는 경우에는 B+-트리보다 다른 구조가 적합할 수 있음
• DBMS 운용 시 다양한 인덱스 기법을 상황에 맞게 선택하여 활용하는 것이 필요함
• 해시 함수를 기반으로 하는 인덱싱 방식인 해싱(hashing) 기법을 중심으로 살펴봄
• 해싱은 특히 등가 조건에 대한 빠른 탐색에 효과적인 방법이며, 정적 해싱과 동적 해싱을 포함한 다양한 기법이 존재함
• 속성의 도메인이 제한적인 경우에 대량의 읽기 기반 질의에서 공간 효율성과 성능 측면에서 유리한 특성을 갖는 특수한 인덱싱 구조인 비트맵 인덱스(bitmap index)에 대해서도 함께 학습함

주요 용어

---

• 해시 함수
  • 레코드의 탐색 키에 따라 레코드를 버킷에 대응 시키기 위해 사용하는 함수
• 버킷
  • 한 개 이상의 레코드를 저장할 수 있는 저장 공간 단위
• 충돌
  • 서로 다른 레코드가 같은 버킷 주소로 대응되는 상황
• 오버 플로
  • 버킷에 레코드를 저장할 수 있는 충분한 여유 공간이 없는 상태
• 비트맵
  • 주어진 릴레이션에 존재하는 레코드의 수 만큼의 비트로 특정 컬럼 값의 유무를 표현한 비트 열

강의록

---

해싱의 이해

해싱의 개념

• 해시(hash)

• 탐색 키에 산술적인 연산을 통해 버킷의 주소를 계산하는 해시 함수를 사용하여 데이터 배분 및 접근하는 기법

  

• 버킷(bucket)
  • 한 개 이상의 레코드를 저장할 수 있는 저장 공간의 단위
  • 일반적으로 버킷의 크기는 디스크 블록의 크기와 일치

해시의 구조

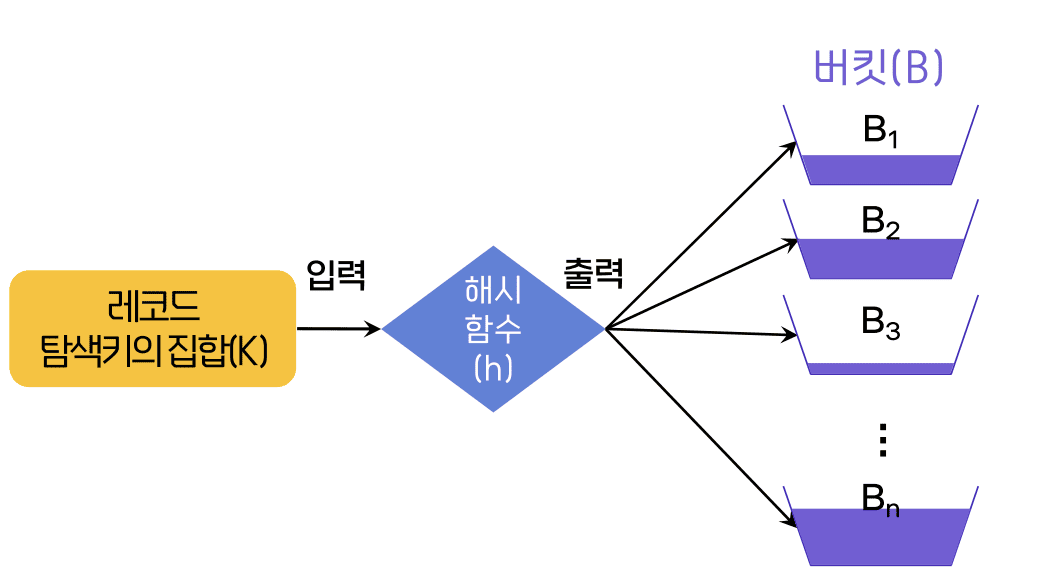
해시의 사용

• h(K₃) = h(K₇) = 3

  

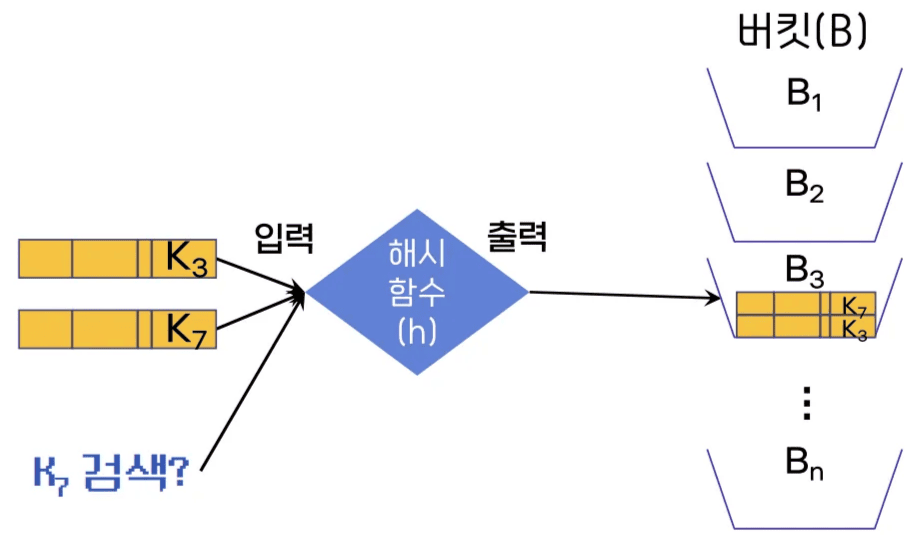
해시 함수의 역할

• 최상의 경우

  

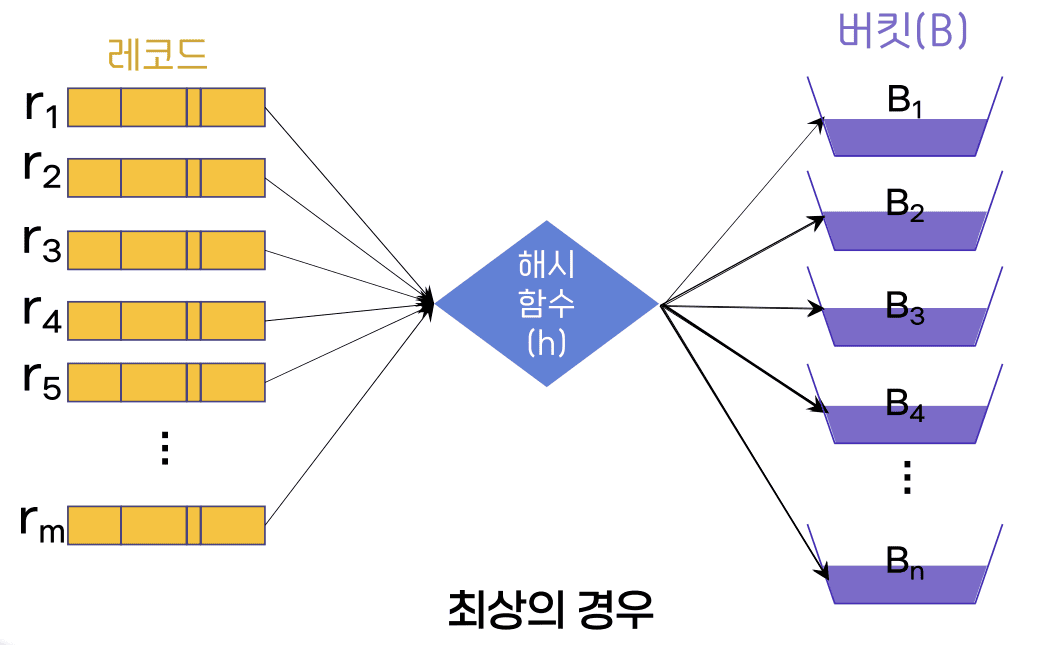
  • 균등하고 예쁘게 저장
    • 각각의 버킷에 담겨 있는 레코드의 수는 최소화 되고 버킷내에서 특정 레코드를 찾을 때 훨씬 적은 시간 소요 됨

• 최악의 경우

  

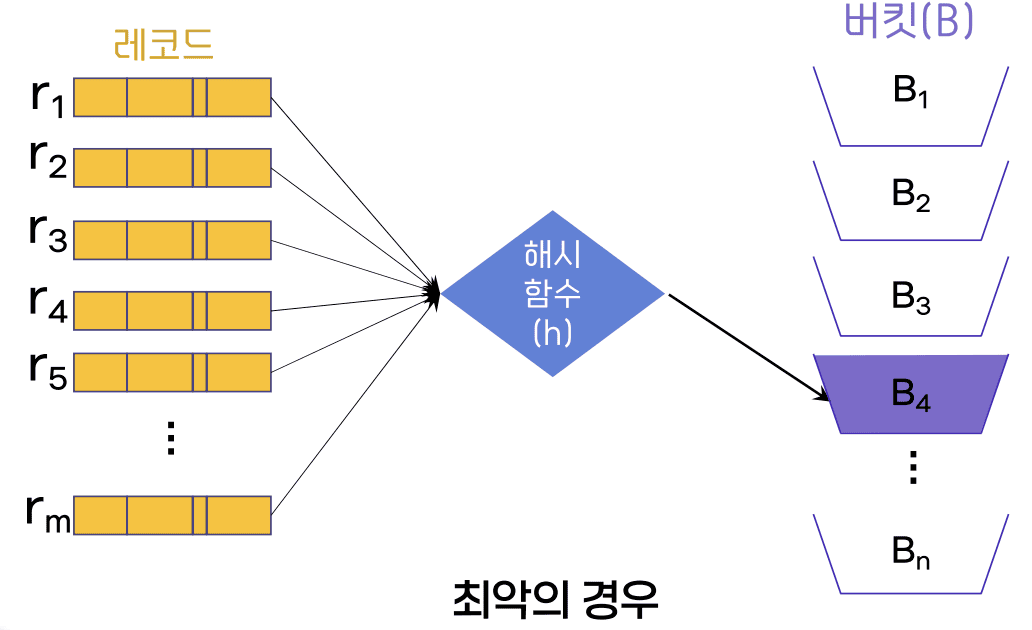
  • 나머지 버킷 낭비
    • 버킷 내에서 특정 레코드를 찾을 때 많은 시간 소요 됨

• 일반적인 경우

  

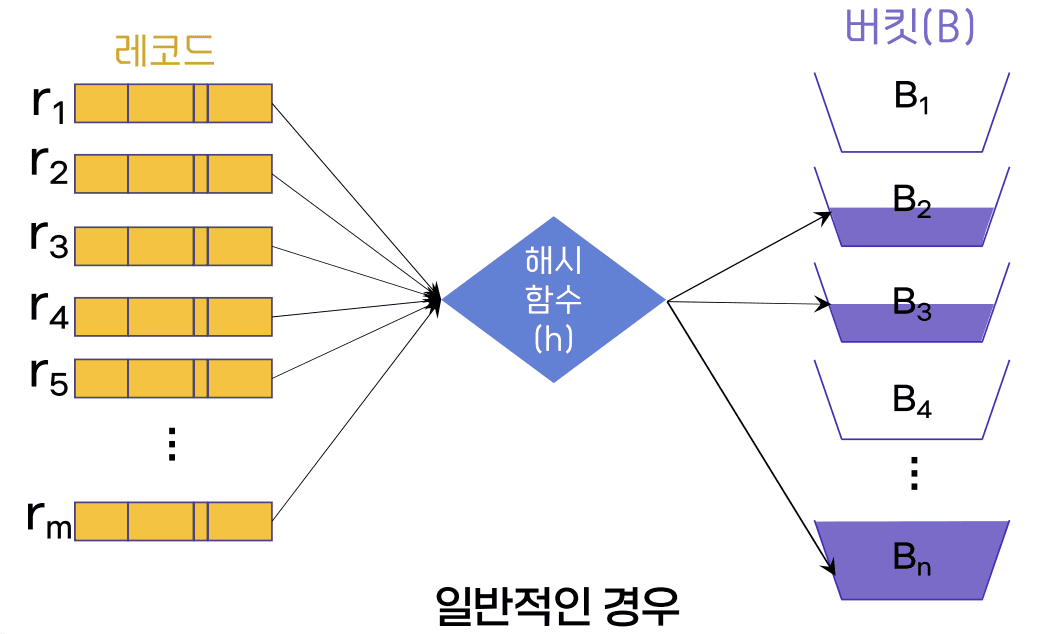
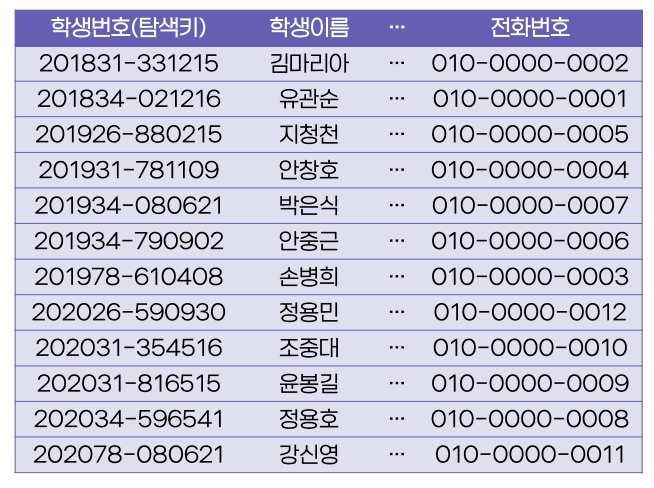
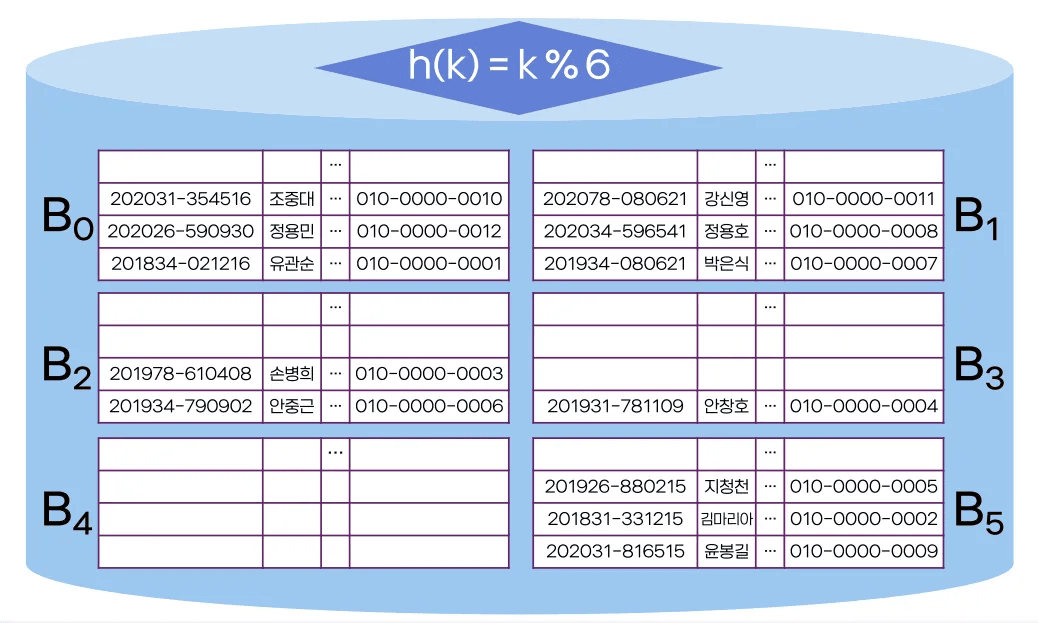
해시 파일 구조

• 학번의 마지막 자릿수를 6으로 나눈 나머지로 해시 함수를 정의
  • 해시 함수로 어떻게 구조화 하는 지를 아는 것이 중요

  

  

정적 해싱의 특징

• 버킷의 개수가 고정 된 해싱 기법
  • 해시 함수로 키 값이 어떻게 유지 되는지를 파악하는 것이 중요
• 키 값이 Kᵢ인 레코드 삽입
  • h(Kᵢ)를 통하여 Kᵢ에 대응하는 버킷 주소를 생성하고 레코드를 해당 버킷에 저장
    • 인덱스 엔트리를 버킷에 저장한다면 더 빠른 검색이 가능
  • 키 Kᵢ를 가진 데이터를 저장할 때, 해시 함수 h(Kᵢ)로 해시 값을 계산하고 해당 버킷에 데이터를 저장함
    • 데이터 키: Kᵢ = 25
    • 해시 함수: h(Kᵢ) = Kᵢ % 10
    • 결과: h(25) = 25 % 10 = 5 → 데이터를 버킷 5번에 저장
• 키 값이 Kᵢ인 레코드 검색
  • h(Kᵢ)을 통하여 버킷 주소를 생성하고 버킷에 저장 된 레코드 접근
  • h(Kᵢ) = h(Kⱼ) = m인 경우가 발생하기 때문에 버킷 m에 저장 된 모든 레코드를 탐색하여 선택하는 과정이 필요
  • 키 Kᵢ로 저장된 데이터를 찾으려면, 해시 함수 h(Kᵢ)를 적용하여 해당 주소를 찾음
    • 검색 키: Kᵢ = 25
    • 해시 함수: h(Kᵢ) = Kᵢ % 10
    • 결과: h(25) = 25 % 10 = 5 → 버킷 5번에서 데이터를 읽음

충돌과 동거자

• 같은 버킷 아이디가 나왔을 때 사용하는 용어들
• 해시 함수는 때때로 다른 탐색 키에도 같은 버킷 주소를 내보냄
  • 탐색 키는 다르지만 같은 버킷에 있음
• 충돌
  • 서로 다른 두 레코드가 동일한 버킷에 대응
  • 충돌은 서로 다른 상황에서 발생하기 때문에 균등하게 데이터가 배분되기 보다 불균형이 생겨 버킷 id마다 서로 다른 갯수의 레코드가 저장될 수 있음
• 동거자
  • 충돌에 의해 같은 버킷 주소를 갖는 레코드

  

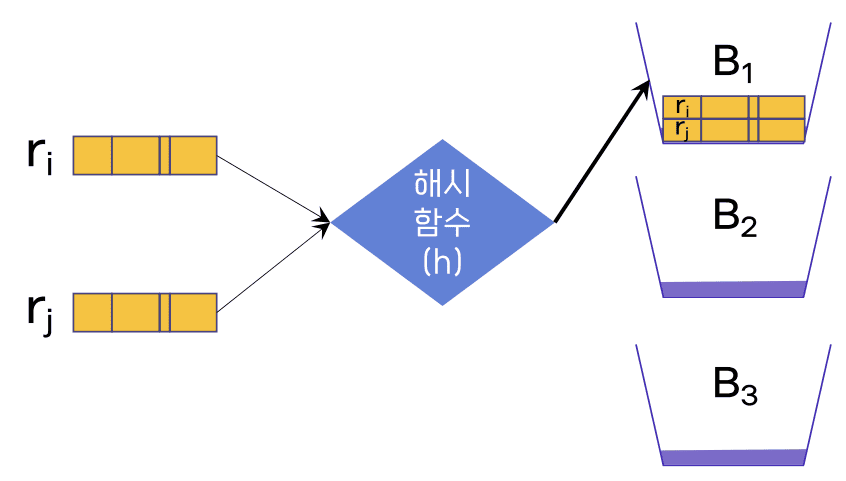
  • h(rᵢ) = h(rⱼ)

오버플로우(overflow)

• 버킷에 레코드를 저장할 수 있는 여유 공간이 없는 상황에 발생
• 추가적인 버킷 또는 다음 버킷에 할당하여 처리
• 오버플로우가 발생할 수록 접근 시간이 증가하고 해시 성능이 저하
  • 오버플로우 버킷에 추가적인 디스크 접근을 요구하므로 검색의 성능이 저하될 수 있음

  

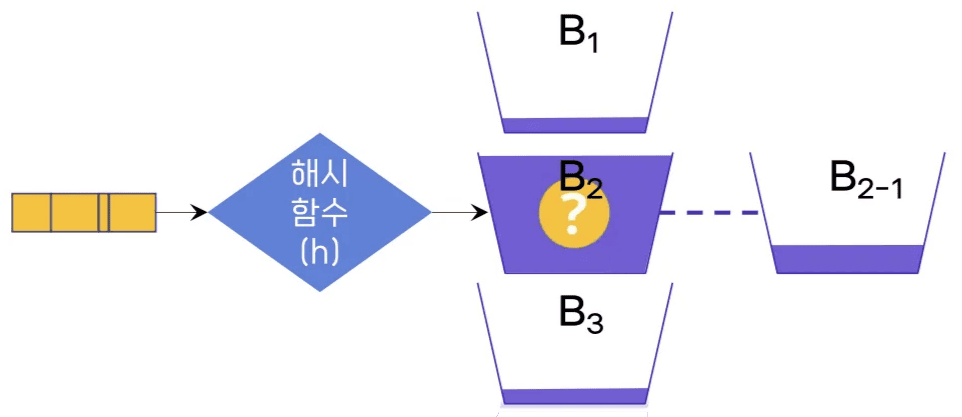
• 오버플로우 처리 방법
  1. 다음 아이디에 해당 레코드 저장
  2. 해당 버킷에 추가적으로 공간 할당
• 균등한 분배를 할 수 있도록 설계하는 것이 관건

해시 인덱스

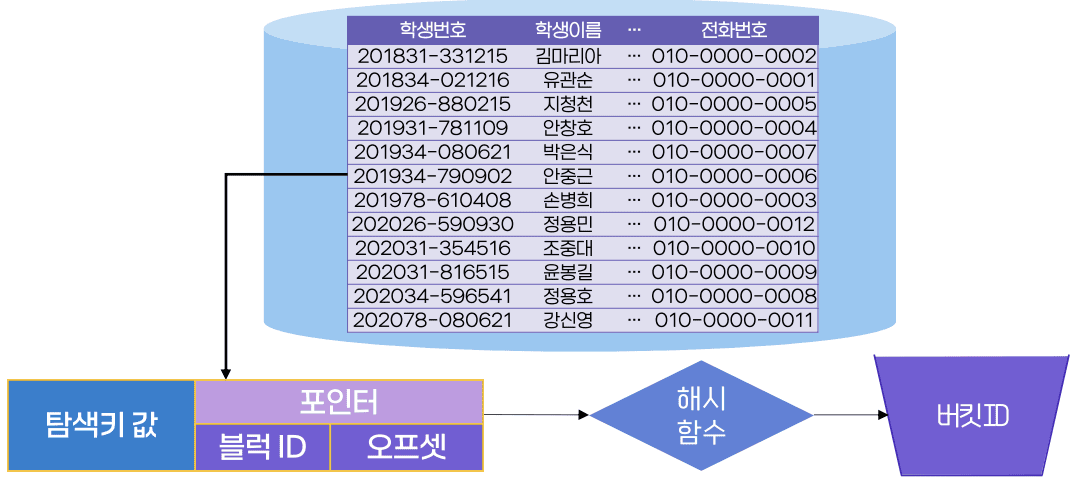
• 해시 파일 구조의 동작 방식을 레코드가 아닌 인덱스 엔트리에 적용한 인덱스

  

  

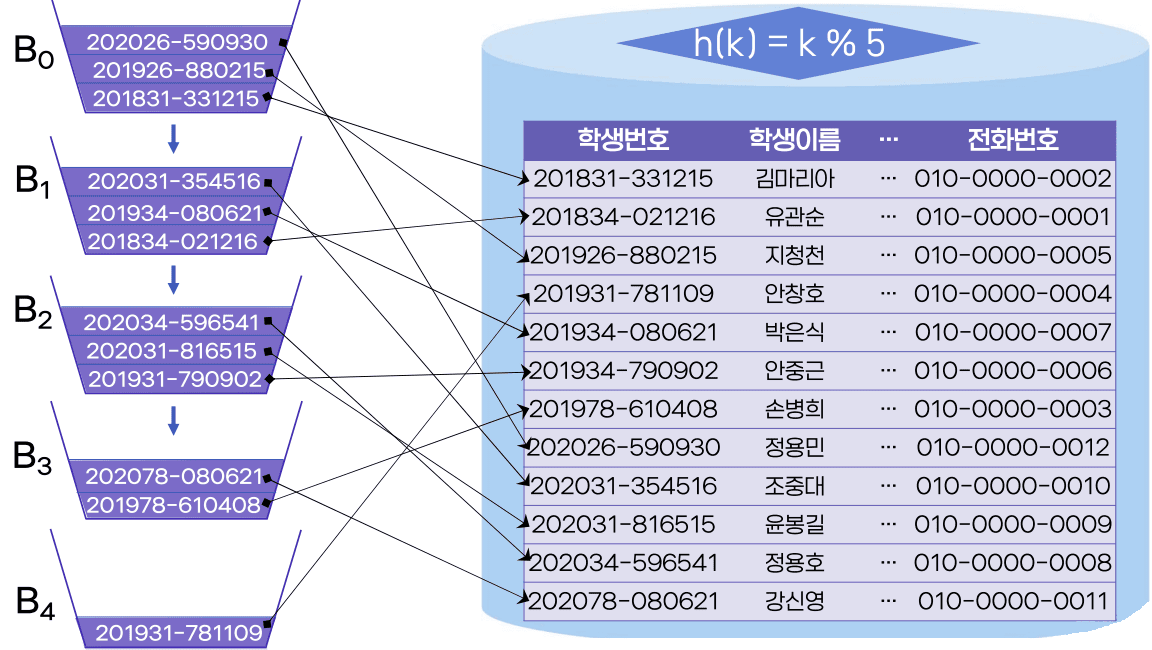
정적 해싱의 문제

• 데이터베이스의 크기가 커짐에 따른 성능 감소
• 사전에 큰 공간을 잡을 경우 초기에 상당한 양의 공간이 낭비
• 재구성 시 새롭게 정의 된 해시 함수를 사용하여 모든 인덱스 엔트리에 대하여 다시 계산하고 버킷에 재 할당하는 대량의 비용이 발생
  • 해시 구조의 크기가 동적으로 결정 되는 동적 해싱 기법 제안

동적 해싱

동적 해싱의 개념

• 동적 해싱의 정의
  • 버킷의 개수를 가변적으로 조절할 수 있는 해싱 기법
  • 데이터베이스의 크기에 따라 버킷의 크기가 비례
• 데이터베이스의 증대 혹은 축소에 따른 인덱스의 구조를 조절하기 위해 해시 함수를 동적 변경하는 기법
• 확장성 해싱
  • 동적 해싱의 일종으로 디렉터리와 버킷의 2단계 구조
  • 디렉터리는 디스크에 저장되는 버킷 주소 테이블
  • 디렉터리 깊이를 의미하는 정수 값 d를 포함하는 헤더와 데이터가 저장 된 버킷에 대한 2ᵈ개의 포인터로 구성

확장성 해싱

• 모조 키(pseudo key)
  • 레코드 탐색 키 값이 해시 함수에 의해 일정 길이의 비트 스트링으로 변환 된 키
  • 모조 키의 첫 d 비트를 사용하여 디렉터리에 접근
  • 해시 함수가 탐색 키를 모조 키로 만드는 역할을 함
• 버킷 헤더
  • 정수 값 i(≤ d)가 저장 되어 있음을 표시
  • i는 버킷에 저장되어 있는 레코드의 모조 키들이 처음부터 i 비트까지 일치함을 표시

확장성 해싱의 구조

• 데이터가 많아질 때, 디렉터리와 버킷 구조를 동적으로 확장함으로써 충돌 문제를 해결
  • 모조 키(pseudo key):
    • 해시 함수 h를 통해 탐색 키(key)를 일정 길이의 비트 스트링으로 변환
    • 모조 키는 해싱 결과의 비트 스트링
      • ex) 키 값 Kᵢ → h(Kᵢ) → 11001101
  • 디렉터리
    • 버킷에 접근하기 위한 “주소 목록” 역할
    • 최상위 d 비트(탐색 키의 앞부분)를 사용하여 실제 저장소(버킷)에 대한 주소를 관리
    • 디렉터리는 2^d개의 엔트리를 가짐
      • d는 디렉터리 깊이
  • 버킷
    • 실제 데이터를 저장하는 공간
    • 버킷 내에 존재하는 모든 레코드들은 공통적으로 탐색 키의 상위 i비트까지가 동일
      • 이 정보를 버킷 헤더(bucket header)에 기록해서 관리

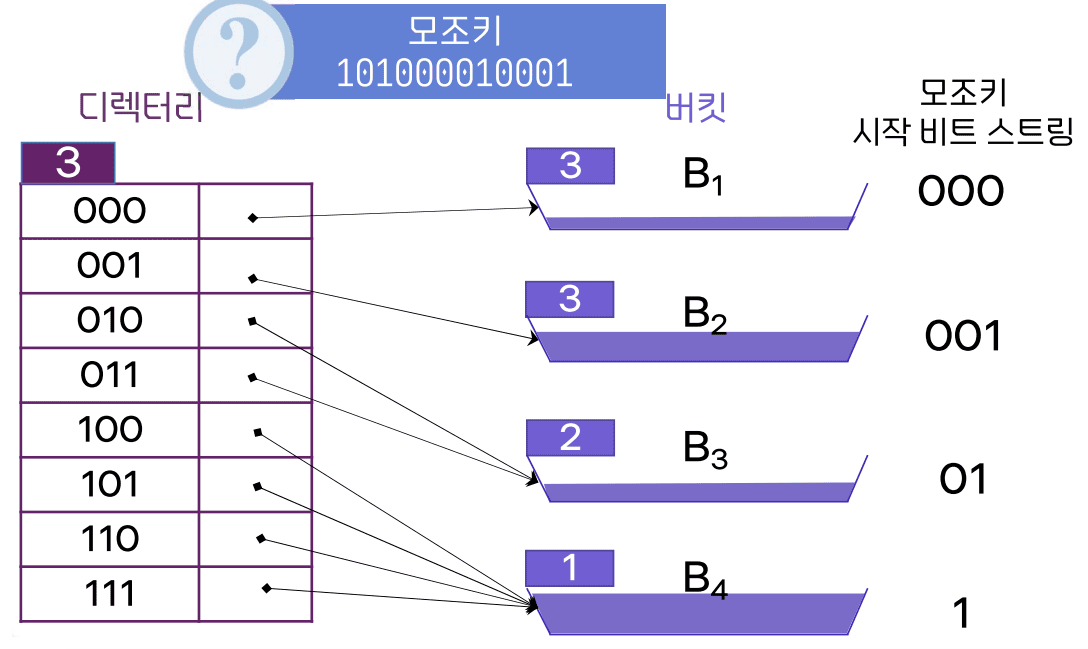
• 전체 모조 키 중 앞 3자리는 버킷의 위치를 알려주는 이정표
• 인덱스 엔트리 검색 → 레코드 접근 → 레코드를 메모리에 적재
• B4가 꽉찬 상태

확장성 해싱의 분할

• 레코드 삽입에 의해 분할 된 확장성 해싱 파일

  

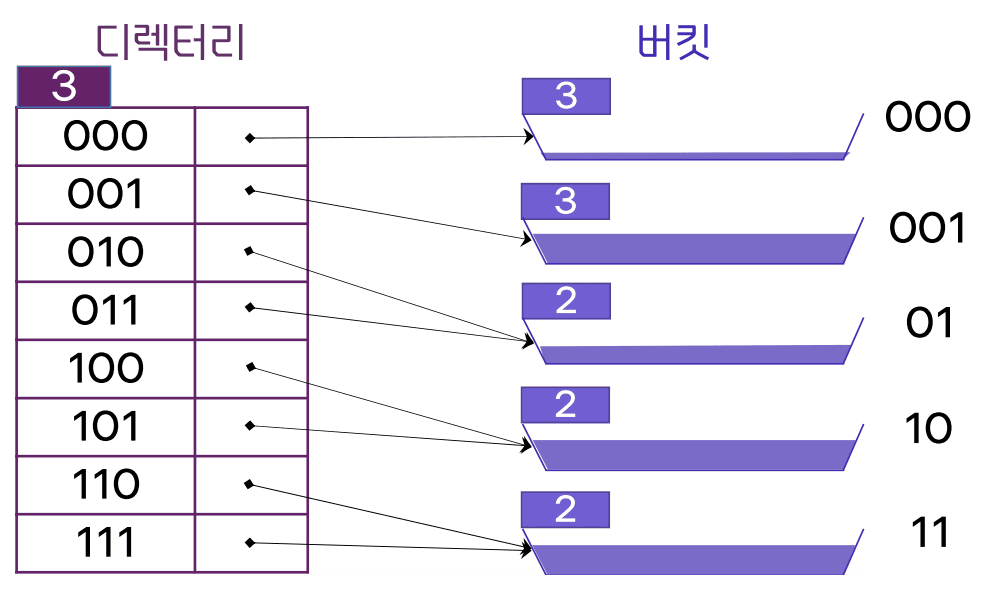
  • 추가적인 할당을 통해 재분배를 하는 확장성 해싱
  • 포인터 재분배

비트맵 인덱스

비트맵 인덱스의 개념

• 탐색 키의 중복 비율이 높은 컬럼을 대상으로 하는 질의를 효율적으로 처리하기 위해 고안 된 특수한 형태의 인덱스
  • B+- 트리 상에서 탐색 키 삽입, 삭제 했던 개념과 유사
  • 중복이 많은 컬럼은 비트맵 인덱스를 권장
    • 중복이 많은 컬럼 값에 적용하게 되면 레코드의 개수가 길어진다하더라도 비트맵도 길어지기 때문에 비트 논리곱 연산이 빠르게 수행 가능
• 비트맵
  • 간단한 비트의 배열
  • 릴레이션 r의 속성 A에 대한 비트맵 인덱스는 A가 가질 수 있는 값에 대해 비트맵을 구성
  • 각 비트맵은 릴레이션에 있는 레코드의 수 n개 만큼 n개의 비트로 표현

비트맵 인덱스 구성

• i번째 레코드가 컬럼 A에 해당 값을 가지면 비트 맵의 i번째 비트를 1로, 그렇지 않으면 0으로 설정

  

  

  

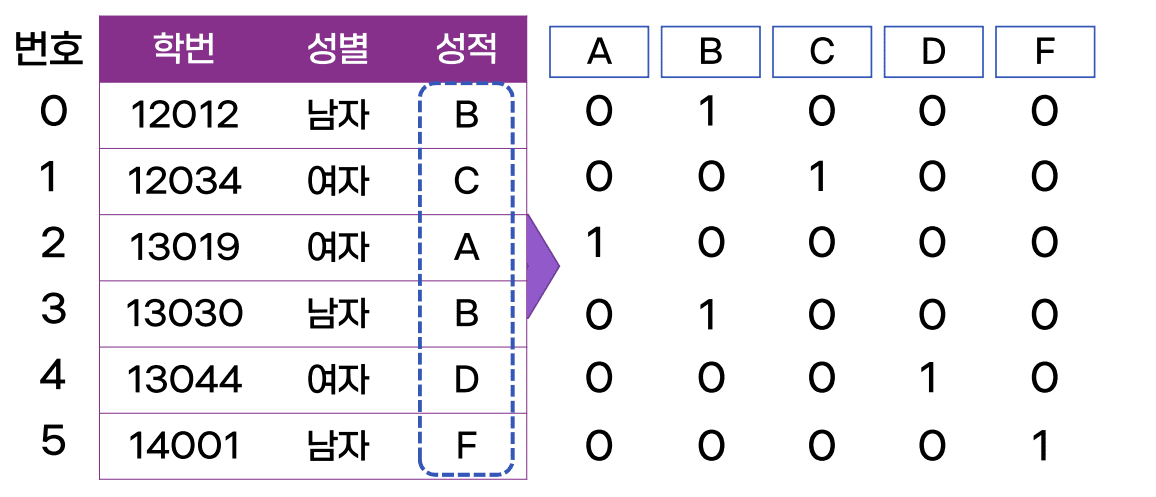
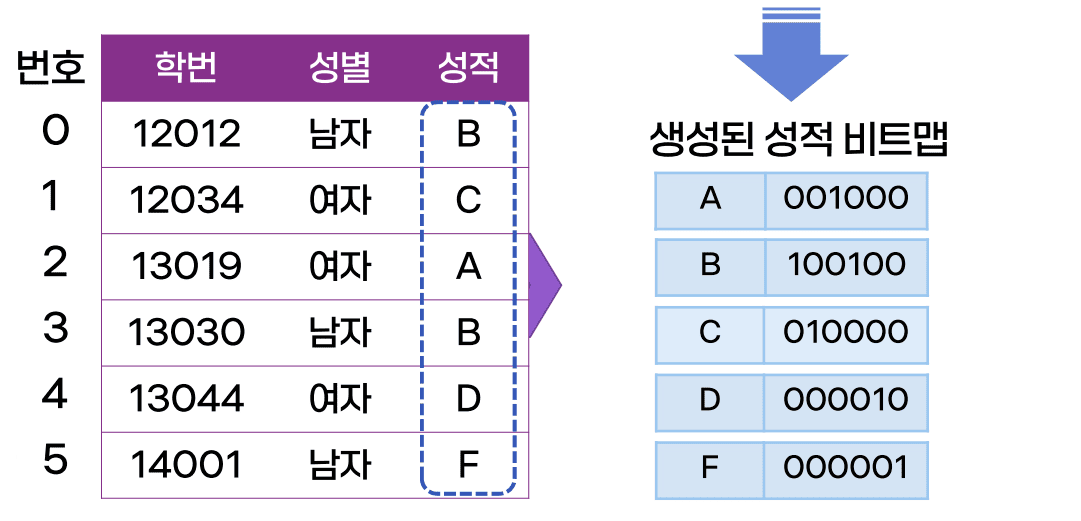
비트맵 인덱스의 사용

• 성별이 남자이고 성적이 B인 학생의 정보를 출력

    SELECT * FROM 학생
    	WHERE 성별 = '남자' AND 성적 = 'B'
  

• 성별의 ‘남자’와 성적의 ‘B’의 비트 열에 대한 비트 논리 곱 연산을 수행

  

  

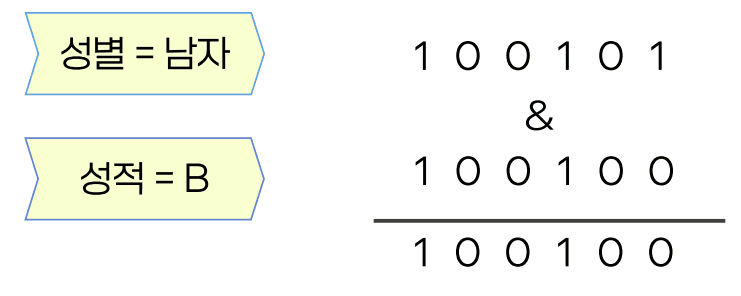
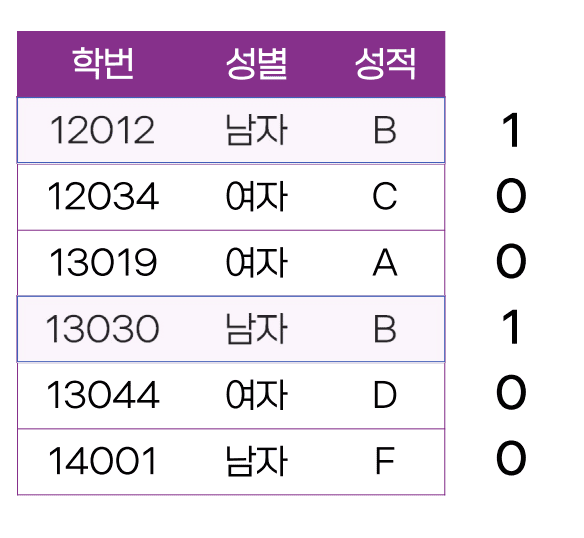
비트맵 인덱스의 사용

• 비트 맵의 활용
  • 컬럼에 대한 값의 범위가 유한하고 비교적 개수가 적은 규모일 때 용이
    • 조건이 맞는 레코드를 빠르게 찾을 수 잇음
  • 적용
    • 직책, 학과, 혈액형 등
• 비트맵 인덱스의 크기
  • 레코드의 크기가 수백 바이트 이상이 되어도 비트 맵 인덱스에서는 하나의 비트로 표시
  • 실제 릴레이션 크기에 비해 매우 작은 것이 장점
• 기본 키 또는 UNIQUE가 설정 된 키에 비트맵 인덱스를 적용할 경우, 인덱스의 크기가 굉장히 커질 수도

연습 문제

---

1. 다음 해시 인덱스 구조에서 탐색 키를 버킷 주소에 대응 시키는 h를 무엇이라고 하는가?

   

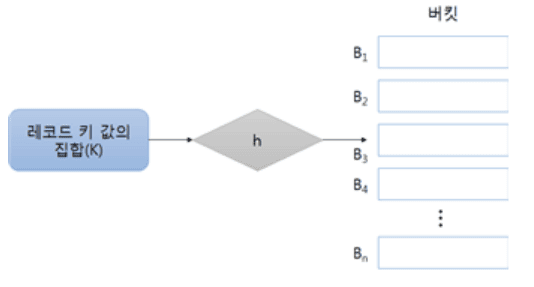
   a. 해시 함수

   • 해싱 기법이란 탐색 키를 특정 버킷에 대응 시켜 레코드를 그룹화 함으로서 특정 탐색 키를 검색하는 조건에 대해 대응되는 버킷만 검색하여 속도를 높이는 기법을 말함
   • 이 때 각각의 탐색 키를 특정 버킷에 대응 시키는 역할은 해시 함수가 수행함

2. 데이터베이스의 크기에 따라 버킷의 개수가 조절되는 형태의 해싱을 무엇이라고 하는가? a. 동적 해싱

   • 해시 기법은 크게 정적 해싱과 동적 해싱으로 구분 됨
   • 정적 해싱은 버킷의 개수가 데이터베이스의 크기와 관계없이 고정되어 있는 해싱을 기법을 말함
   • 동적 해싱은 공간 낭비를 최소화 하기 위해 데이터베이스 크기에 따라 버킷의 개수가 유동적으로 변하는 해싱 기법을 말함

3. 다음과 같은 테이블에 대해 성별 컬럼에 비트맵 인덱스를 생성했을 때, ‘남자’에 대한 비트 열로 올바른 것은?

   학번	성별	학과
   20120451	남자	컴퓨터과학
   20135132	남자	국어국문학
   20132549	남자	컴퓨터과학
   20145942	여자	행정학
   20145315	남자	경제학
   20156857	여자	컴퓨터과학
   20153546	여자	경제학

   a. 1110100

   • 비트 맵 인덱스는 컬럼 값의 종류가 극히 적은 컬럼에 생성할 수 있는 특수한 형태의 인덱스로, 특정 컬럼 값 v에 대해 비트 열은 각각의 첫 번째 레코드부터 레코드의 컬럼 값이 v일 경우 1, v가 아닐 경우 0으로 연결하여 생성함
   • 따라서 성별 컬럼에서 첫 번째, 두 번째, 세 번째, 다섯 번째 레코드의 성별 컬럼 값이 ‘남자’이므로 ‘남자’에 대한 비트 열은 1110100으로 생성 됨

정리 하기

---

• 해싱은 수학적 함수 개념을 사용한 데이터 관리 기법으로 버킷의 개수가 정해진 정적 해싱과 데이터베이스의 크기에 따라 버킷의 개수가 변경되는 동적 해싱으로 구분됨
• 해시 함수는 레코드의 탐색 키 값과 저장되어야 하는 버킷의 주소를 대응 시키는 역할을 수행하며, 레코드가 버킷에 균등하게 배분 되는 해시 함수가 가장 이상적임
• 충돌 발생으로 서로 다른 탐색 키가 동일한 버킷에 대응될 수 있으며 이를 동거자라고 함
• 특정 버킷에 많은 충돌이 발생하여 더 이상의 레코드나 인덱스 엔트리가 저장될 수 없을 때 이를 오버플로라 함
• 확장성 해싱은 데이터베이스의 크기에 따라 버킷이 확장되는 동적 해싱 기법의 일종으로 디렉토리와 버킷으로 구성되며 디렉토리의 주소와 버킷의 주소로 구성되는 모조 키를 사용함
• 비트맵 인덱스는 다중 키를 가진 질의를 보다 효율적으로 처리하기 위해 고안된 인덱스임
  • 비트맵은 간단한 비트 배열로 이루어져 있음
• 비트맵 인덱스를 사용하여 레코드를 검색 시 주어진 각각의 조건에 해당하는 비트 열을 비트 AND 연산을 수행하여 최종적으로 생성되는 비트열로 조건을 만족하는 레코드의 위치를 빠르게 파악할 수 있음

체크 포인트

---

1. 다음은 인덱스에 관한 내용이다. (가)와 (나)가 설명하는 용어를 순서대로 나열한 것은?

    (가)는 많은 수의 행을 가진 릴레이션을 위해 사용하는 기법으로, 하나 이상의 열에 대해 인덱스를 생성하며 적은 수의 유일한 값들을 갖는 열들에 적합하다.
    (나)는 디렉터리(directory)와 버킷(bucket) 집합을 사용하는 기법으로, 데이터베이스가 증가하고 축소되는 변화에 유연하다.
   

   a. 비트맵 인덱스, 확장성 해싱

2. 다음 ‘학생성적’ 릴레이션과 각 투플의 번호를 참고하여 ‘성적’ 속성에 대한 비트맵 인덱스를 적절히 표현한 것은?

   

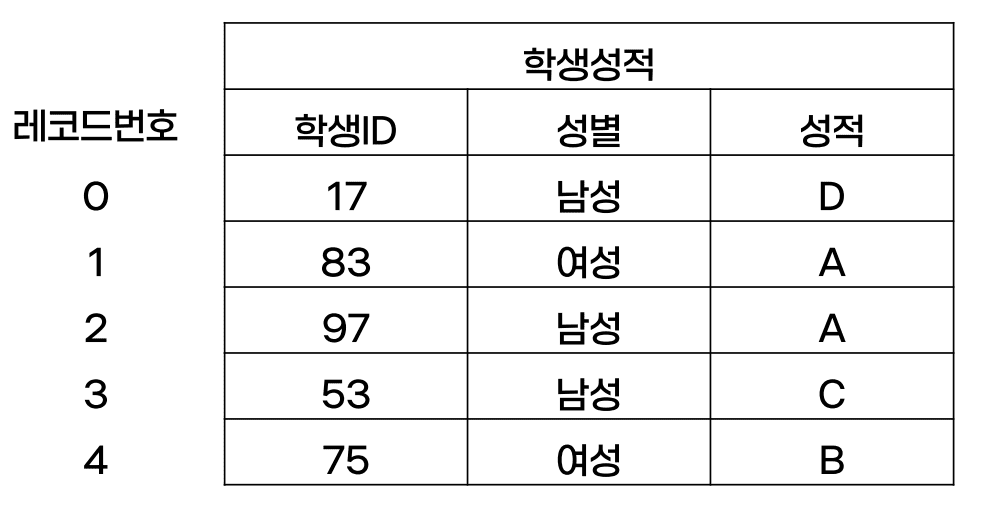
   a.