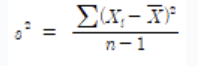💡해당 게시글은 방송통신대학교 김성수, 이기재 교수님의 '데이터 정보 처리 입문' 강의를 개인 공부 목적으로 메모하였습니다.

학습 개요

데이터의 특성을 요약할 때 기본적으로 이용되는 기술통계량과 그래프들을 알아보고, 웹을 활용한 데이터분석 예를 알아봄

학습 목표

기술 통계량을 이해할 수 있음
연속인 자료에 이용되는 통계 그래프를 설명할 수 있음
웹을 활용하여 기술 통계량을 구하고, 통계 그래프를 그려볼 수 있음

강의록

연속형 자료의 정리

중심 측도: 평균

중심 위치의 측도
- 평균, 중앙 값, 최빈 값 등이 있으며, 가장 많이 사용되는 것은 평균(mean)임
평균 정의
- 관측한 자료의 값들을 X₁, X₂, … Xₙ이라 할 때, 다음과 같이 정의 됨
- 표본 평균
  1 x̄ = n / X₁ + X₂ + … + Xₙ = n / ΣXᵢ
  - x̄는 엑스 바(bar)라고 읽음
- 평균은 어느 한 자료 값이 다른 값들보다 아주 크거나 작은 특이 값(outlier; 이상치)의 영향을 많이 받음

ex)

자료: 5, 4, 7, 6, 8, 10, 11, 0, 7, 18인 경우
- 평균 x̄
  1 10 / 5 + 4 + … + 7 + 18 = 10 / 76 = 7.6
자료: 5, 4, 7, 6, 8, 10, 11, 0, 7, 18, 100인 경우
- 평균 x̄
  1 11 / 5 + 4 + … + 7 + 18 + 100 = 11 / 176 = 16

R 코드

  
  aval = c(5, 4, 7, 6, 8, 10, 11, 0, 7, 18)
  sum(aval)
  mean(aval)
  [1] 7.6

중심 측도: 절사 평균

절사 평균(trimmed mean)
- 표본에서 가장 작은 값 일부와 가장 큰 값 일부를 제외하고 계산된 평균
- 10% 절사 평균은 표본에서 가장 작은 값 10%와 가장 큰 값 10%를 제외하고 계산된 평균을 말함
- 절사 평균은 특이치(outlier)의 영향을 덜 받는 효과

ex)

자료: 5, 4, 7, 6, 8, 10, 11, 0, 7, 18 인 경우
자료를 크기 순 정렬: 0, 4, 5, 6, 7, 7, 8, 10, 11, 18
- 10% 절사 평균
  - x̄ .₁₀ = 8 / 4 + 5 + 6 + 7 + 7 + 8 + 10 + 11 = 7.25
- 20% 절사 평균
  - x̄ .₂₀ = 6 / 5 + 6 + 7 + 7 + 8 + 10 = 7.1667

R 코드

  
  aval = c(5, 4, 7, 6, 8, 10, 11, 0, 7, 18)
  mean(aval)
  [1] 7.6
  mean(aval, trim = 0.10) # 양 끝 10%씩 제외
  [1] 7.25
  mean(aval, trim = 0.20) # 양 끝 20%씩 제외
  [1] 7.166667
  median(aval) # 중앙 값
  [1] 7

중심 측도: 중앙 값

중앙 값(median)
- 자료를 크기 순서로 나열했을 때 중앙에 놓이는 값
자료의 수를 n이라 할 때, (n + 1)/2 번째의 값을 중앙 값으로 함
- n이 홀수
  - (n + 1) / 2 번째 값
- n이 짝수
  - (n / 2)번째 값과 (n / 2 + 1)번째 값의 평균
ex)
- 자료: 5, 4, 7, 6, 8, 10, 11, 0, 7, 12, 13, 18, 14 인 경우 (n=13)
  - 크기 순 정렬: 0, 4, 5, 6, 7, 7, 8, 10, 11, 12, 13, 14, 18
  - 중앙 값 위치: (13 + 1) / 2 = 7, 7번째 값 = 8
- 자료: 5, 4, 7, 6, 8, 10, 11, 0, 7, 12, 13, 18, 14, 20 인 경우 (n=14)
  - 크기 순 정렬: 0, 4, 5, 6, 7, 7, 8, 10, 11, 12, 13, 14, 18, 20
  - 중앙 값 위치: (14 + 1) / 2 = 7.5 = 7번째와 8번째 값의 평균 값 (8 + 10) / 2 = 9
- 자료: 5, 4, 7, 6, 8, 10, 11, 0, 9, 14 (n=10), 평균=7.4
  - 자료 순서 : 0, 4, 5, 6, 7, 8, 9, 10, 11, 14
  - 중앙 값 : (10 + 1) / 2 = 5.5번째 = 5번째와 6번째 값의 평균 = (7 + 8) / 2 = 7.5
- 자료: 5, 4, 7, 6, 8, 10, 11, 0, 9, 14, 100 (n=11), 평균=15.82
  - 자료 순서 : 0, 4, 5, 6, 7, 8, 9, 10, 11, 14, 100
  - 중앙 값 : (11 + 1) / 2 = 6번째 값 = 8
- R 코드
  1 2 aval = c(5, 4, 7, 6, 8, 10, 11, 0, 9, 14, 100) median(aval)

중심 측도: 최빈 값(mode)

최빈 값
- 자료 중 가장 빈도가 많은 값
이산형 자료일 경우 도수 분포 표만 살펴보면 쉽게 구할 수 있음
연속형 자료일 경우 자료를 몇 개의 계급 구간으로 나누어 가장 도수가 높은 계급의 중간 값을 최빈값으로 정하기도 함
- ex)
  - 자료: 13, 18, 13, 16, 14, 21, 13 : mode = 13

산포도 측도

산포도의 측도(measure of dispersion)
- 자료가 흩어진 정도를 수치로 측정하는 것
대표적인 산포도의 측도
- 분산 및 표준 편차
- 이외에도 변동 계수, 범위, 사분위수 범위 등이 이용됨

산포도 측도: 분산, 표준 편차

분산(variance)
- 각 자료 값과 평균과의 거리를 제곱하여 합한 후 이를 자료의 수로 나눈 측도
- 표본 분산
  1 s² = n -1 / Σ(xᵢ + x̄)²
- 자료가 평균에서 많이 흩어져 있으면 분산이 커지고, 평균 주위에 몰려 있으면 분산이 작게 됨
표준 편차(standard deviation)
- 분산의 제곱근
- 표본 표준 편차
  1 s = √s²

산포도 측도: 변동 계수, 범위

변동 계수(coefficient of variation):
1 CV = x̄ / s * 100
- 자료의 개수나 측정 단위가 다른 두 개 이상의 자료에 대한 표준 편차를 비교하는 것은 무의미함
- 이러한 경우에 사용하는 측도가 표준 편차를 평균으로 나눈 표준화 된 표준 편차인 변동 계수(coefficient of variation)를 사용
- 변이 계수라고도 함
범위(Range)
- 최대 값 – 최소 값
- 범위는 계산하기가 간편 하나 극 단점이 있을 경우 올바른 산포의 측도가 되지 못함

산포도 측도: 사분위수 범위

p% 백분위수(percentile)
- 자료를 작은 값부터 큰 값까지 순서대로 늘어놓았을 때 p% 번째 자료를 말함
- 제 1 사분위수 (1st quartile, Q₁ 으로 표시): 백분위 수 중 25% 백분위수
- 제 2 사분위수 (2nd quartile, Q₂ 으로 표시, 중앙 값): 백분위 수 중 50% 백분위수
- 제 3 사분위수 (3rd quartile, Q₃ 으로 표시): 백분위 수 중 75% 백분위수
사분위수 범위(IQR; Interquartile Range)
- 제 3 사분위수와 제 1 사분위수의 차이
  1 IQR = Q₃ - Q₁
  - 중앙 값을 중심으로 50%의 자료가 포함되는 범위이며, 특이 값의 영향을 덜 받음

산포도 측도

R을 이용한 계산

  
  aval = c(5, 4, 7, 6, 8, 10, 11, 0, 7, 18)
    
  # 표준 편차
  sd(aval)
  # 4.788876
    
  # 사분위수 범위 (IQR)
  IQR(aval)
  # 4.25 # Q3(9.50) - Q1(5.25) = 4.25
    
  # 요약 통계량 (최소값, Q1, 중앙값, 평균, Q3, 최대값)
  summary(aval)
  # Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
  # 0.00    5.25    7.00    7.60    9.50   18.00
    
  # 특정 백분위수 계산 (Q1, Q2, Q3)
  quantile(aval, probs = c(0.25, 0.5, 0.75))
  # 25%  50%  75%
  # 5.25 7.00 9.50

연속형 자료의 그래프

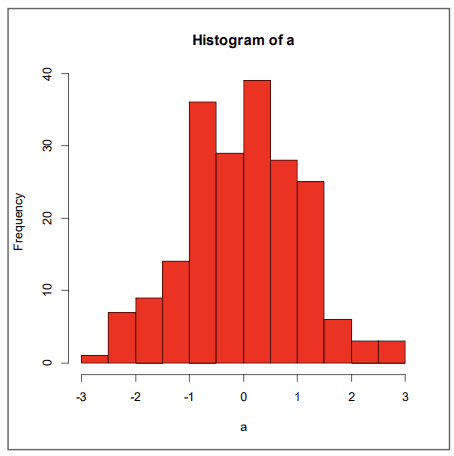
연속형 자료의 그래프: 히스토그램 (Histogram)

히스토그램 (Histogram)
- 연속인 자료를 일정한 계급으로 나누어 각 계급에 속한 도수들을 정리한 도수 분포 표를 이용하는 작성한 그래프
- 히스토그램은 연속인 자료의 분포를 살펴볼 때 이용되는 그래프로서 많은 양의 자료에 적합
  - 대칭성, 집중도 등

R을 이용한 계산

  
  # 정규분포 따르는 난수 200개 생성
  a = rnorm(200)
  # 히스토그램 그리기 (빨간색으로)
  hist(a, col="RED")

연속형 자료의 그래프: 줄기-잎 그림 (Stem-and-Leaf Plot)

줄기-잎 그림 (Stem-and-Leaf Plot)
- 분포의 대략적인 형태를 살펴보기 위하여 작성되는 그래프로 군집의 존재 여부, 집중도가 높은 구간, 대칭성의 여부, 자료의 범위 및 산포, 특이 값의 존재 여부 등을 파악하는데 이용됨
  - 원자료의 정보를 유지하면서 분포를 보여줌
- 자료의 값을 ‘줄기(stem)’와 ‘잎(leaf)’으로 나누어 표현하는 그래프
- 보통 큰 자릿수를 줄기로, 마지막 자릿수를 잎으로 사용

ex) 점수 자료

  54 57 55 23 51 64 90 51 52 43 15 10 82 74 54 78 37 73 52 48 41 33 52 30 41 51 18 39 46 28 53 44 46 56 28 58 29 58 67 35 25 38 61 53 23 73 69 47 41 45 77 56 89 28 54 99 10 43 35 24 21 23 67 14 53

  
  # "c:/data/dataintro/score.txt" 경로에서 데이터를 읽어옴
  score = scan("c:/data/dataintro/score.txt")
  stem(score)
    
  # The decimal point is 1 digit(s) to the right of the |
    
  # 1 | 00458        # 10, 10, 14, 15, 18
  # 2 | 1333458889   # 21, 23, 23, 23, 24, 25, 28, 28, 28, 29
  # 3 | 0355789      # 30, 33, 35, 35, 37, 38, 39
  # 4 | 11133456678  # 41, 41, 41, 43, 43, 44, 45, 46, 46, 47, 48
  # 5 | 111222333444566788 # 51, 51, 51, 52, 52, 52, 53, 53, 53, 54, 54, 54, 55, 56, 56, 57, 58, 58
  # 6 | 14779        # 61, 64, 67, 67, 69
  # 7 | 33478        # 73, 73, 74, 77, 78
  # 8 | 29           # 82, 89
  # 9 | 09           # 90, 99

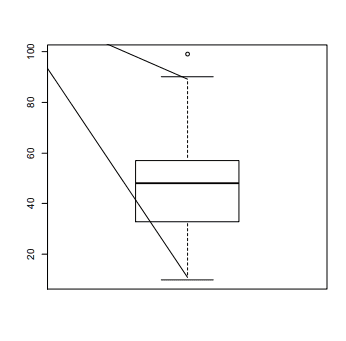
연속형 자료의 그래프: 상자 그림 (Box Plot)

다섯 숫자 요약 (Five-number summary)
- 자료의 분포를 요약하는 5가지 값
  - 최소 값, 제 1 사분위수( Q₁), 중앙값, 제 3 사분위수(Q₃), 최대 값
상자 그림 (Box Plot)
- 다섯 숫자 요약을 특이 값과 함께 그래프로 표현한 것으로서 분포의 상태, 특이 값의 유무, 여러 집단의 수치 자료를 비교하고자 할 때 유용하게 이용됨
상자 그림 그리는 방법
1. 다섯 숫자 요약을 구함
2. 제 1 사분위수, 제 3 사분위수에 해당하는 수직선 상의 위치에 네모 상자의 양 끝이 오게 하고 상자 내의 중앙 값에 해당되는 위치에 가로지르는 막대 표시를 함
3. 안울타리(inner fence)값을 구함
  1 IFₗ = Q₁ - 1.5 * IQR
  1 IFᵤ = SQ₃ - 1.5 * IQR
  - 단, IQR = Q₃ - Q₁
4. 안울타리의 안쪽에 있으면서 경계에 가장 가까운 인접 값(adjacent value, AV)를 찾아 상자의 양 끝을 연결 함
5. 안울타리 바깥에 있는 자료 점을 특이 값으로 간주하고 “o” 또는 “*” 표시를 함

  
  score = scan("c:/data/dataintro/score.txt")
  # 줄기-잎 그림 (참고용)
  stem(score)
  # The decimal point is 1 digit(s) to the right of the |
  # 1 | 00458
  # 2 | 1333458889
  # 3 | 0355789
  # 4 | 11133456678
  # 5 | 111222333444566788
  # 6 | 14779
  # 7 | 33478
  # 8 | 29
  # 9 | 09
    
  # 요약 통계량
  summary(score)
  # Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
  # 10.00   33.00   48.00   47.45   57.00   99.00
    
  # 상자 그림 그리기
  boxplot(score)

웹 데이터 분석

웹의 활성화
웹을 이용한 데이터 분석 방법의 발전
- 통계 교육 효과 증대
- 그래프를 이용한 데이터의 이해 효과
- Free

StatPages.net

StatPages.net
데이터 분석, 통계적 방법, 전자 교재, 통계 강의 등 다양한 내용
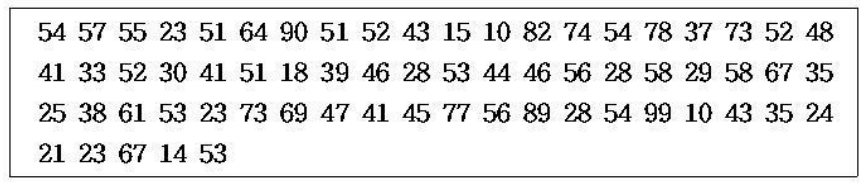
ex) StatPages.net의 “Interactive Stats”을 이용하여 다음 점수 자료의 히스토그램을 그리고, 기술 통계량을 구해보자.
1. 히스토그램 그리기
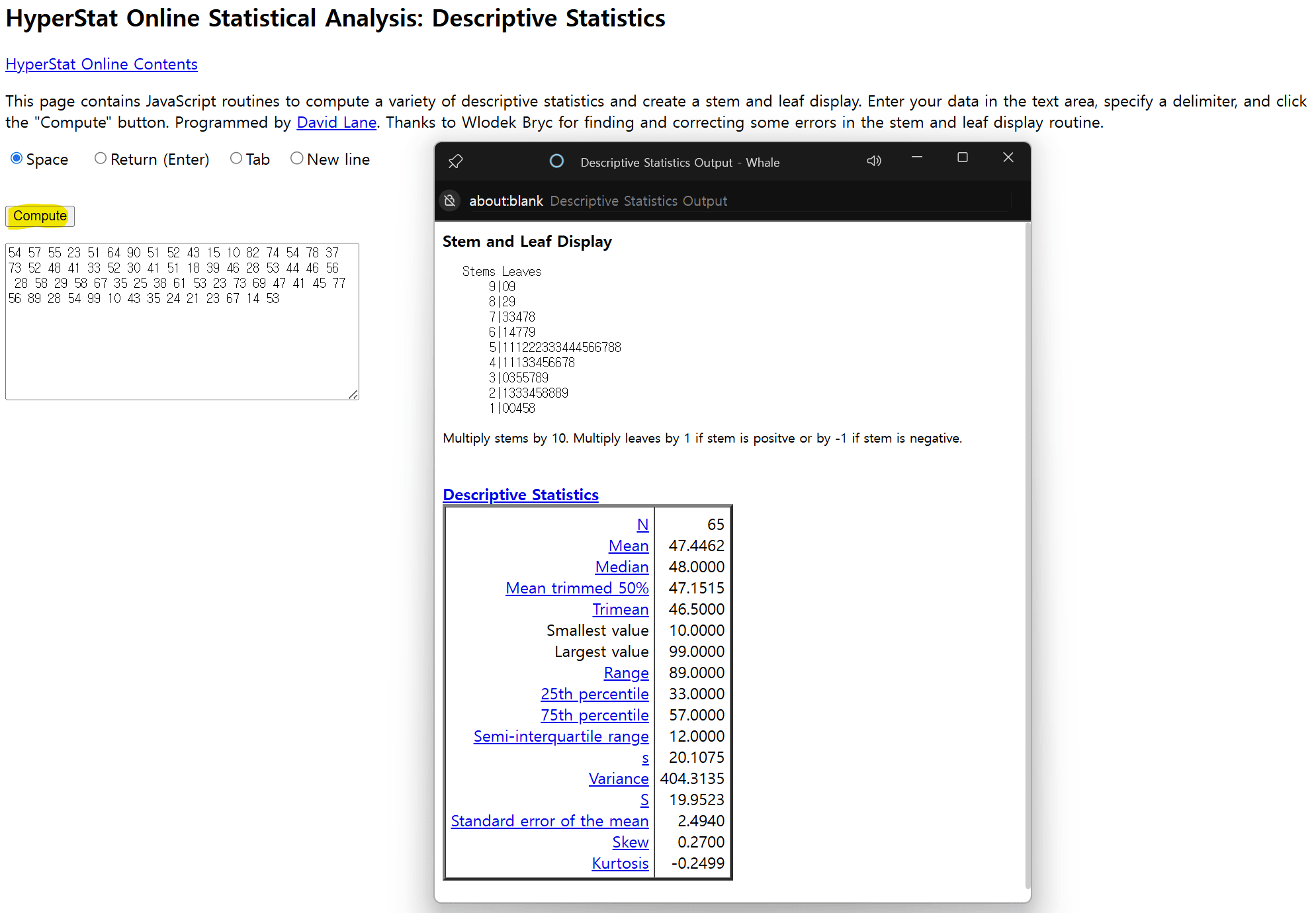
2. 줄기-잎 그림 및 기술통계량 구하기

Interactivate

Interactivate
확률, 통계, 그래프 등을 대화형으로 제공해주는 사이트
히스토그램, 파이 차트, 산점도, 줄기-잎 그림 등의 다양한 통계 그래프
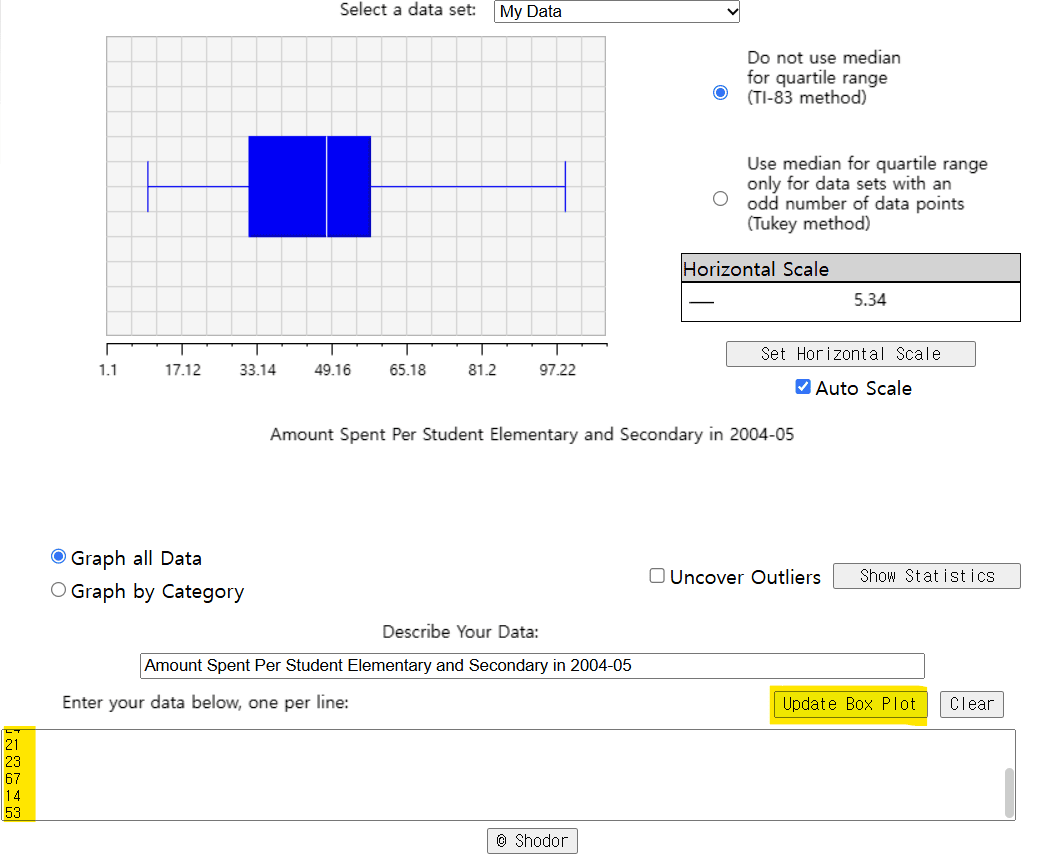
ex) 상자 그림 그리기

eStat

eStat
초,중,고,대 교육용 통계 패키지 (크롬에 최적화)
교육 현장에서 통계 분석 및 시각화를 쉽게 수행할 수 있도록 다양한 기능을 제공

연습 문제

다음 중 표본 평균을 구하는 공식은?
a.
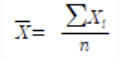
자료의 개수나 측정 단위가 다른 두 개 이상의 자료에 대한 표본 집단 간의 상대적인 산포를 비교할 때 이용되는 측도로, 두 집단의 단위가 다르거나, 단위는 같지만 평균의 차이가 클 때 두 그룹의 산포를 비교하는 데 유용하게 이용되는 측도는?
a. 변동 계수
탐색적 자료 분석의 관점에서 살펴볼 때 한 묶음의 자료를 정리하는 숫자로서 다섯 숫자 요약이란 다음 중 무엇인가?
a. 최소값, 최대값, 중앙값, 제 1 사분위수, 제 3 사분위수

조사된 자료가 다음과 같다. 중앙값은?

    
 22  5  21  16  18  20  23  24  32  490  36

a. 22

다음 중 표본 분산을 구하는 공식은?
a.

[데이터 정보 처리 입문] 4강 - 통계 정보의 검색 및 활용 2

학습 개요

학습 목표

강의록

연속형 자료의 정리

중심 측도: 평균

중심 측도: 절사 평균

중심 측도: 중앙 값

중심 측도: 최빈 값(mode)

산포도 측도

산포도 측도: 분산, 표준 편차

산포도 측도: 변동 계수, 범위

산포도 측도: 사분위수 범위

산포도 측도

연속형 자료의 그래프

연속형 자료의 그래프: 히스토그램 (Histogram)

연속형 자료의 그래프: 줄기-잎 그림 (Stem-and-Leaf Plot)

연속형 자료의 그래프: 상자 그림 (Box Plot)

웹 데이터 분석

웹 데이터 분석

StatPages.net

Interactivate

eStat

연습 문제

Further Reading

[데이터 정보 처리 입문] 2강 - 데이터 입력과 점검

[데이터 정보 처리 입문] 3강 - 통계 정보의 검색 및 활용

[데이터 정보 처리 입문] 5강 - 문서 작성