개요
- 비교하지 않는 정렬은 데이터의 특성을 활용하여 직접 위치를 결정하는 알고리즘임
- 비교 연산 없이 정렬하므로 특정 조건에서 $O(n)$까지 가능함
- 정수 데이터나 제한된 범위의 데이터에 특화되어 있음
비교하지 않는 정렬
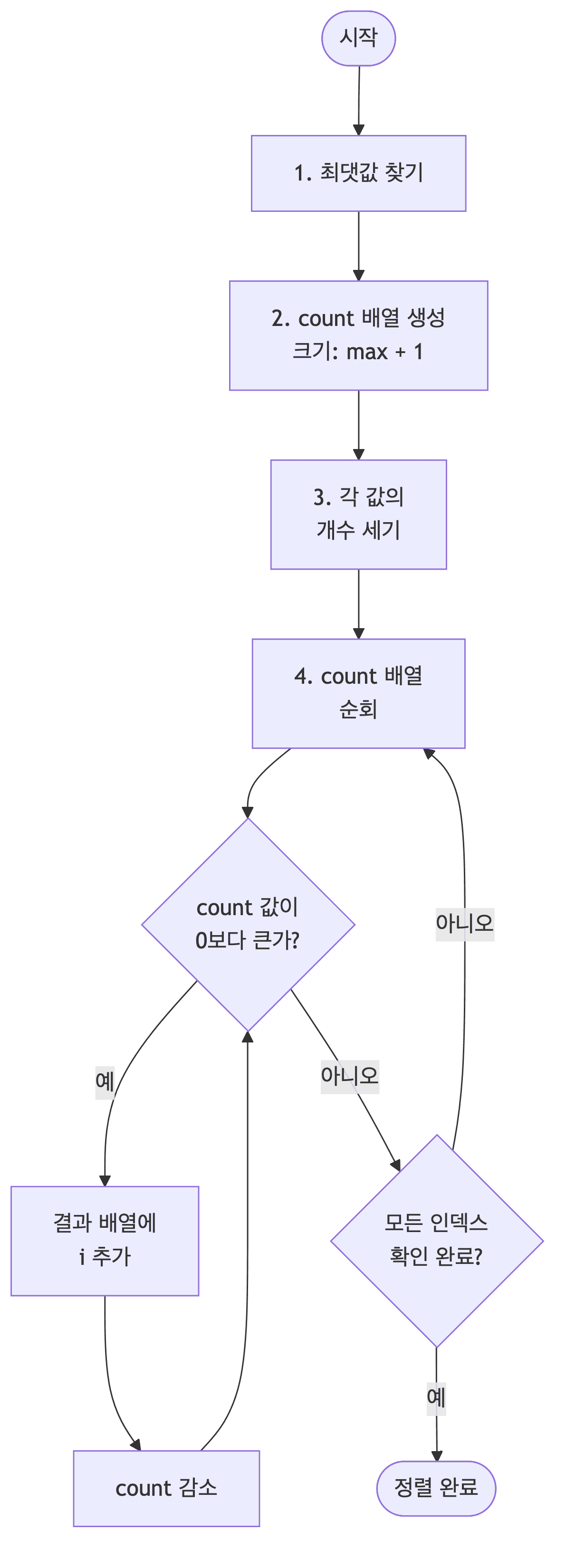
계수 정렬
- 데이터의 크기 범위가 정해져 있을 때, 각 값이 몇 개씩 있는지 세어 정렬함
- 비교 연산 없이 인덱스를 활용하여 정렬함
-
정수 데이터에 특화된 정렬 알고리즘임
- 시간 복잡도
- 모든 경우
- $O(n + k)$ (k는 최댓값)
- 모든 경우
- 공간 복잡도
- $O(k)$
-
안정성
- 안정적임
- 특징
- 시간 복잡도가 매우 낮음
- 음수나 매우 큰 범위의 숫자에는 부적합함
- 안정성을 보장하기 위해 입력 배열을 뒤에서부터 순회하여 결과 배열에 채움
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void countingSort(int[] array) {
if (array.length == 0) return;
int max = array[0];
for (int num : array) {
if (num > max) max = num;
}
int[] count = new int[max + 1];
for (int num : array) {
count[num]++;
}
int idx = 0;
for (int i = 0; i <= max; i++) {
while (count[i] > 0) {
array[idx++] = i;
count[i]--;
}
}
}
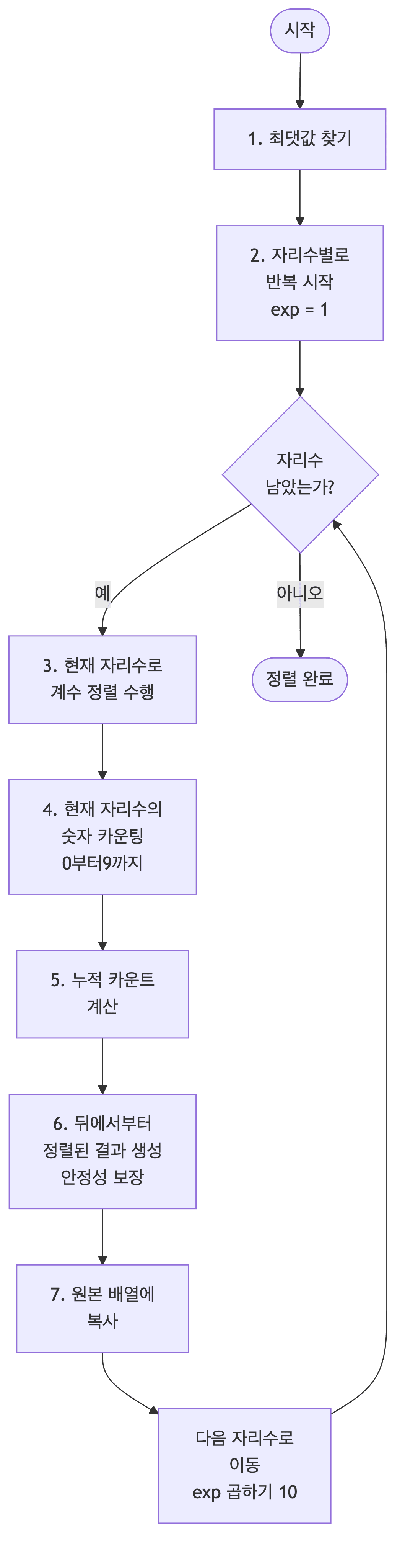
기수 정렬
- 낮은 자리수부터 높은 자리수까지 차례로 정렬함
- 각 자리수마다 안정한 정렬을 사용함
-
정수의 자리수를 기준으로 분류하여 정렬함
- 시간 복잡도
- 모든 경우
- $O(d \times n)$ (d는 자리수)
- 모든 경우
- 공간 복잡도
- $O(n + k)$
-
안정성
- 안정적임
- 특징
- 정수 정렬에서 매우 빠름
- 추가 메모리가 필요함
- 자리수가 고정되어 있을 때 효율적임
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
void radixSort(int[] array) {
if (array.length == 0) return;
int max = array[0];
for (int num : array) {
if (num > max) max = num;
}
for (int exp = 1; max / exp > 0; exp *= 10) {
countingSortByDigit(array, exp);
}
}
void countingSortByDigit(int[] array, int exp) {
int n = array.length;
int[] output = new int[n];
int[] count = new int[10];
for (int i = 0; i < n; i++) {
count[(array[i] / exp) % 10]++;
}
for (int i = 1; i < 10; i++) {
count[i] += count[i - 1];
}
for (int i = n - 1; i >= 0; i--) {
int digit = (array[i] / exp) % 10;
output[count[digit] - 1] = array[i];
count[digit]--;
}
System.arraycopy(output, 0, array, 0, n);
}
알고리즘 선택 가이드
데이터 크기에 따른 선택
-
작은 데이터셋 (n < 50)
- 삽입 정렬이 효율적임
- 구현이 단순하고 오버헤드가 적음
-
중간 크기 데이터셋
- 퀵 정렬이 일반적으로 가장 빠름
- 대부분의 표준 라이브러리에서 사용됨
-
대규모 데이터셋
- 병합 정렬이나 힙 정렬로 안정적인 성능 보장
- 최악의 경우에도 $O(n \log n)$ 보장
데이터 특성에 따른 선택
-
거의 정렬된 데이터
- 삽입 정렬이나 버블 정렬의 최적화 버전이 좋음
- $O(n)$에 가까운 성능을 낼 수 있음
-
역순으로 정렬된 데이터
- 퀵 정렬은 피하고 병합 정렬 사용
- 최악의 경우를 피할 수 있음
-
중복이 많은 데이터
- 3-way 퀵 정렬이나 계수 정렬 고려
- 중복 데이터 처리에 최적화됨
요구사항에 따른 선택
-
일반적인 경우
- 퀵 정렬
- 대부분의 프로그래밍 언어의 표준 라이브러리가 퀵 정렬 기반임
-
최악의 경우 보장 필요
- 병합 정렬이나 힙 정렬
- 항상 $O(n \log n)$을 보장함
-
안정한 정렬 필요
- 병합 정렬이나 삽입 정렬
- 동일한 값의 상대적 순서 유지
-
메모리 제약이 심할 때
- 힙 정렬
- 제자리 정렬로 추가 메모리 불필요
-
정수 범위가 제한적
- 계수 정렬이나 기수 정렬
- $O(n)$ 성능 달성 가능
안정성
안정성의 의미
- 안정성이란 동일한 값을 가진 요소들이 정렬 후에도 정렬 전의 상대적 순서를 유지하는 특성임
- 여러 학생의 성적을 이름으로 정렬할 때 같은 성적을 받은 학생들은 원래 순서대로 유지되어야 한다면 안정한 정렬이 필요함
안정성이 중요한 경우
-
여러 기준으로 순차적으로 정렬할 때
- 먼저 정렬한 기준의 순서를 유지해야 함
-
데이터의 원래 순서가 의미를 가질 때
- 입력 순서가 중요한 정보일 경우
-
정렬 전 인덱스 정보를 보존해야 할 때
- 원본 데이터의 위치 정보가 필요한 경우
안정성 분류
-
안정한 정렬
- 버블 정렬
- 삽입 정렬
- 병합 정렬
- 계수 정렬
- 기수 정렬
-
불안정한 정렬
- 선택 정렬
- 퀵 정렬
- 힙 정렬
정리
- 비교하지 않는 정렬은 특정 조건에서 $O(n)$까지 가능함
- 계수 정렬은 정수 범위가 제한적일 때 매우 효율적임
- 기수 정렬은 자리수가 고정된 정수 데이터에 적합함
- 데이터 크기, 특성, 요구사항을 종합적으로 고려하여 알고리즘을 선택해야 함
- 안정성은 여러 기준으로 정렬하거나 원래 순서가 중요할 때 필수적임
- 작은 데이터는 삽입 정렬, 일반적인 경우는 퀵 정렬, 최악 보장이 필요하면 병합이나 힙 정렬을 사용함
- 정수 데이터로 범위가 제한적이면 계수 정렬이나 기수 정렬로 최고의 성능을 얻을 수 있음