- 소수(Prime Number)를 찾는 문제는 고대부터 현대 암호학까지 이어지는 컴퓨터 과학의 핵심 주제임
- 기원전 3세기 그리스 수학자 에라토스테네스(Eratosthenes)가 고안한 에라토스테네스의 체는 2000년이 지난 지금도 특정 범위 내 모든 소수를 찾는 가장 효율적인 알고리즘 중 하나로 평가받고 있음
- 소수를 직접 찾는 것이 아니라 소수가 아닌 수(합성수, Composite Number)를 제거하는 방식으로 동작함
문제 식별 방법
에라토스테네스의 체가 적합한 경우
- 특정 범위 내의 모든 소수를 찾아야 하는 상황
- 범위가 $10^6 \sim 10^8$ 정도로 크지만 메모리가 충분한 경우
- 소수 판별을 여러 번 반복해야 하여 전처리가 효율적인 상황
- 소수의 개수를 세거나 범위 내 소수 목록이 필요한 경우
다른 알고리즘을 고려해야 하는 경우
- 단일 숫자의 소수 여부만 확인할 때
- Trial Division ($O(\sqrt{n})$)이 더 효율적
- 범위가 $10^9$ 이상으로 매우 큰 경우
- 세그먼티드 시브 사용 필요
- $10^{18}$ 이상의 매우 큰 단일 소수 판별
- 밀러-라빈 알고리즘 사용 권장
핵심 개념과 동작 원리
왜 “체(Sieve)”인가
- 에라토스테네스의 체는 소수를 직접 찾는 것이 아니라 소수가 아닌 수를 제거하는 방식으로 동작함
- 마치 체로 걸러내듯이 소수가 아닌 수들을 걸러내기 때문에 체(Sieve)라는 이름이 붙었음
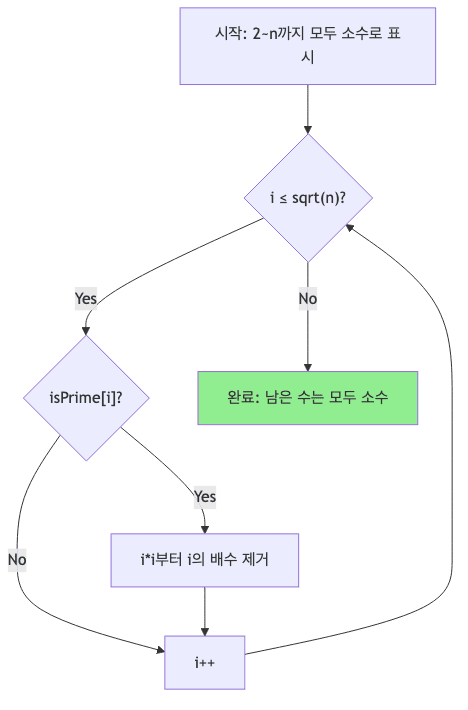
단계별 동작 과정
-
30 이하의 소수 찾기
-
1단계 - 초기화
1 2
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
-
2단계 - 2의 배수 제거
1 2
2 3 X 5 X 7 X 9 X 11 X 13 X 15 X 17 X 19 X 21 X 23 X 25 X 27 X 29 X
-
3단계 - 3의 배수 제거
1 2
2 3 X 5 X 7 X X X 11 X 13 X X X 17 X 19 X X X 23 X 25 X X X 29 X
-
4단계 - 5의 배수 제거
1 2
2 3 X X X 7 X X X 11 X 13 X X X 17 X 19 X X X 23 X X X X X 29 X
- $\sqrt{30} \approx 5.5$이므로 여기서 멈춤
-
최종 결과
- 2, 3, 5, 7, 11, 13, 17, 19, 23, 29
왜 $\sqrt{n}$까지만 확인하는가
- n의 약수는 항상 쌍으로 존재함
- 예를 들어 36의 약수를 보면
- $1 \times 36 = 36$
- $2 \times 18 = 36$
- $3 \times 12 = 36$
- $6 \times 6 = 36$ (← $\sqrt{36}$)
- 이후는 순서만 바뀜 ($12 \times 3$, $18 \times 2$, $36 \times 1$)
- 즉 한 쪽이 $\sqrt{n}$보다 크면 다른 쪽은 반드시 $\sqrt{n}$보다 작음
- 따라서 $\sqrt{n}$까지만 확인하면 모든 합성수를 걸러낼 수 있음
시간 복잡도 분석
복잡도: $O(n \log \log n)$
- 에라토스테네스의 체의 시간 복잡도는 $O(n \log \log n)$으로 거의 선형 시간에 가까운 성능을 보임
복잡도 유도
- 내부 루프는 각 소수
p에 대해n/p번 실행됨
- 소수의 역수의 합(Prime Harmonic Series)은 $\log(\log n)$에 근사하므로 $O(n \times \log(\log n))$
성능 비교
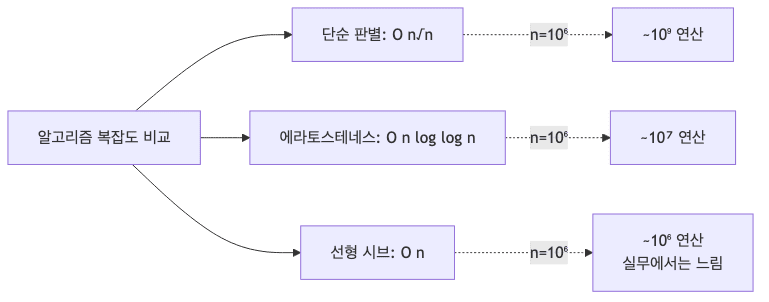
-
실제 성능
- $n = 10^6$ (약 10ms)
- $n = 10^7$ (약 100ms)
- $n = 10^8$ (약 1.2초)
Java 기본 구현
표준 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
import java.util.Arrays;
public class SieveOfEratosthenes {
/**
* 에라토스테네스의 체를 이용한 소수 판별
* @param n 범위의 상한값
* @return 소수 여부를 담은 boolean 배열
*/
public static boolean[] sieveOfEratosthenes(int n) {
// n+1 크기의 배열 생성 (인덱스와 숫자를 일치시키기 위해)
boolean[] isPrime = new boolean[n + 1];
// 모든 수를 소수로 가정 (true로 초기화)
Arrays.fill(isPrime, true);
// 0과 1은 소수가 아님
isPrime[0] = false;
isPrime[1] = false;
// 2부터 √n까지 반복
for (int i = 2; i * i <= n; i++) {
// i가 소수인 경우에만 배수 제거
if (isPrime[i]) {
// i²부터 시작 (i*k, k<i는 이미 처리됨)
for (int j = i * i; j <= n; j += i) {
isPrime[j] = false;
}
}
}
return isPrime;
}
/**
* 소수 목록 출력
*/
public static void printPrimes(boolean[] isPrime) {
System.out.print("소수: ");
for (int i = 2; i < isPrime.length; i++) {
if (isPrime[i]) {
System.out.print(i + " ");
}
}
System.out.println();
}
public static void main(String[] args) {
int n = 100;
boolean[] primes = sieveOfEratosthenes(n);
printPrimes(primes);
// 특정 숫자의 소수 여부 확인
int num = 17;
System.out.println(num + "은(는) 소수인가? " + primes[num]);
}
}
i * i <= n- $\sqrt{n}$까지만 확인하는 최적화
j = i * ii의 배수 중i²미만은 이미 처리되었으므로i²부터 시작- 예:
i=5일 때5×2=10,5×3=15,5×4=20은 이미 2, 3의 배수로 제거됨
j += ii의 배수를 순차적으로 제거
1
2
소수: 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97
17은(는) 소수인가? true
최적화 기법
짝수 제거
- 2를 제외한 모든 짝수는 합성수임
- 이를 활용하면 메모리를 50% 절감할 수 있음
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
import java.util.Arrays;
public class OptimizedSieve {
/**
* 짝수를 제외한 에라토스테네스의 체
* 메모리 사용량을 절반으로 줄임
*/
public static boolean[] optimizedSieve(int n) {
// 홀수만 저장 (index i는 2*i+1을 나타냄)
int size = (n - 1) / 2;
boolean[] isPrime = new boolean[size + 1];
Arrays.fill(isPrime, true);
// 3부터 시작하여 홀수만 확인 (2는 별도 처리)
for (int i = 3; i * i <= n; i += 2) { // i를 홀수만 증가
if (isPrime[i / 2]) { // i가 소수이면
// i의 홀수 배수만 제거
// i²부터 시작: i×2, i×3, i×4는 이미 처리됨
// 2*i씩 증가: 짝수 배수는 처리할 필요 없음 (이미 합성수)
for (int j = i * i; j <= n; j += 2 * i) {
isPrime[j / 2] = false; // 배열 인덱스 변환 (홀수만 저장)
}
}
}
return isPrime;
}
public static void printOptimizedPrimes(boolean[] isPrime, int n) {
System.out.print("소수: 2 "); // 2는 유일한 짝수 소수
for (int i = 1; i < isPrime.length; i++) {
if (isPrime[i]) {
System.out.print((2 * i + 1) + " ");
}
}
System.out.println();
}
public static void main(String[] args) {
int n = 100;
boolean[] primes = optimizedSieve(n);
printOptimizedPrimes(primes, n);
}
}
- 메모리 50% 절감
- 연산 횟수 약 50% 감소
- 실행 시간 약 30% 개선
BitSet 사용
- Java의
BitSet을 사용하면 메모리를 1/8로 줄일 수 있음
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import java.util.BitSet;
public class BitSetSieve {
/**
* BitSet을 사용한 메모리 효율적인 구현
* boolean 배열 대비 약 1/8의 메모리만 사용
*/
public static BitSet bitSetSieve(int n) {
BitSet isPrime = new BitSet(n + 1);
// BitSet은 기본값이 false이므로 소수를 true로 설정
isPrime.set(2, n + 1); // 2부터 n까지 true로 설정
isPrime.clear(0);
isPrime.clear(1);
for (int i = 2; i * i <= n; i++) {
if (isPrime.get(i)) { // i번째 비트가 true(소수)이면
// i의 배수를 모두 false로 설정
for (int j = i * i; j <= n; j += i) {
isPrime.clear(j); // j번째 비트를 false로 변경
}
}
}
return isPrime;
}
public static void main(String[] args) {
int n = 100;
BitSet primes = bitSetSieve(n);
System.out.print("소수: ");
for (int i = primes.nextSetBit(0); i >= 0; i = primes.nextSetBit(i + 1)) {
System.out.print(i + " ");
}
System.out.println();
System.out.println("\n소수 개수: " + primes.cardinality());
}
}
-
BitSet 장단점
장점 단점 메모리 1/8 사용 (1비트 vs 8비트) 비트 연산 오버헤드 대용량 처리에 유리 작은 범위에서는 느릴 수 있음 캐시 효율성 향상 코드 복잡도 증가 -
사용 권장 시기
- $n > 10^7$일 때
- 메모리 제약이 있을 때
- 여러 번 재사용할 때
세그먼티드 시브
- 매우 큰 범위의 소수를 찾을 때 메모리 문제를 해결하는 기법임
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
import java.util.ArrayList;
import java.util.Arrays;
public class SegmentedSieve {
/**
* 세그먼티드 시브: [low, high] 범위의 소수 찾기
* 메모리 복잡도: O(√n + segment_size)
*/
public static void segmentedSieve(long low, long high) {
// 1단계: √high까지의 소수 생성
int limit = (int) Math.sqrt(high) + 1;
boolean[] basePrimes = new boolean[limit + 1];
Arrays.fill(basePrimes, true);
basePrimes[0] = basePrimes[1] = false;
for (int i = 2; i * i <= limit; i++) {
if (basePrimes[i]) {
for (int j = i * i; j <= limit; j += i) {
basePrimes[j] = false;
}
}
}
// 기본 소수 목록 추출
ArrayList<Integer> primes = new ArrayList<>();
for (int i = 2; i <= limit; i++) {
if (basePrimes[i]) {
primes.add(i);
}
}
// 2단계: 세그먼트별로 처리
int segmentSize = (int) Math.min(100000, high - low + 1);
boolean[] segment = new boolean[segmentSize];
for (long segStart = low; segStart <= high; segStart += segmentSize) {
long segEnd = Math.min(segStart + segmentSize - 1, high);
Arrays.fill(segment, true);
// 각 소수로 세그먼트 체질
for (int prime : primes) {
// 세그먼트 내에서 prime의 첫 배수 찾기
long start = Math.max(prime * prime,
((segStart + prime - 1) / prime) * prime);
for (long j = start; j <= segEnd; j += prime) {
segment[(int)(j - segStart)] = false;
}
}
// 세그먼트의 소수 출력
for (long i = segStart; i <= segEnd; i++) {
if (i >= 2 && segment[(int)(i - segStart)]) {
System.out.print(i + " ");
}
}
}
}
public static void main(String[] args) {
System.out.println("10억~10억+1000 범위의 소수:");
segmentedSieve(1000000000L, 1000001000L);
}
}
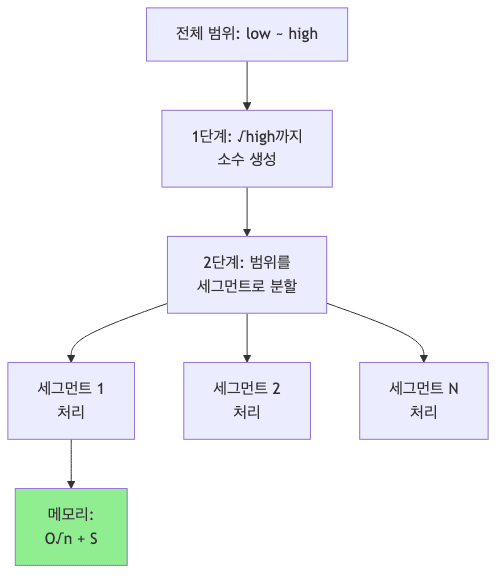
-
세그먼티드 시브 장점
- 메모리 $O(n) \rightarrow O(\sqrt{n} + S)$
- $10^9$ 이상의 범위도 처리 가능
- 캐시 효율성 향상
- 병렬화 가능
활용 예제
소수 개수 세기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import java.util.Arrays;
public class CountPrimes {
/**
* LeetCode 204: Count Primes
* n 미만의 소수 개수를 반환
*/
public static int countPrimes(int n) {
if (n <= 2) return 0;
boolean[] isPrime = new boolean[n];
Arrays.fill(isPrime, true);
isPrime[0] = isPrime[1] = false;
for (int i = 2; i * i < n; i++) {
if (isPrime[i]) {
for (int j = i * i; j < n; j += i) {
isPrime[j] = false;
}
}
}
int count = 0;
for (boolean prime : isPrime) {
if (prime) count++;
}
return count;
}
public static void main(String[] args) {
System.out.println("10 미만의 소수 개수: " + countPrimes(10)); // 4
System.out.println("100 미만의 소수 개수: " + countPrimes(100)); // 25
System.out.println("1000 미만의 소수 개수: " + countPrimes(1000)); // 168
}
}
범위 내 소수 찾기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class FindPrimesInRange {
/**
* [start, end] 범위의 소수를 리스트로 반환
*/
public static List<Integer> findPrimes(int start, int end) {
boolean[] isPrime = new boolean[end + 1];
Arrays.fill(isPrime, true);
isPrime[0] = isPrime[1] = false;
for (int i = 2; i * i <= end; i++) {
if (isPrime[i]) {
for (int j = i * i; j <= end; j += i) {
isPrime[j] = false;
}
}
}
List<Integer> result = new ArrayList<>();
for (int i = Math.max(2, start); i <= end; i++) {
if (isPrime[i]) {
result.add(i);
}
}
return result;
}
public static void main(String[] args) {
List<Integer> primes = findPrimes(50, 100);
System.out.println("50~100 사이의 소수: " + primes);
// 출력: [53, 59, 61, 67, 71, 73, 79, 83, 89, 97]
}
}
소인수분해
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
import java.util.Arrays;
public class PrimeFactorization {
/**
* 에라토스테네스의 체를 이용한 소인수분해
*/
public static void factorize(int n) {
// 1단계: √n까지의 소수 생성
int limit = (int) Math.sqrt(n) + 1;
boolean[] isPrime = new boolean[limit + 1];
Arrays.fill(isPrime, true);
for (int i = 2; i * i <= limit; i++) {
if (isPrime[i]) {
for (int j = i * i; j <= limit; j += i) {
isPrime[j] = false;
}
}
}
// 2단계: 소인수분해
System.out.print(n + " = ");
int temp = n;
boolean first = true;
for (int i = 2; i <= limit && temp > 1; i++) {
if (isPrime[i]) {
while (temp % i == 0) {
if (!first) System.out.print(" × ");
System.out.print(i);
temp /= i;
first = false;
}
}
}
// 남은 수가 1보다 크면 그것도 소수
if (temp > 1) {
if (!first) System.out.print(" × ");
System.out.print(temp);
}
System.out.println();
}
public static void main(String[] args) {
factorize(84); // 84 = 2 × 2 × 3 × 7
factorize(100); // 100 = 2 × 2 × 5 × 5
factorize(2310); // 2310 = 2 × 3 × 5 × 7 × 11
}
}
다른 소수 알고리즘과의 비교
단순 소수 판별 (Trial Division)
1
2
3
4
5
6
7
8
9
10
11
12
13
public static boolean isPrime(int n) {
if (n <= 1) return false;
if (n <= 3) return true;
if (n % 2 == 0 || n % 3 == 0) return false;
// 6k ± 1 형태만 확인
for (int i = 5; i * i <= n; i += 6) {
if (n % i == 0 || n % (i + 2) == 0) {
return false;
}
}
return true;
}
- 시간 복잡도
- $O(\sqrt{n})$ (개별 숫자당)
- 전체 복잡도
- $O(n\sqrt{n})$ (1~n까지 모든 소수)
- 사용 시기
- 단일 숫자의 소수 여부만 판별할 때
밀러-라빈 소수 판별 (Miller-Rabin)
- 시간 복잡도
- $O(k \log^3 n)$ (k는 반복 횟수)
- 특징
- 확률적 알고리즘
- 사용 시기
- $10^{18}$ 이상의 거대 소수 판별, 암호학
알고리즘 비교표
| 알고리즘 | 시간 복잡도 | 공간 복잡도 | 용도 |
|---|---|---|---|
| Trial Division | $O(n\sqrt{n})$ | $O(1)$ | 단일 숫자 판별 |
| 에라토스테네스 | $O(n \log \log n)$ | $O(n)$ | 범위 내 모든 소수 |
| 세그먼티드 시브 | $O(n \log \log n)$ | $O(\sqrt{n})$ | 대용량 범위 |
| 밀러-라빈 | $O(k \log^3 n)$ | $O(1)$ | 거대 소수 판별 |
| 선형 시브 | $O(n)$ | $O(n)$ | 이론적 최적 |