슬라이딩 윈도우 알고리즘

개요

• 슬라이딩 윈도우(Sliding Window)는 배열이나 문자열의 연속된 부분 집합을 효율적으로 처리하기 위한 알고리즘 기법임
• 창틀에 창문을 놓고 옆으로 밀면서 이동하는 모양에서 이름이 유래됨
• 두 개의 중첩 루프를 단일 루프로 변환하여 $O(N^2)$의 시간 복잡도를 $O(N)$으로 개선하는 것이 주요 목적임
• 이전 윈도우의 결과를 재사용하여 중복 연산을 방지하는 방식임

작동 원리

• 특정 범위(윈도우)를 지정하여 전체 배열 위를 미끄러지듯 이동하며 연산을 수행함
• 배열의 크기가 1,000,000 이상으로 매우 커서 $O(N)$의 시간 복잡도가 필수적인 상황에 효과적임
• 현재 윈도우와 다음 윈도우의 겹치는 부분을 활용함
• 윈도우 이동 시 빠져나가는 원소 하나를 제거하고 새로 들어오는 원소 하나를 추가하여 결과를 업데이트함

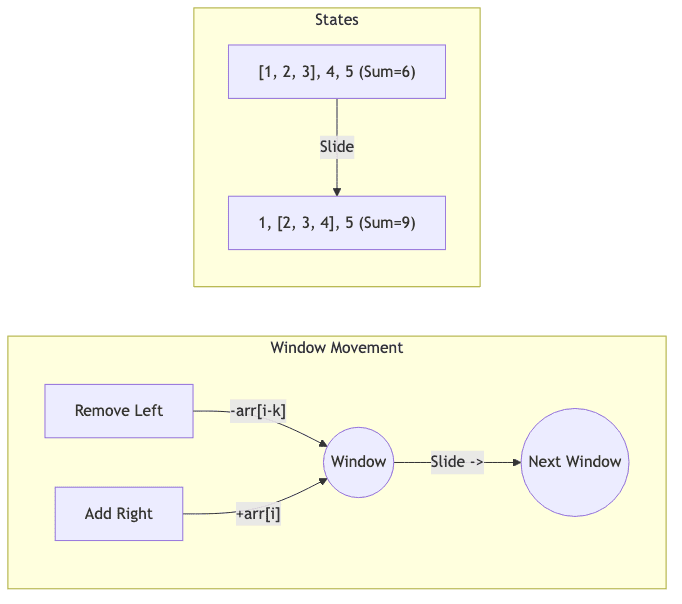
슬라이딩 윈도우의 유형

고정 크기 슬라이딩 윈도우

• 윈도우의 크기($K$)가 사전에 정해진 경우에 사용함
• 윈도우를 한 칸씩 이동하며 빠지는 값과 들어오는 값을 처리함

• ex)

  • 배열 [1, 3, 2, 6, -1, 4, 1]에서 $K=5$인 구간의 최대 합 도출

    // 고정 크기 윈도우 갱신 공식
    현재_합 = 현재_합 - arr[i - k] + arr[i]
    

가변 크기 슬라이딩 윈도우

• 문제의 조건에 따라 윈도우의 크기가 동적으로 변하는 방식임
• 두 개의 포인터(left, right)를 활용하여 범위를 조절함
• 조건 만족 시 right를 이동하여 확장하고 조건 위반 시 left를 이동하여 축소함
• 각 원소가 최대 2번만 방문되므로 $O(N)$의 효율성을 유지함

문제 식별 방법

• 특정 조건을 만족하는 알고리즘 적용 여부를 판단하는 기준임
• 배열, 리스트, 문자열 등 선형 데이터 구조를 다룸
• 부분 배열 또는 부분 문자열에서 최댓값, 최솟값 도출이 필요함
• 특정 조건을 만족하는 범위를 탐색함
• $O(N)$ 수준의 낮은 시간 복잡도가 요구됨
• 입력 크기($N$)가 $10^6$ 수준 이상으로 대량인 경우임

실제 적용

최장 부분 문자열 (중복 문자 없음)

• 주어진 문자열에서 반복되는 문자가 없는 가장 긴 부분 문자열의 길이를 구하는 문제

• 가변 크기 윈도우를 사용하여 좌우 경계를 조절하며 탐색함

  public int lengthOfLongestSubstring(String s) {
      int n = s.length();
      if (n == 0) return 0;
  
      int maxLength = 0;
      boolean[] visited = new boolean[128]; // 아스키 코드 기준
      int left = 0;
  
      for (int right = 0; right < n; right++) {
          char c = s.charAt(right);
  
          // 반복 문자 발견 시 왼쪽 포인터 이동하여 축소
          while (visited[c]) {
              visited[s.charAt(left)] = false;
              left++;
          }
  
          visited[c] = true;
          maxLength = Math.max(maxLength, right - left + 1);
      }
  
      return maxLength;
  }
  

최소 윈도우 부분 문자열

• 문자열 S에서 문자열 T의 모든 문자를 포함하는 최소 길이의 구간을 찾는 문제
• 해시맵을 활용하여 필요한 문자의 개수를 추적하며 윈도우를 조절함

덱(Deque) 활용

• 슬라이딩 윈도우 내에서 최솟값 혹은 최댓값을 빠르게 찾아야 할 때 사용하는 기법임

정렬의 한계와 필요성

• 데이터 범위가 $N, L = 5,000,000$ 수준으로 방대할 경우 일반적인 정렬을 사용할 수 없음
• 일반 정렬인 $O(N \log N)$은 시간 초과를 유발하므로 반드시 $O(N)$의 시간 복잡도가 요구됨
• 슬라이딩 윈도우의 범위가 $i-L+1$부터 $i$까지일 때 매번 정렬하는 대신 덱을 사용하여 정렬 효과를 얻음

덱(Deque)의 구조

• 양 끝에서 데이터의 삽입과 삭제가 모두 가능한 자료구조임
• 주요 함수
  • addFirst(), removeFirst()
    • 왼쪽(앞)에서 데이터 처리함
  • addLast(), removeLast()
    • 오른쪽(뒤)에서 데이터 처리함
• 덱을 활용하여 윈도우에서 필요 없는 데이터를 제거함으로써 최적값을 선형 시간 내에 유지함

구현 시 주의사항

인덱스 범위 계산 (Off-by-One 에러)

• 윈도우 크기 계산 시 양 끝점을 포함하기 위해 right - left + 1 공식을 사용함
• 단순 거리인 right - left와 혼동하지 않도록 함

초기 상태 설정

• 고정 크기 윈도우의 경우 루프 시작 전 반드시 첫 번째 윈도우($0$부터 $K-1$까지)를 별도 계산함

• 초기화된 값을 바탕으로 슬라이딩을 시작하여 누락을 방지함

  // 초기 윈도우 계산
  int windowSum = 0;
  for (int i = 0; i < k; i++) {
      windowSum += arr[i];
  }
  int maxSum = windowSum;
  
  // 슬라이딩 수행
  for (int i = k; i < n; i++) {
      windowSum = windowSum - arr[i - k] + arr[i];
      maxSum = Math.max(maxSum, windowSum);
  }
  

투 포인터와의 차이점

• 두 기법은 모두 2개의 포인터를 사용하지만 구간 처리 방식에서 차이가 발생함

  구분	투 포인터 (Two Pointers)	슬라이딩 윈도우 (Sliding Window)
  구간 형태	비연속적인 쌍을 다루기도 함	항상 연속적인 구간을 다룸
  윈도우 크기	가변적이며 조건에 따라 증감함	주로 고정적인 크기를 유지함
  이동 방식	포인터가 서로 반대 방향으로도 움직임	포인터가 일정한 간격을 유지하며 순방향 이동함

요약 정리

• 중복 연산을 제거하여 선형 시간 복잡도를 달성하는 효율적인 탐색 기법임
• 구간의 합, 평균, 또는 특정 조건의 문자열을 찾는 데 최적화되어 있음
• 포인터의 이동 조건과 윈도우 크기 유지 방식에 대한 명확한 설계가 필요함

Reference

• Do it! 알고리즘 코딩 테스트 - 자바 편