학습 개요
- 기본적인 형태의 정렬 알고리즘에 비해서 향상 된 성능을 가진 퀵 정렬과 합병 정렬에 대해서 학습함
- 저장 된 데이터에 대해서 원하는 데이터를 찾는 탐색의 다양한 방법들의 개념, 동작, 특징을 살펴봄
학습 목표
- 퀵 정렬과 합병 정렬의 개념, 동작, 그리고, 특징을 이해할 수 있음
- 순차 탐색과 이진 탐색의 개념, 동작, 그리고 특징을 이해할 수 있음
- 이진 탐색 트리의 개념, 연삭(탐색, 삽입, 삭제), 그리고 성능을 이해할 수 있음
강의록
정렬 알고리즘: 퀵 정렬, 합병 정렬
퀵 정렬
- 특정 데이터를 기준으로 입력 배열을 두 부분 배열로 분할하고, 각 부분 배열에 대해서 독립적으로 퀵 정렬을 순환적으로 적용
- 평균적으로 가장 좋은 성능의 비교 기반 알고리즘
- O(nlogn)
- 피벗(plvot, 분할 원소)
- 두 개의 부분 배열로 분할할 때 기준이 되는 데이터
- 보통 주어진 배열의 첫 번째 원소로 지정
-
피벗이 제자리를 잡도록 하여 정렬하는 방식
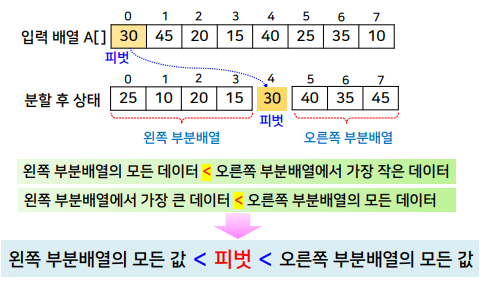
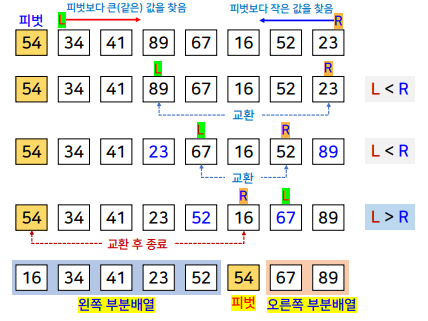
분할 과정
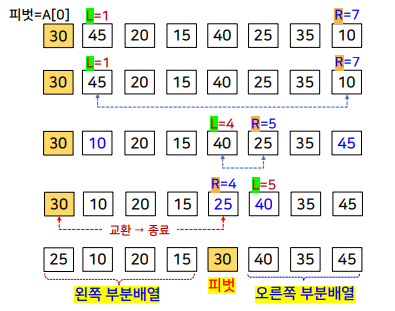
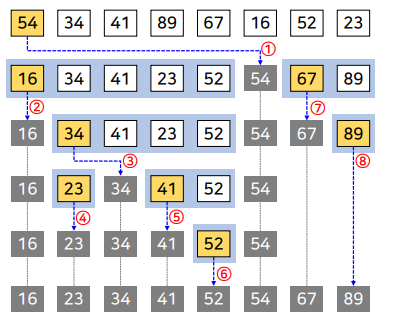
퀵 정렬의 전체적인 수행 과정
퀵 정렬의 특징
- 분할 정복 방법을 적용한 알고리즘
- 분할
- 정렬할 n개의 데이터를 피벗을 중심으로 두 개의 부분 배열로 분할
- 정복
- 두 부분 배열 각각에 대해 퀵 정렬을 순환적으로 적용하여 두 부분 배열을 정렬
- 결합
- 필요 없음
- 분할
- 성능
- 분할 과정의 수행 시간
- O(n)
- 평균 수행 시간
- O(nlogn)
- 최선 수행 시간
- O(nlogn)
-
피벗을 중심으로 항상 동일한 크기의 두 부분 배열로 분할 되는 경우
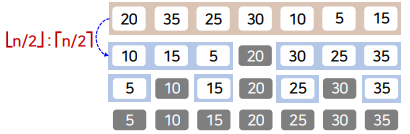
- 최악 수행 시간
- O(n²)
- 피벗 선택의 임의성만 보장되면 평균 수행 시간을 보일 가능성이 높음
-
피벗만 제자리를 잡고 나머지 모든 데이터가 하나의 부분 배열로 분할되는 경우
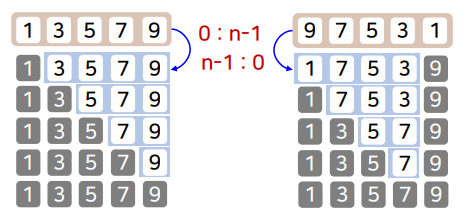
- 피벗이 배열에서 항상 최솟값이나 최댓 값이 되는 경우
- 입력 데이터가 이미 정렬된 경우 AND 피벗을 첫 번째 원소로 지정한 경우
- O(n²)
- 분할 과정의 수행 시간
합병 정렬
-
동일한 크기의 두 개의 부분 배열로 분할하고, 각 부분 배열을 순환적으로 정렬한 후, 정렬된 두 부분 배열을 합병해서 하나의 정렬된 배열을 만드는 방식
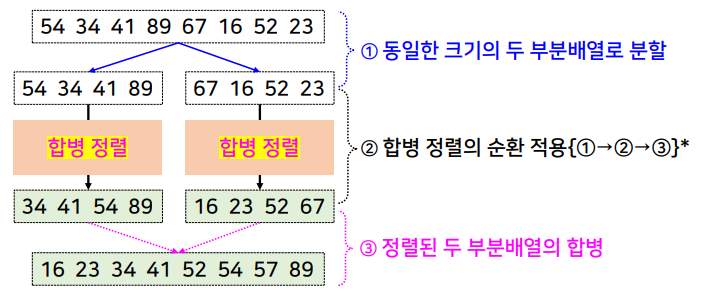
합병 정렬의 전체적인 수행 과정
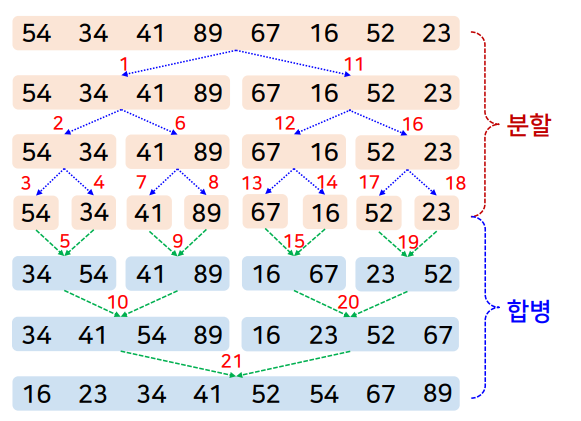
- 분할
- 주어진 배열을 더 이상 분할할 수 없을 때까지 절반으로 나눔
- 합병 정렬의 순환적 적용
- 분할 된 각 부분 배열에 대해 재귀적으로 합병 정렬을 적용
- 정렬된 두 부분 배열의 합병
- 정렬된 부분 배열들을 합쳐 하나의 정렬된 배열을 만듦
합병 과정
-
정렬된 두 부분 배열을 하나의 정렬된 배열로 만드는 과정
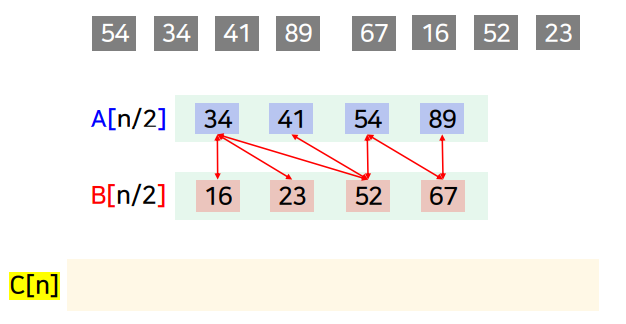
합병 정렬의 특징
- 분할 정복 방법을 적용한 알고리즘
- 분할
- 정렬할 n개의 데이터를 n/2개의 데이터를 갖는 두 부분 배열로 분할
- 정복
- 두 부분 배열에 대해 합병 정렬을 각각 순환적으로 적용하여 정렬
- 합병
- 정렬 된 두 부분 배열을 합병하여 하나의 정렬된 배열을 만듦
- 최선, 최악, 평균 수행 시간
- O(nlogn)
순차 탐색, 이진 탐색
탐색
- 주어진 데이터 집합에서 원하는 값을 가진 데이터를 찾는 작업
- 순차 탐색 (sequential search)
- O(n)
- 이진 탐색 (binary search)
- O(logn)
- 이진 탐색 트리 (binary search tree)
- 평균 O(logn)
- 최악 O(n)
- 순차 탐색 (sequential search)
순차 탐색
-
리스트 형태로 주어진 데이터를 처음부터 하나씩 차례대로 비교하여 원하는 데이터를 찾는 방법
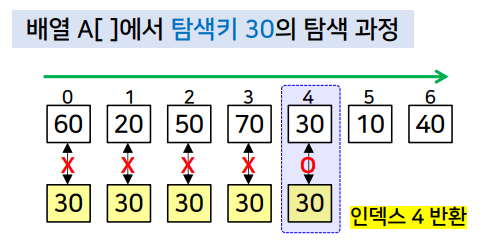
- 배열의 첫 번째 원소부터 순서대로 탐색키 30과 비교
- A[0]부터 A[3]까지 30과 일치하지 않음
- A[4]에서 30을 찾아 인덱스 4를 반환
순차 탐색의 특징
- 탐색 성능
- O(n)
- 실패하는 경우의 비교 횟수
- n번
- 성공하는 경우의 비교 횟수
- 1∼n번
- 평균 n+1/2 번
- 모든 리스트(배열, 연결 리스트)에 적용 가능
- 데이터가 키 값과 관련해서 아무런 순서 없이 단순하게 연속적으로 저장
- 데이터가 정렬되지 않은 경우에 적합
- 데이터가 키 값과 관련해서 아무런 순서 없이 단순하게 연속적으로 저장
이진 탐색
- 정렬된 입력 배열에 대해서 주어진 데이터를 절반씩 줄여가면서 원하는 데이터를 찾는 방법
- 분할 정복 방법을 적용한 알고리즘
- 탐색 방법
- 입력 배열의 가운데 값
A[Mid]와 탐색 키key를 비교- $Mid = \left\lfloor \frac{\text{Left} + \text{Right}}{2} \right\rfloor$
key = A[Mid]- 탐색 성공
- 배열의 인덱스 Mid 반환
key < A[Mid]- 이진 탐색
- 원래 크기의 1/2인 왼쪽 부분 배열
key > A[Mid]- 이진 탐색
- 원래 크기의 1/2인 오른쪽 부분 배열
- 탐색을 반복할 때마다 대상 원소의 개수가 1/2씩 감소
- 입력 배열의 가운데 값
이진 탐색의 탐색 과정

Left=0,Right=8,탐색키 key=35인 배열[10, 15, 20, 2W5, 30, 35, 40, 45, 50]에서key=35를 찾는 과정Mid값을 계산하여A[Mid]와key를 비교하며 탐색 범위를 좁혀 나감A[Mid] < key이면 오른쪽 부분 배열을 다시 탐색 (Left 조정)key < A[Mid]이면 왼쪽 부분 배열을 다시 탐색 (Right 조정)key = A[Mid]이면 탐색 성공,Mid값을 반환
이진 탐색의 특징
- 성능
- O(logn)
- 한 번 탐색할 때마다 탐색 대상이 되는 데이터의 개수가 1/2씩 감소
- 데이터가 이미 정렬된 경우에만 적용 가능
- 삽입/삭제 연산 시 정렬 상태의 유지를 위해 데이터 이동이 발생
- 삽입/삭제와 같은 동적 연산이 많은 응용에는 부적합
이진 탐색 트리
- 다음의 두 성질을 만족하는 이진 트리
- 각 노드의 왼쪽 서브 트리에 있는 모든 키 값은 그 노드의 키 값보다 작음
- 각 노드의 오른쪽 서브 트리에 있는 모든 키 값은 그 노드의 키 값보다 큼
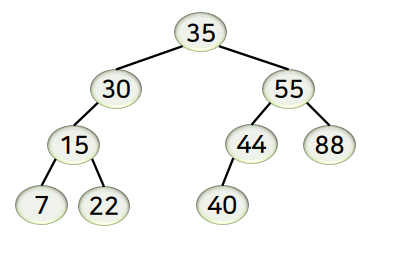
탐색 연산
-
루트 노드에서부터 키 값의 비교를 통해 왼쪽 또는 오른쪽 서브 트리를 따라 이동하면서 데이터를 찾음
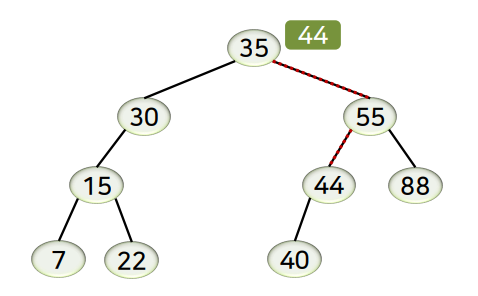
삽입 연산
- 삽입할 데이터를 탐색한 후, 탐색이 실패한 위치에 새로운 노드를 자식 노드로 추가
- 탐색이 성공한 경우 → 데이터가 이미 존재하므로 삽입 없이 종료
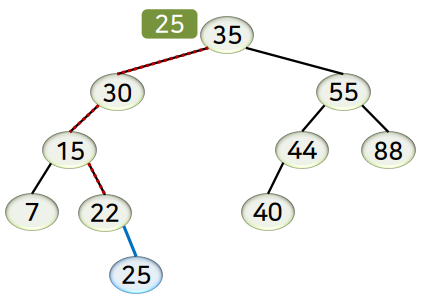
삭제 연산
- 후속자 노드 (successor, 계승자 노드)
- 어떤 노드의 키 값 바로 다음 키 값을 갖는 노드
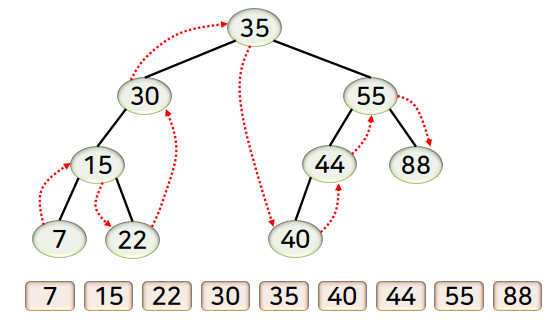
- 삭제되는 노드의 자식 노드의 개수에 따라 구분해서 처리
- 자식 노드가 없는 경우 (리프 노드의 경우)
- 남는 노드가 없으므로 위치 조절이 불필요
- 자식 노드가 1개인 경우
- 자식 노드를 삭제되는 노드의 위치로 올리면서 서브 트리 전체도 따라 올림
- 자식 노드가 2개인 경우
- 삭제되는 노드의 후속자 노드를 삭제되는 노드의 위치로 올리고, 후속자 노드를 삭제되는 노드로 취급하여 자식 노드의 개수에 따라 다시 처리
- 자식 노드가 없는 경우 (리프 노드의 경우)
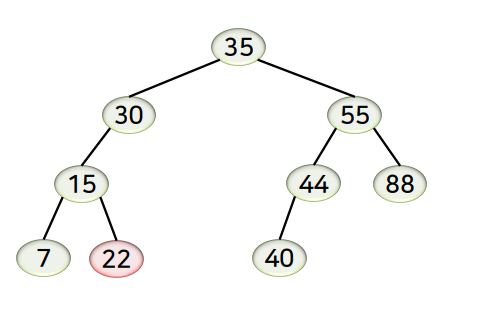
- 노드 22 삭제
- 자식 노드가 없는 경우 (리프 노드)에 해당하며, 해당 노드만 제거함
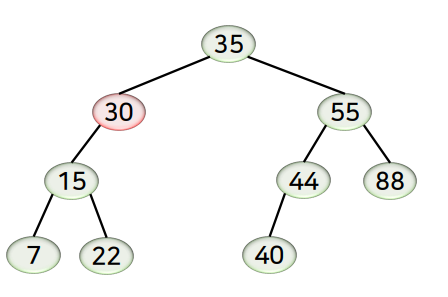
- 노드 30 삭제
- 자식 노드가 2개인 경우에 해당하며, 후속자 노드를 30의 위치로 올리고 35가 기존에 있던 위치를 처리함
- 노드 55 삭제
- 자식 노드가 2개인 경우에 해당하며, 후속자 노드를 55의 위치로 올리고 60이 기존에 있던 위치를 처리함
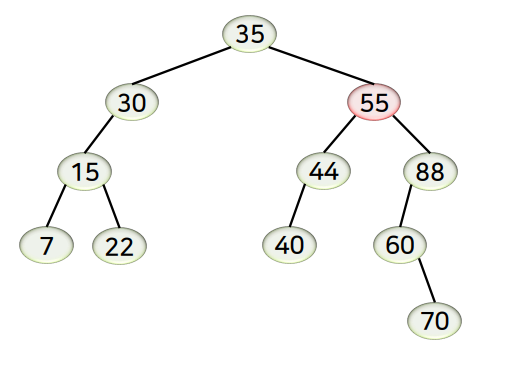
성능
- 키 값의 비교 횟수에 비례
- 트리의 높이 h
- O(h)
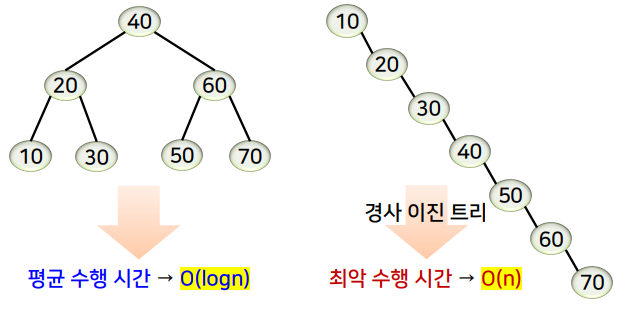
- 트리의 높이 h
정리 하기
- 정렬 알고리즘: 퀵 정렬, 합병 정렬
- 퀵 정렬
- 분할 정복 방법
- 피벗
- 분할 과정
- O(nlogn)
- O($n^2$)
- 합병 정렬
- 분할 정복 방법
- 합병 과정
- O(nlogn)
- 퀵 정렬
- 순차 탐색, 이진 탐색
- 순차 탐색
- 비정렬 데이터에 적합
- 데이터가 큰 경우 부적합
- O(n)
- 이진 탐색
- 정렬된 입력 배열에 대해서만 적용 가능
- 삽입/삭제가 빈번한 응용은 부적합
- O(logn)
- 순차 탐색
- 이진 탐색 트리
- 두 가지 성질을 만족하는 이진 트리
- 연산
- 탐색, 삽입, 삭제(후속자 노드, 자식 노드의 개수에 따라 구분)
- 최선/평균 탐색 시간
- O(logn)
- 최악 탐색 시간
- O(n)
연습 문제
-
퀵 정렬에 대한 설명으로 틀린 것은?
a. 항상 동일한 크기의 두 부분 배열로 분할 된다.
- 합병 정렬에 대한 설명임
- 퀵 정렬은 피벗이라는 특정 데이터를 기준으로 분할하기 때문에 왼쪽과 오른쪽 부분 배열의 크기가 일정하지 않음
- 퀵 정렬에 대한 설명으로 옳은 것
- 분할 정복 방법을 적용함
- 최악의 시간 복잡도는 O(n²)임
- 최선 수행 시간은 O(nlogn)임
-
주어진 데이터에 대해 퀵 정렬의 분할 과정을 한 번 적용한 후의 왼쪽 부분 배열의 첫 번째 데이터는?(단, 배열의 첫 번째 원소를 피벗으로 사용한다.)
1
35 26 15 77 10 61 11 59 17 48 19 40
a. 10
-
주어진 데이터에 대해서 두 부분 배열로 분할하는 과정은 다음과 같음

-
-
합병 정렬 알고리즘의 합병(merge) 과정에 입력으로 주어지는 두 부분 배열 X, Y는 어떠한 상태이어야 하는가?
a. X, Y 각각 제 순서로 정렬되어 있어야 한다.
- 동일한 크기로 분할 된 두 부분 배열이 각각 정렬된 상태로 합병 과정의 입력으로 주어지면, 각 부분 배열의 원소를 앞에서부터 하나씩 서로 비교해서 작은 값을 우선 취해서 정렬된 부분에 포함 시키는 방식으로 합병이 이루어진다.
-
순차 탐색과 이진 탐색에 대한 설명으로 올바른 것은?
a. 순차 탐색은 정렬된 리스트에 적용할 수 있다.
- 이진 탐색에서는 삽입/삭제 시 정렬 상태를 유지하기 위해 데이터의 이동이 발생하므로, 삽입/삭제가 빈번한 응용에는 부적합함
- 순차 탐색과 이진 탐색의 성능은 각각 **O(n)과 O(logn)임
- 순차 탐색은 데이터가 정렬되지 않은 경우에 적합함
- 순차 탐색은 모든 리스트에 적용 가능하므로, 정렬된 리스트에도 적용할 수 있음
-
이진 탐색 트리에서 노드 30의 후속자 노드의 키 값은?
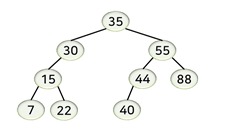
a. 35
- 어떤 노드의 바로 다음 키 값을 갖는 노드를 후속자(successor) 노드라고 함
-
이진 탐색 트리의 탐색 과정에 대한 최악의 시간 복잡도와 평균 시간 복잡도가 올바르게 짝지어진 것은?
a. O(n) - O(logn)
- 이진 탐색 트리의 평균 탐색 시간은 O(logn)이지만 이미 정렬된 순서로 데이터가 입력되어 경사 트리를 형성하는 경우에는 최악의 시간 복잡도 O(n)을 갖음
정리 하기
- 정렬 알고리즘
- 퀵 정렬과 합병 정렬
- 퀵 정렬
- 특정 데이터를 기준으로 주어진 입력 배열을 두 개의 부분 배열로 분할하고, 각 부분 배열에 대해서 독립적으로 퀵 정렬을 순환적으로 적용하는 방법
- 피벗이 제자리를 잡도록 정렬하는 방식
- 분할 정복을 적용한 알고리즘
- 피벗
- 두 개의 부분 배열로 분할할 때 기준이 되는 데이터
- 보통 배열의 첫 번째 원소를 피벗으로 지정
- 분할 과정
- 퀵 정렬의 가장 핵심 부분
- 피벗을 중심으로 두 부분 배열로 분할하는 과정
- O(n)
- 최선의 수행 시간
- 피벗을 중심으로 동일한 크기의 두 개의 부분 배열로 분할 되는 경우
- O(nlogn)
- 최악의 수행 시간
- 피벗 하나만 제자리를 잡고, 나머지 모든 데이터가 하나의 부분 배열로 분할 되는 경우 피벗이 배열에서 항상 최대 값이나 최소 값이 되는 경우
- 입력 데이터가 이미 정렬되어 있고 배열의 맨 왼쪽 원소를 피벗으로 사용하는 경우
- O(n2)
- 평균 수행 시간
- O(nlogn)
- 피벗 선택의 임의성만 확보되면 최악의 수행 시간이 아닌 평균 수행 시간이 보장됨
- 특정 데이터를 기준으로 주어진 입력 배열을 두 개의 부분 배열로 분할하고, 각 부분 배열에 대해서 독립적으로 퀵 정렬을 순환적으로 적용하는 방법
- 합병 정렬
- 동일한 크기의 두 개의 부분 배열로 분할하고 각 부분 배열을 순환적으로 정렬한 후 정렬 된 두 부분 배열을 합병하여 하나의 정렬된 리스트를 형성하는 방식
- 분할 정복을 적용한 알고리즘
- 합병 과정
- 정렬된 두 부분 배열을 입력으로 받아 하나의 정렬된 배열로 만드는 과정
- 최선/평균/최악 수행 시간
- O(nlogn)
- 순차 탐색과 이진 탐색
- 순차 탐색
- 리스트 형태로 주어진 데이터를 처음부터 하나씩 차례대로 비교하여 원하는 값을 가진 데이터를 찾는 방법
- 모든 리스트(배열, 연결 리스트)에 적용 가능, 특히 데이터가 정렬되지 않은 경우에 적합
- O(n)
- 이진 탐색
- 정렬된 입력 배열에 대해서 주어진 데이터를 절반씩 줄여가면서 원하는 데이터를 찾는 방법
- 분할 정복을 적용한 알고리즘
- 주어진 배열의 가운데 데이터의 값과 탐색 키를 비교
- 탐색 키 = 배열의 가운데 값이면 탐색 성공
- 탐색 키 < 배열의 가운데 값이면 주어진 배열의 전반부를 탐색 범위로 재지정한 후 이진 탐색을 순환 호출
- 탐색 키 > 배열의 가운데 값이면 주어진 배열의 후반부를 탐색 범위로 재지정한 후 이진 탐색을 순환 호출
- 탐색을 한 번 수행할 때마다 탐색 대상이 되는 원소의 개수가 절반씩 감소
- O(logn)
- 빈번한 삽제/삭제가 있는 응용에는 부적합
- 정렬 상태 유지를 위한 데이터 이동으로 인해 오버 헤드 발생
- 순차 탐색
- 이진 탐색 트리
- 이진 탐색 트리
- 각 노드 x의 왼쪽 서브 트리의 모든 키 값은 x의 키 값보다 작고, 오른쪽 서브 트리의 모든 키 값은 x의 키 값보다 크다는 조건을 만족 시키는 이진 트리
- 탐색 연산
- 루트 노드로부터 시작해서 값의 크기 관계에 따라 트리의 경로를 따라 내려가면서 원하는 키 값을 갖는 원소를 찾음
- 삽입 연산
- 삽입할 원소를 탐색한 후, 탐색이 실패한 지점의 왼쪽/오른쪽 자식 노드를 생성하여 추가
- 삭제 연산
- 삭제되는 자식 노드의 개수에 따라 3가지 경우로 구분해서 처리
- 자식 노드가 없는 경우
- 남은 노드의 위치 조절이 불필요
- 자식 노드가 하나인 경우
- 자식 노드를 삭제되는 노드의 위치로 올리면서 서브 트리 전체도 따라 올림
- 자식 노드가 두 개 모두 있는 경우
- 후속자 노드(어떤 노드의 바로 다음 키 값을 갖는 노드)를 삭제되는 노드의 위치로 올리고, 후속자 노드의 자식 노드의 개수에 따라 다시 삭제 연산을 처리
- 성능
- 평균 탐색 시간
- O(logn)
- 리프 노드를 제외한 모든 노드의 차수가 2인 경우
- 최악 탐색 시간
- O(n)
- 경사 이진 트리, 즉 리프 노드를 제외한 모든 노드의 차수가 1인 경우
- 평균 탐색 시간
- 이진 탐색 트리