학습 개요
- 엑셀 차트 기능을 활용하면 주어진 함수의 그래프를 그릴 수 있고, 목표 값 찾기 기능을 이용하여 주어진 함수가 축과 만나는 점을 찾을 수 있음
- 엑셀의 함수 기능을 활용하여 주어진 적분 값을 근사적으로 구하는 법을 익힘
- 엑셀을 활용하여 해결할 수 있는 다양한 예제를 살펴봄으로써 엑셀의 활용 능력을 높임
학습 목표
- 엑셀 함수 기능을 이용하여 원리 합계를 계산할 수 있음
- 엑셀 차트 기능을 이용하여 주어진 함수의 그래프를 그릴 수 있음
- 목표 값 찾기 기능을 활용할 수 있음
- 엑셀을 활용하여 적분 값을 계산할 수 있음
주요 용어
- 상대 참조
- 행 이름이나 열 이름만을 사용하여 셀을 참조하는 방법
- ex)
A1,B2,A1:F1등
- 절대 참조
- 참조하는 셀이나 셀 범위를 표시할 때 “
$“를 사용하여 참조하는 방법 - ex)
$A$1,$B$2,$A$1:$F$1등
- 참조하는 셀이나 셀 범위를 표시할 때 “
- 혼합 참조
- 행 이름이나 열 이름의 한 쪽에만 “$”를 사용하여 참조하는 방법
- ex)
$A1,B$2,A$1:F$1등
- 목표 값 찾기 기능
- 엑셀의 여러 기능 중 특정 수식 값을 목표하는 값(목표 값)과 같아지도록 수식과 관련된 입력 값을 조정하여 찾는 기능을 말함
강의록
원리 합계 계산
셀 참조 방법
- 상대 참조 (Relative Reference)
- 행 이름이나 열 이름만을 사용하여 셀을 참조함
- 수식을 복사하면 위치에 따라 참조가 변경 됨
- ex)
A1,D3,=AVERAGE(A2:G2)
- 절대 참조 (Absolute Reference)
- 참조하는 셀이나 셀 범위를 표시할 때
$표시를 사용함 - 수식을 복사해도 참조가 변경되지 않음
- ex)
$A$1,$D$3,=AVERAGE($A$2:$G$2)
- 참조하는 셀이나 셀 범위를 표시할 때
- 혼합 참조 (Mixed Reference)
- 행 이름이나 열 이름의 한쪽에만
$표시하여 참조함 - ex)
$A1(A열 고정, 행 변경 가능) - ex)
D$3(D열 변경 가능, 3행 고정) - ex)
=AVERAGE($A2:$G2)
- 행 이름이나 열 이름의 한쪽에만
원리 합계 계산 예제
- 복리로 계산 되는 경우에 현재 금액 p에 대한 일정 기간 후의 원리 합계 G는 연 이율을 r, 기간을 n으로 주어졌을 때 다음과 같이 계산 됨
G = p * (1+r)^
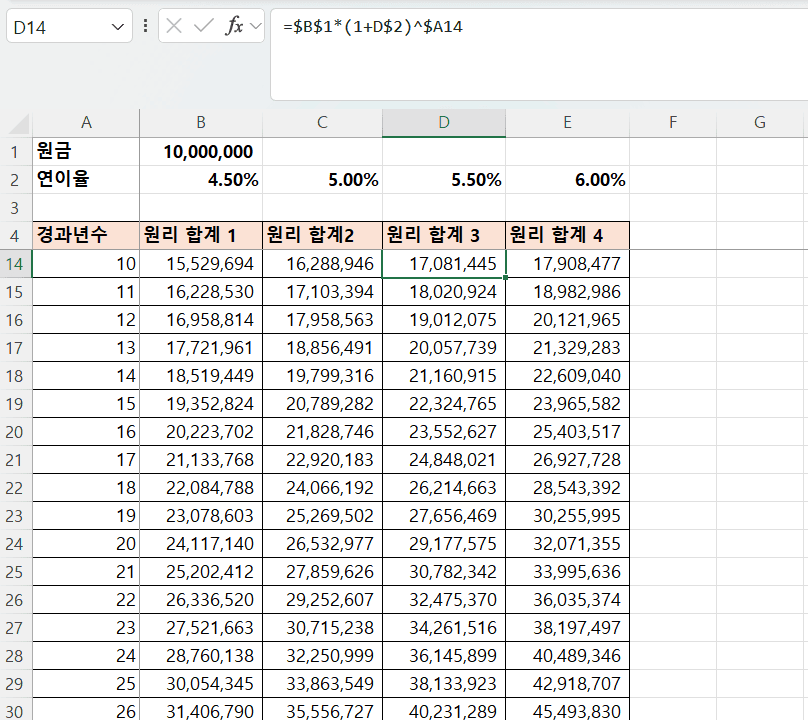
- 원금이 1,000만원인 경우 연 4.5%, 5.0%, 5.5%, 6.0%로 주어진 경우에 향후 20년이 경과하였을 때 원리 합계가 얼마나 차이가 생기는가?
- 기본 정보를 입력하고, 경과 년수는 채우기 기능을 이용하여 20까지 입력
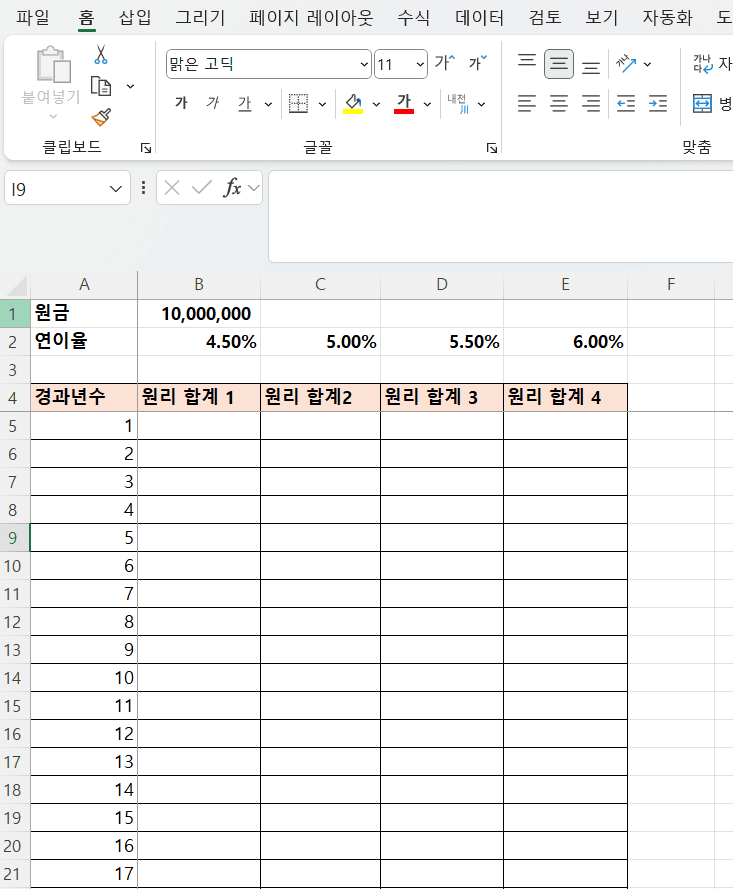
- 참고
- 함수 식에서 원리 합계를 구할 때 원금은 절대 참조 이용
- 함수 식에서 연 이율과 경과 년수는 혼합 참조 이용 참조
- B5 셀에
=$B$1*(1+B$2)^$A5을 입력하고, 채우기 기능을 이용하여 채움
- B5 셀에
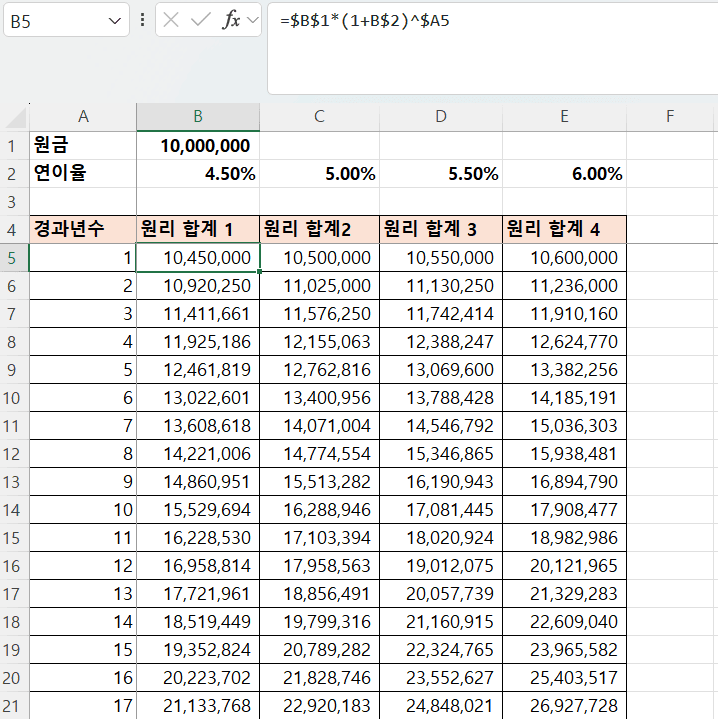
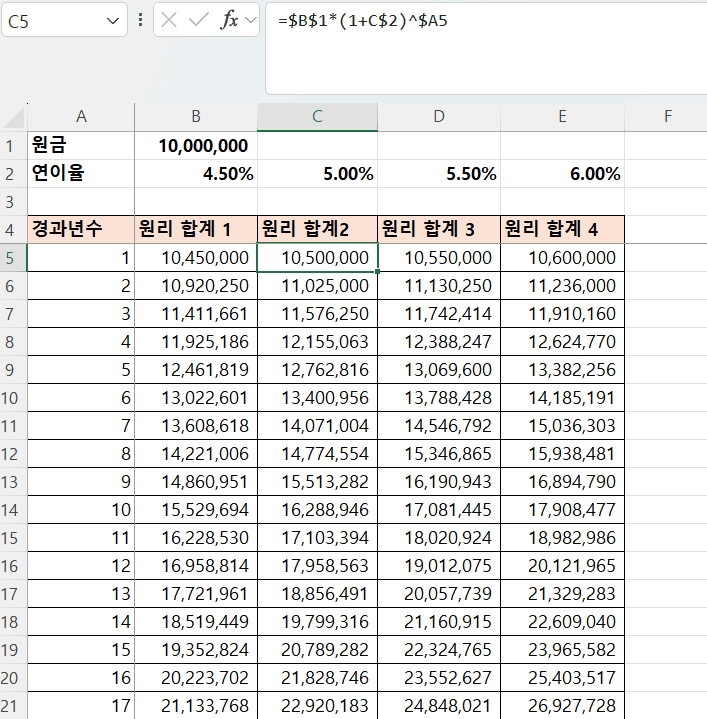
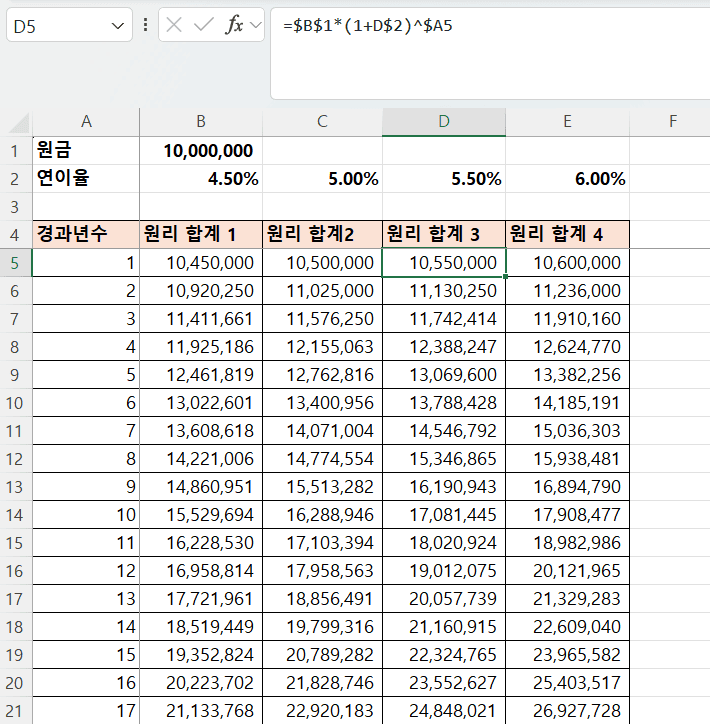
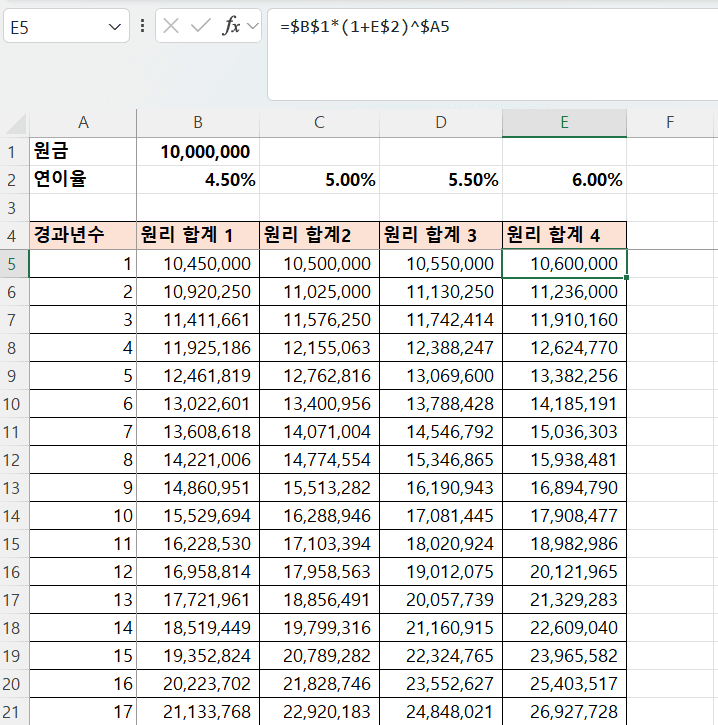
- 원금(
$B$1)은 항상 고정- 절대 참조
$B$1
- 절대 참조
- 연 이율(
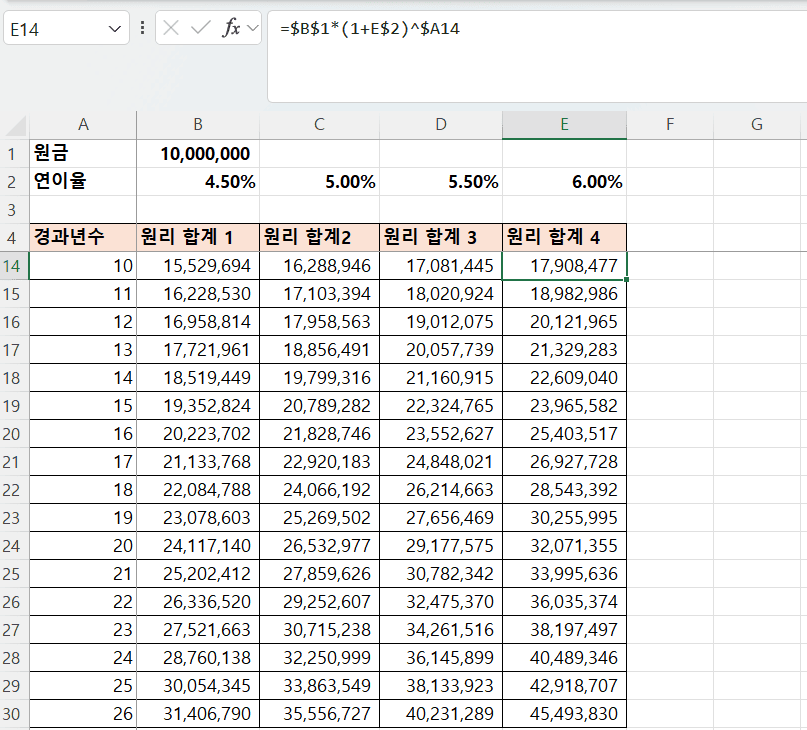
B$2,C$2, …)은 열 별로 다르지만 행은 고정- 혼합 참조
B$2 - 열은 상대, 행은 절대
- 혼합 참조
- 경과 년수(
$A5,$A6, …)는 행 별로 다르지만 열은 고정- 혼합 참조
$A5 - 열은 절대, 행은 상대
B5:E5까지 선택하고 드래그 & 드롭으로 20년이 경과한 후까지 채움- 채우기를 마친 후
B5셀을 선택하여 [보기]-[창] 그룹에서 [틀 고정]을 선택
- 혼합 참조
- [틀 고정] 기능을 이용하면 워크 시트를 읽을 때 편리함
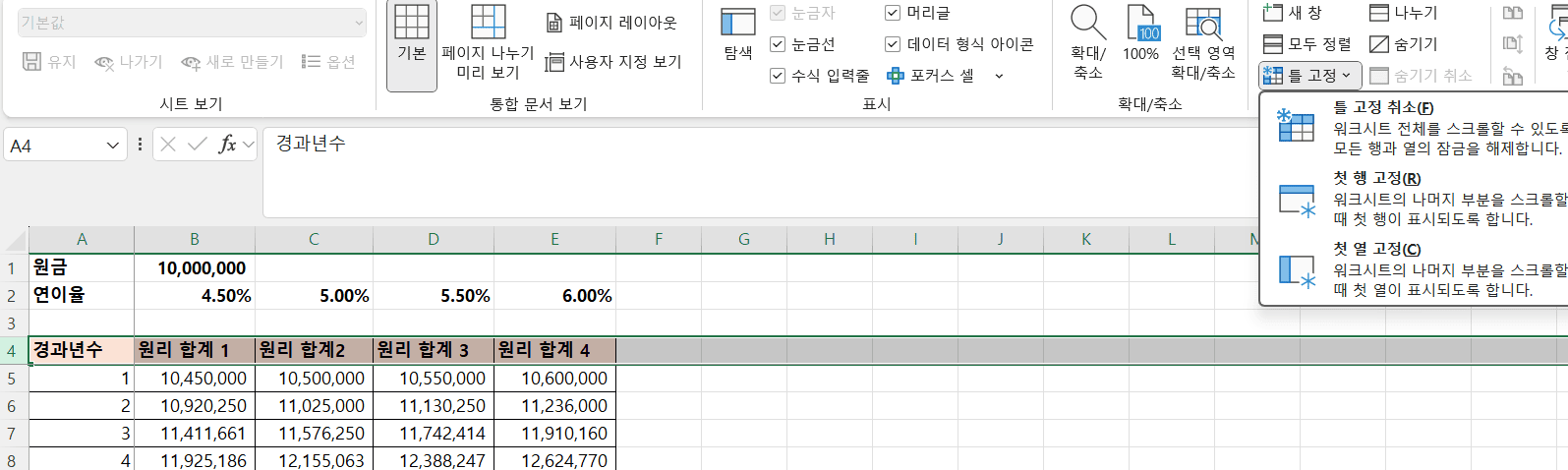
-
연 이율 1%의 차이가 20년 후에 약 500만원 이상의 차이로 나타남
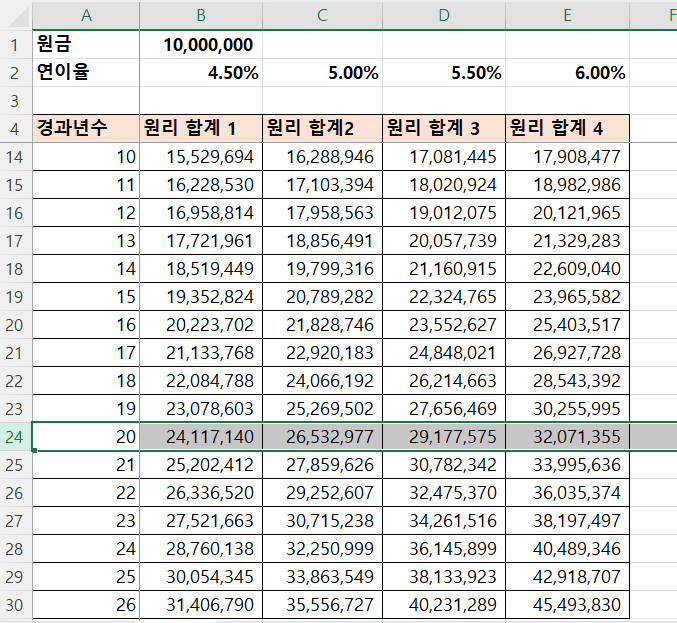
함수 그래프 그리기와 해 찾기
엑셀을 활용한 함수 그래프 그리기, 해 찾기
- 함수 기능과 차트 기능을 활용하면 간단한 함수의 그래프 개형 뿐만 아니라 방정식의 해도 구할 수 있음
- 예제: 함수의 그래프 개형을 구간 (-3, 3) 에서 그려보고 그 구간에서 만족하는 근사적인 해 찾기
함수 그래프 그리기
- -3.0부터 3.0까지 0.1 간격으로 채우기 기능 실행
-
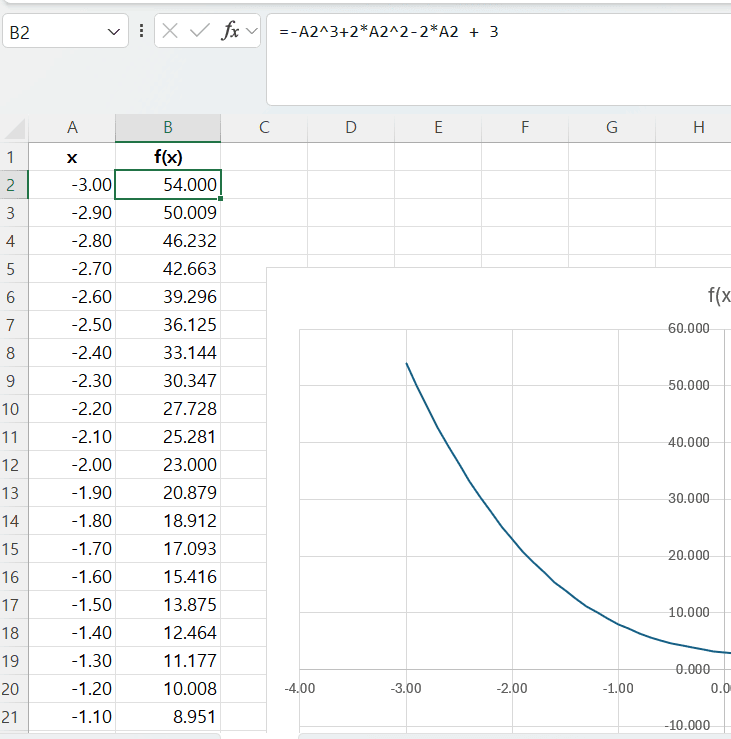
B2셀에는=-A2^3 + 2*A2^2 - 2*A2 + 3을 입력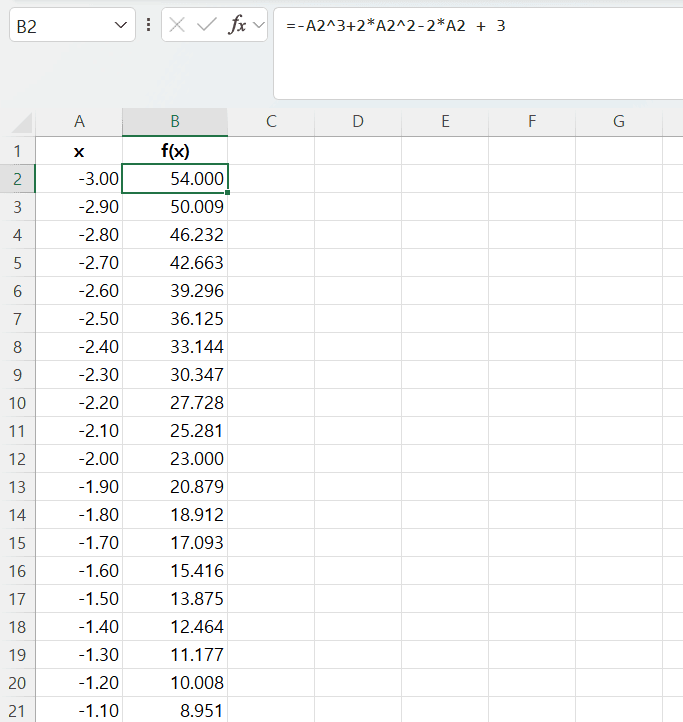
- 나머지 셀들에 대해서 드래그 & 드롭을 통해서 채워 넣음
- (-3, 3) 범위에서 함수의 그래프 그리기
- 차트 종류 중 분산형 선택
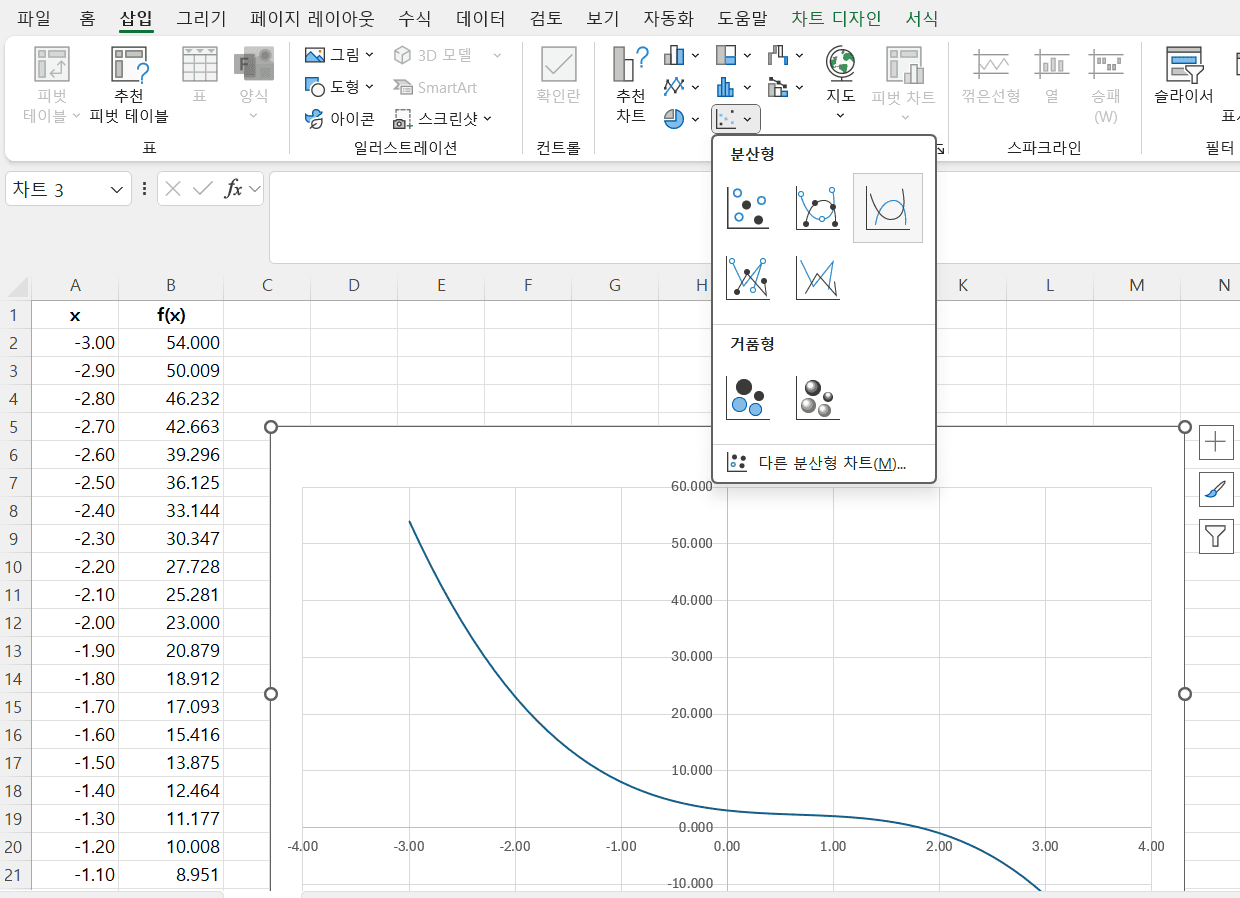
-
차트의 종류 중에서 분산형을 선택하여 그래프 작성
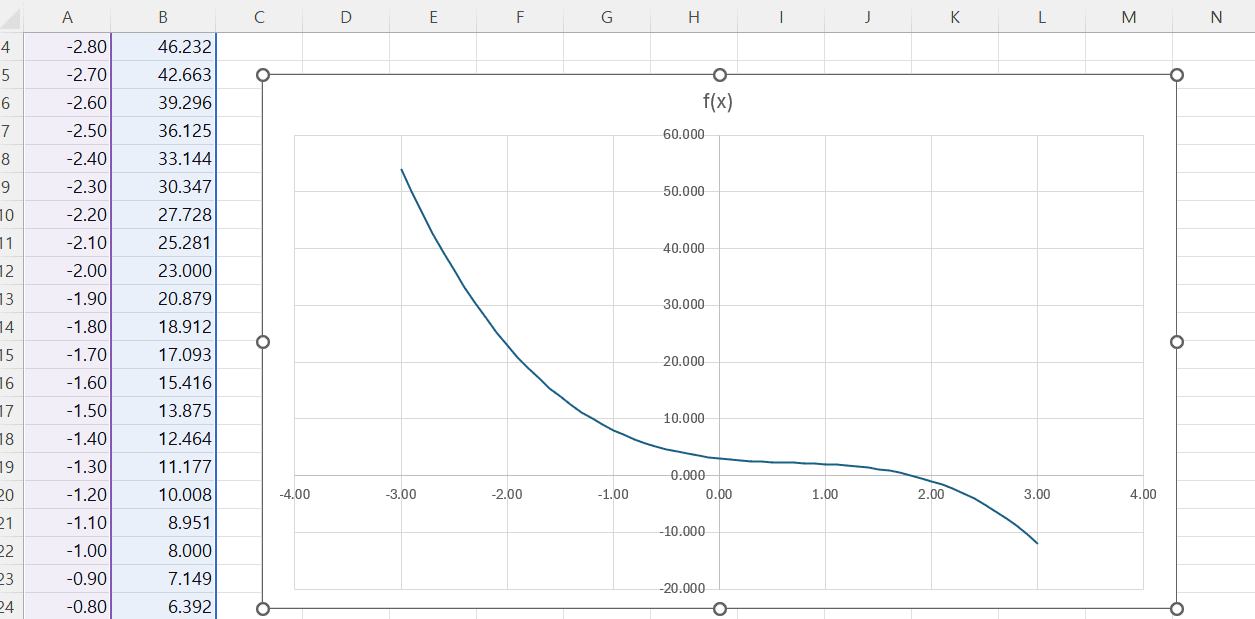
목표 값 찾기 기능을 이용하여 해 찾기
- 함수 f(x) = -x^3 + 2x^2 - 2x + 3을 만족하는 정확한 해는 엑셀 목표 값 찾기 기능을 이용하면 편리하게 구할 수 있음
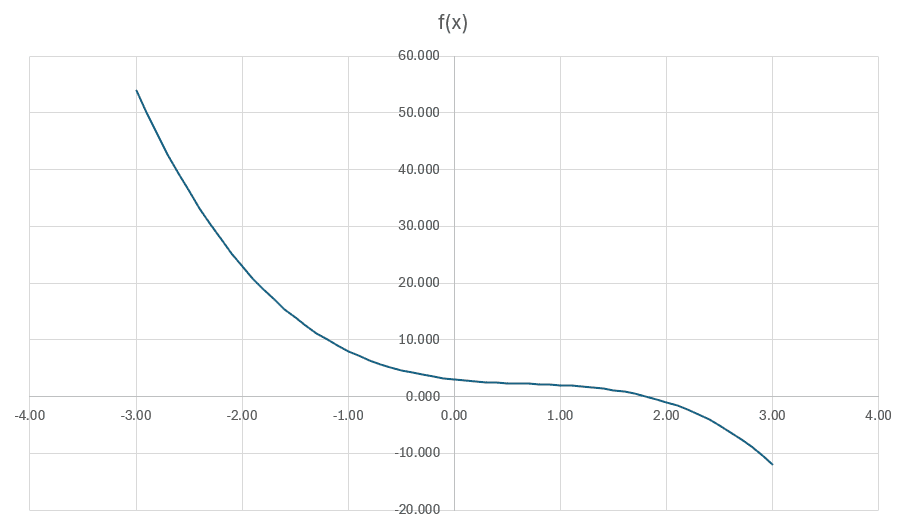
-
함수 그래프 그리기를 통해서 함수 f(x) = -x^3 + 2x^2 - 2x + 3의의 근사적인 해는 1.8 근처의 값임을 알 수 있음
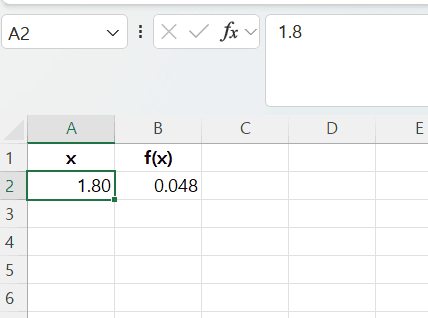
- 워크 시트에 구하고자 하는 함수 식에 대한 근사적 해를 입력함.
- 편의 상
A2셀에 1.8를 입력
- 편의 상
-
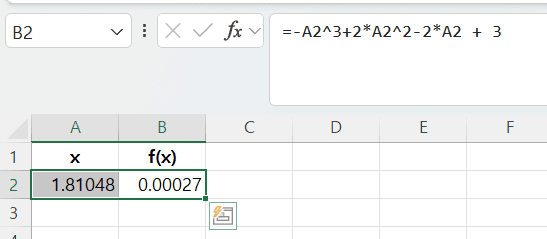
B2셀에=-A2^3+2*A2^2-2*A2+3을 입력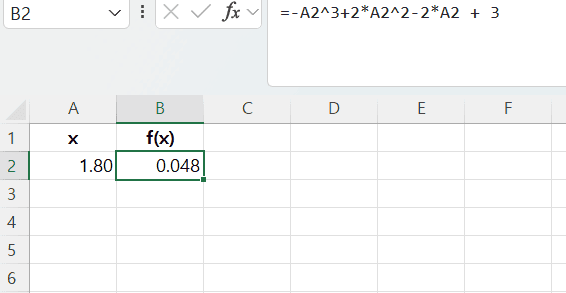
-
[데이터] 탭의 [데이터 도구]에서 [가상 분석]-[목표 값 찾기] 선택

- 목표 값 찾기 대화 상자 화면에서 다음 정보를 입력
- 수식 셀(E)
- 함수 식이 입력된 셀 (
B2)
- 함수 식이 입력된 셀 (
- 찾는 값(V)
- 목표하는 함수 값 (
0)
- 목표하는 함수 값 (
- 값을 바꿀 셀(V)
-
해를 찾기 위해 변경할 셀 (
A2)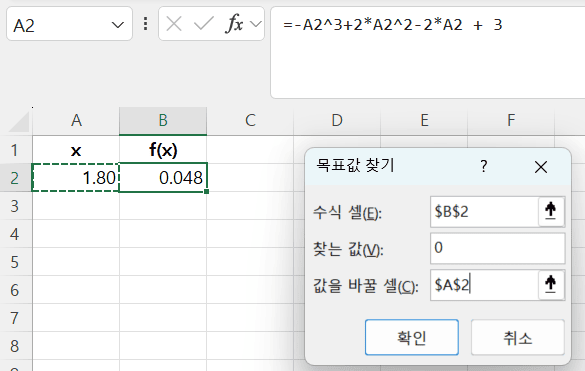
-
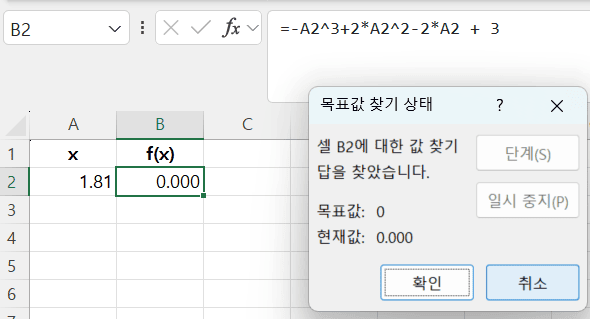
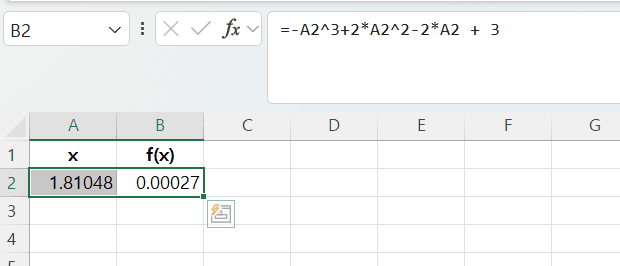
- 수식 셀(E)
-
구하고자 하는 해는 1.8105임을 알 수 있음
적분 계산
엑셀을 활용한 적분 값 계산 1
-
엑셀을 이용하여 함수의 정적분 값을 근사적으로 계산할 수 있음
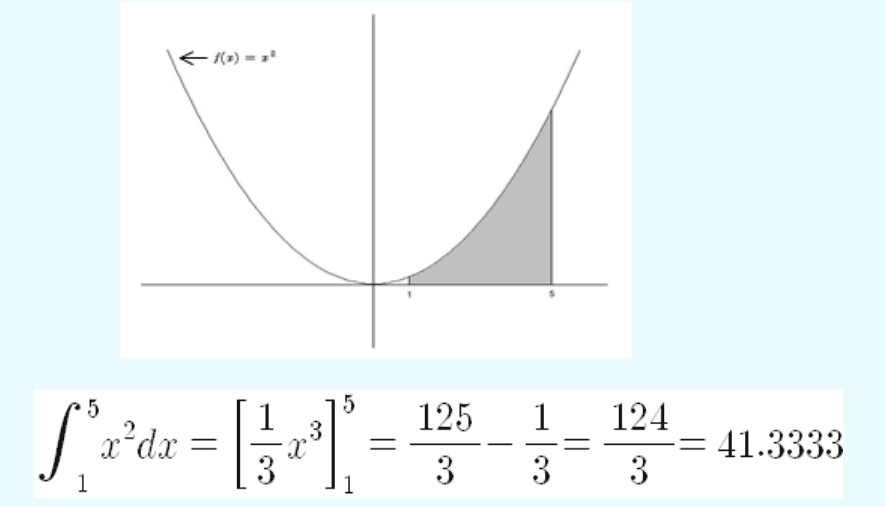
- 주로 구분구적법 또는 사다리꼴 공식의 원리를 이용
근사 적분 값 계산 2
- 먼저 구간 [a, b]를 n개로 등분함
- 각 부분의 밑변의 길이는 n / b - a 으로 동일
- 분할 된 n 개의 직사각형 넓이를 왼쪽부터 S₁, S₂, …, Sₙ 으로 표시
- Sₖ = 2 / f(xₖ ₋ ₁) + f(xₖ) * ∆x (직사각형 넓이 = 밑변 길이 * 높이)
- 여기서, ∆x = n / b - a , xₖ = a + k∆x
- S₁, S₂, …, Sₙ 을 모두 합하면 면적의 근사 값이 됨
-
n을 늘림에 따라 I = k=1 Σ n * Sₖ는 더 정확한 근사 값이 됨
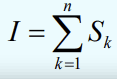
-
- 밑변의 길이 계산
- n / b - a
- ∆x = n / b - a , xₖ = a + k∆x
-
f(x), 높이, 직사각형 넓이 계산
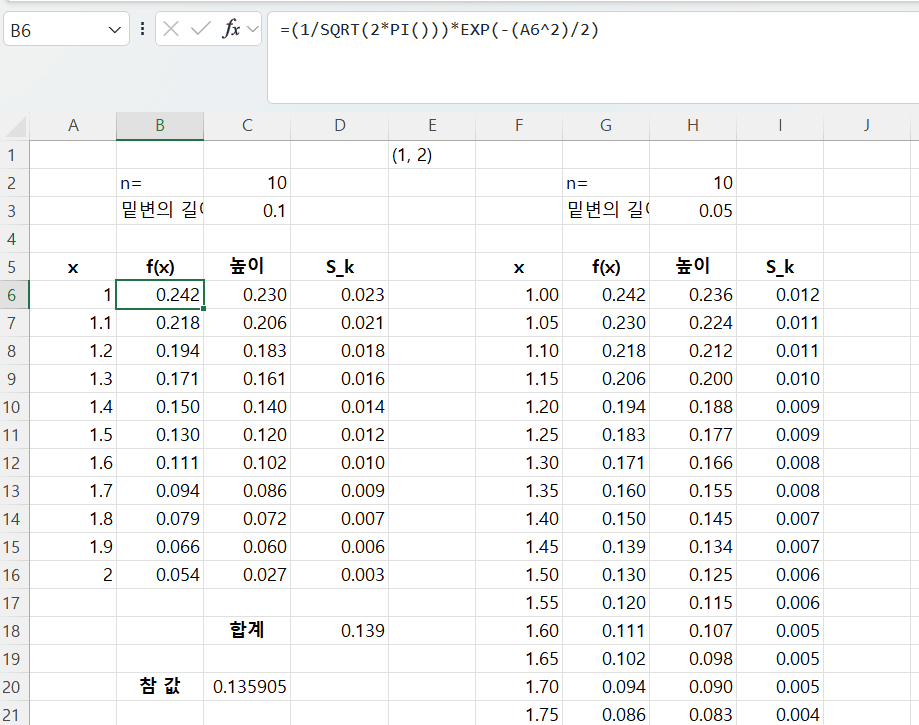
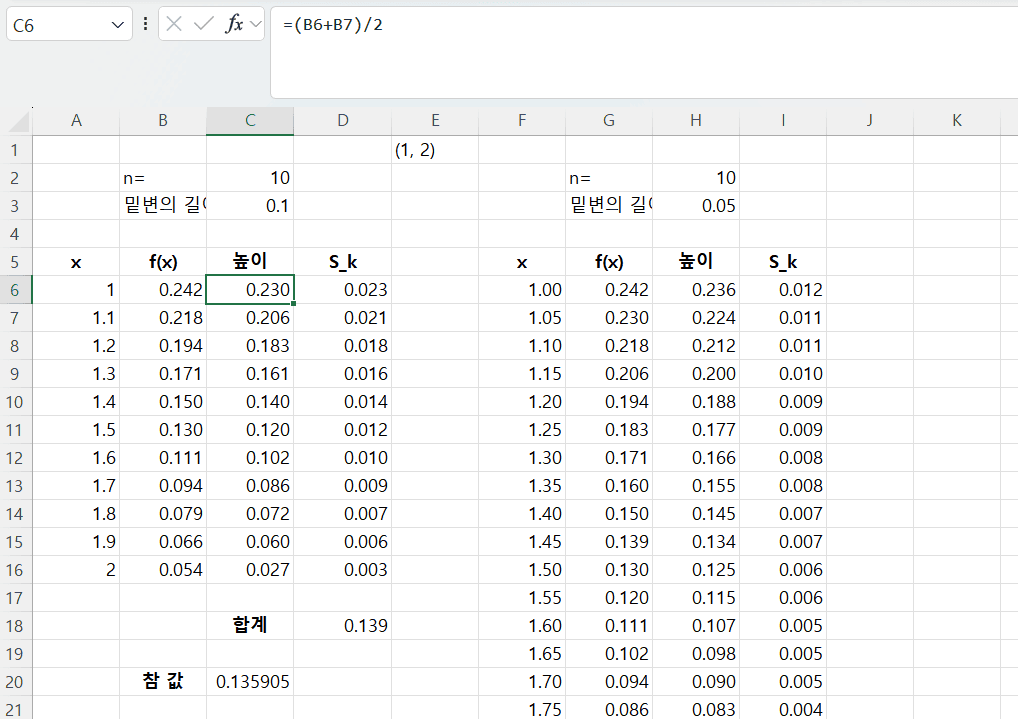
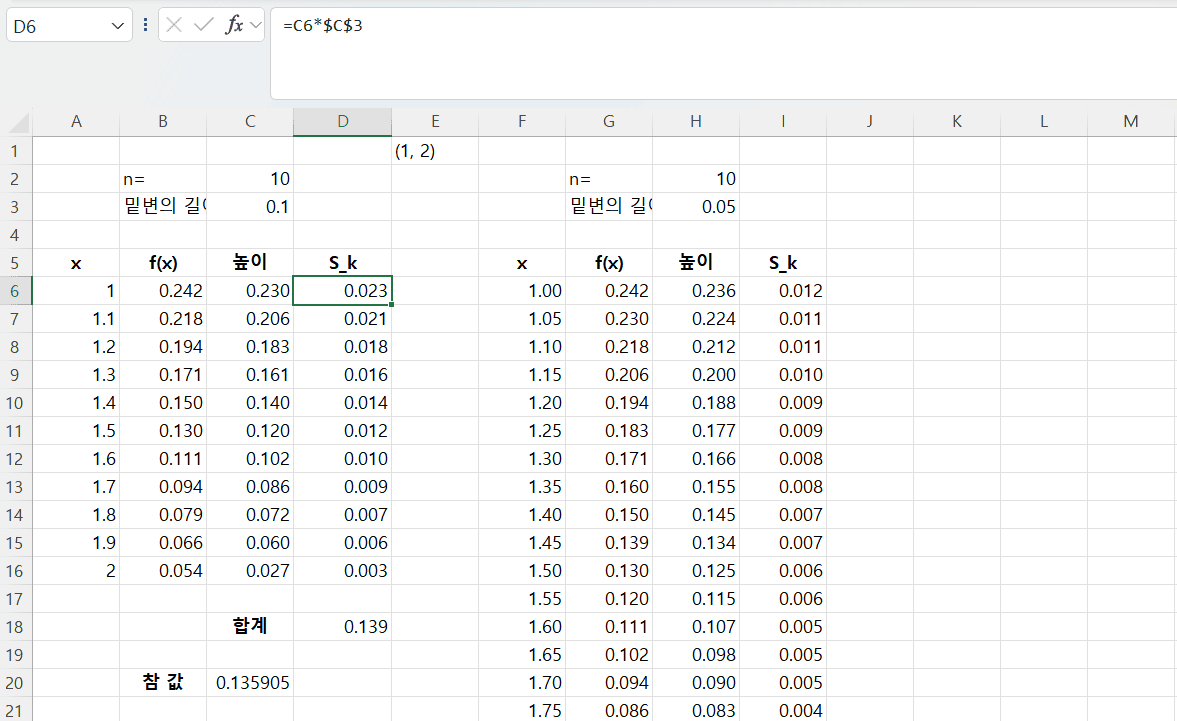
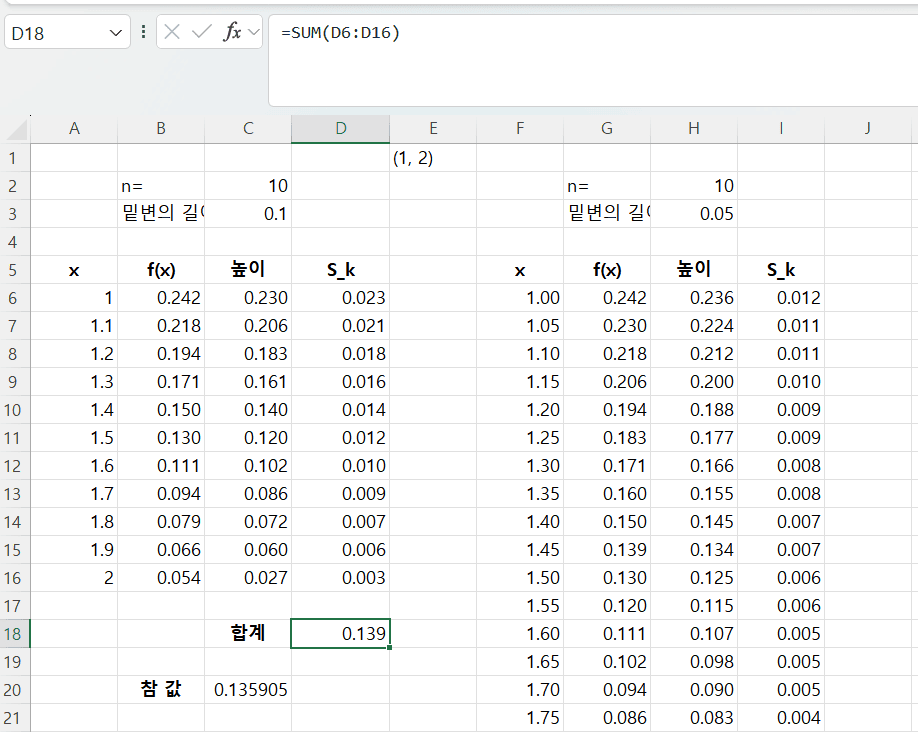
실습
-
예제 7.4 원리 합계 계산
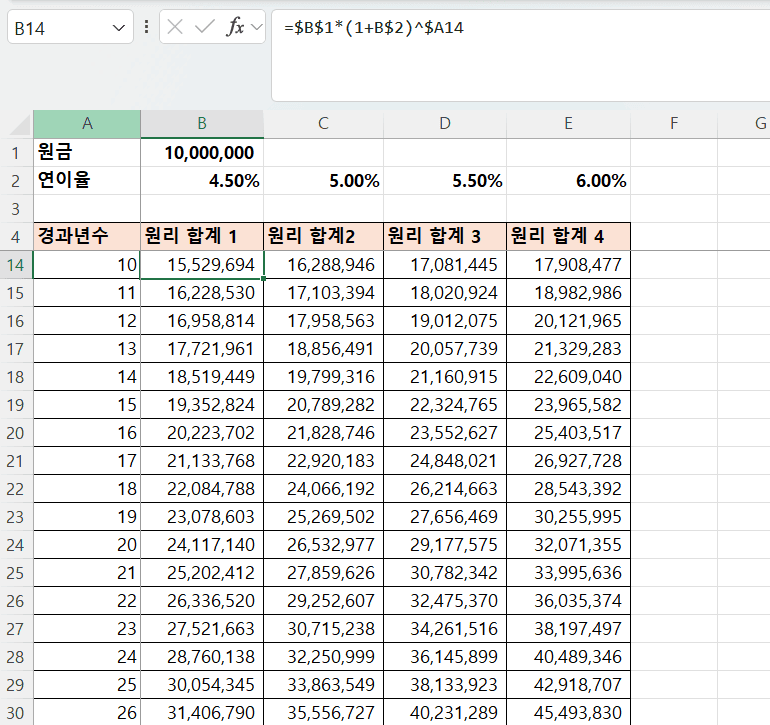
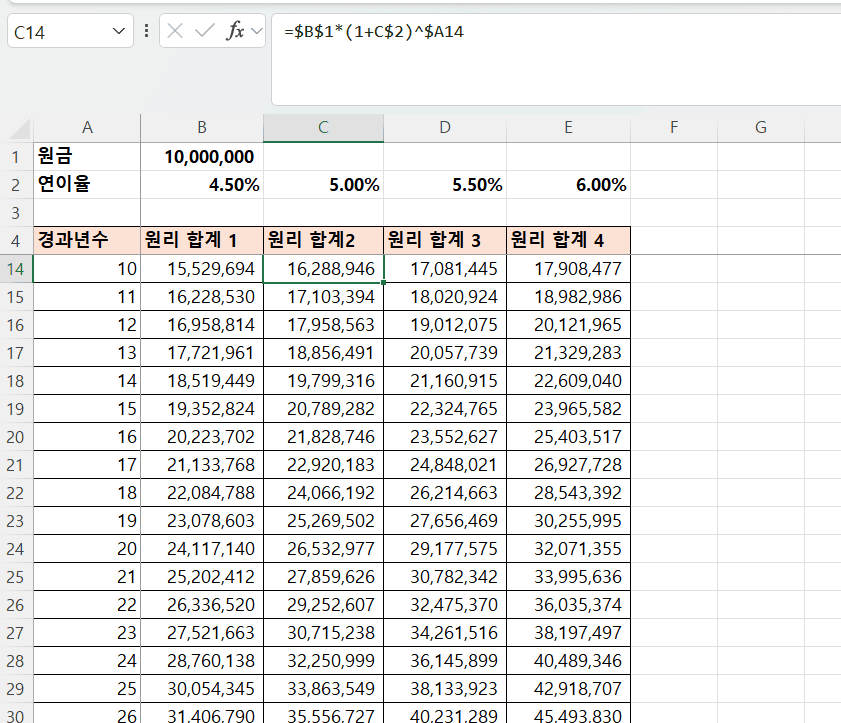
-
예제 7.5 함수 그래프 그리기, 해 찾기
-
함수 f(x) = -x^3 + 2x^2 - 2x + 3의 그래프 개형을 구간 (-3, 3)에서 그려보고, 그 구간에서 f(x) = 0 을 만족하는 근사적인 해를 엑셀을 이용해 구해보자
-
연습 문제 풀이
-
다음 정적분을 엑셀을 이용하여 계산하시오. 적분 값은 0.1359이다.
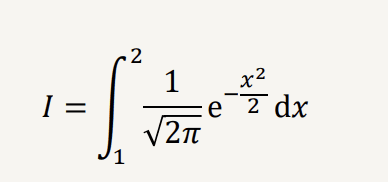
- 구간 [-3, 3] 범위에서 함수 f(x) = √2π / 1 * e^-2/x²의 그래프를 그리시오
-
구간 [1, 2]를 n = 10 등분하여 적분 값을 계산하시오 함수 식에서 π의 계산은
=PI()를 이용한다.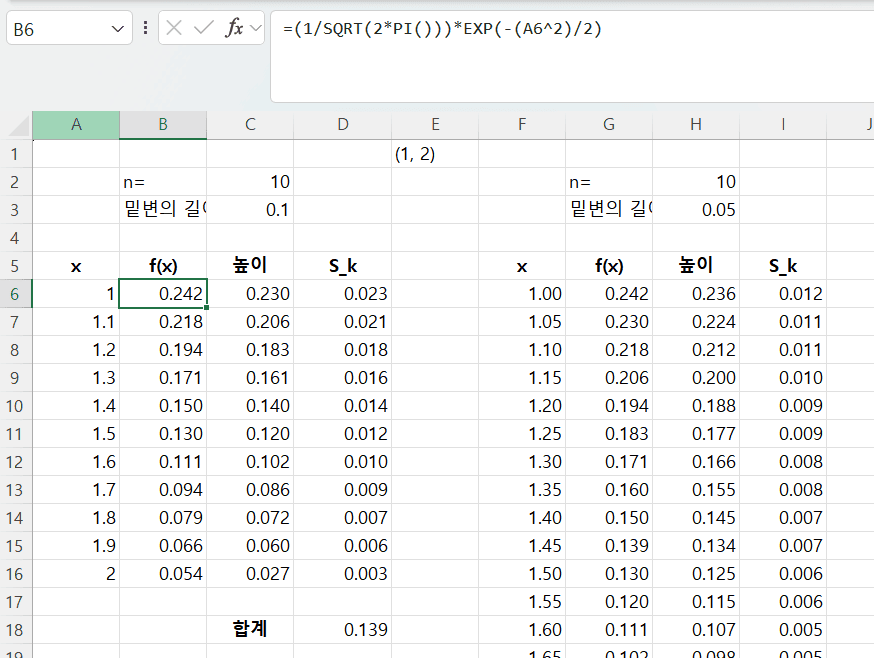
연습 문제
-
함수 f(x) = -x^3 + 2x^2 - 2x + 3의 개형을 (-3, 3) 범위에서 그리고자 한다. 차트 마법사의 차트 종류 입력 상자에서 선택할 차트 종류로 알맞은 것은?
a. 분산형
-
함수 f(x) = -x^3 + 2x^2 - 2x + 3의 개형을 (-3, 3) 범위에서 그렸더니 2 근처에서 x축을 통과한다는 것을 알았다. 엑셀을 활용하여 (-3, 3) 범위에서 -x^3 + 2x^2 - 2x + 3 = 0의 정확한 해를 구하고자 한다면 어떤 기능을 이용해야 하는가?
a. 목표 값 찾기 기능
-
다음과 같이 셀
C7에 입력되어 있는 수식을 드래그 & 드롭으로C11까지 채워서 1월부터 6월까지의 미달러($) 기준의 수출액을 원화(₩) 기준으로 바꾸고자 한다. 셀C6에 입력할 수식으로 맞는 것은?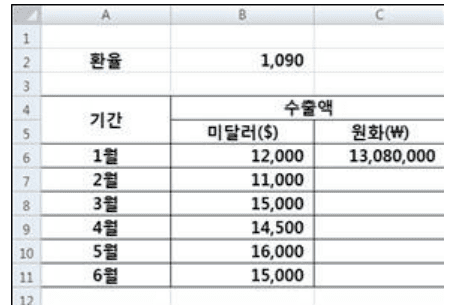
a.
=B6*B$2 -
복리로 계산 될 때 연 이율 r, 기간이 n인 경우 현재 금액 p에 대한 일정 기간 후의 원리 합계는 G = p * (1 + r)^n으로 계산할 수 있다. 원금이 1,000만원인 경우에 연 4.5%와 연 5.0%로 향후 20년까지 경과하였을 때 원리 합계가 얼마인지 계산하고자 한다. 채워 넣기를 이용하여 계산한다고 할 때
B5셀에 알맞은 함수 식은?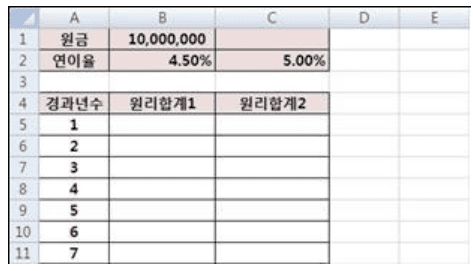
a.
=$B$1*(1+B$2)^$A5