Home [데이터 정보 처리 입문] 13강 - R을 활용한 자료 분석 2
Post
Cancel

[데이터 정보 처리 입문] 13강 - R을 활용한 자료 분석 2

Posted May 16, 2025 Updated Jul 8, 2025
By mxxikr
read 17 min

💡해당 게시글은 방송통신대학교 김성수, 이기재 교수님의 '데이터 정보 처리 입문' 강의를 개인 공부 목적으로 메모하였습니다.



학습 개요

  • R을 이용하여 데이터를 읽고, 처리하는 방법을 알아보고, 기술 통계 량을 구하는 법, 히스토그램 등 기본적인 통계 그래프를 그리는 방법을 공부함
  • Function문, 정규 분포, 이산형 및 연속형 그래프 등에 대해 알아봄



학습 목표

  • Function문 사용법을 설명할 수 있음
  • 정규 분포를 이해할 수 있음
  • 이산형 그래프를 그릴 수 있음
  • 연속형 그래프를 그릴 수 있음



강의록

Function문

Function문

  • 자주 쓰이는 계산 등은 Function문으로 작성하는 것이 좋음

  • 제곱 값을 반환하는 함수:

    1
2

      sq_value <- (function(x) { x*x })
  sq_value(4)

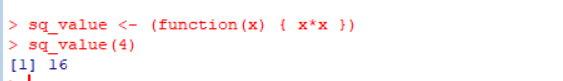
    image.png

  • power 값을 반환하는 함수

    1
2
3

      fpower <- function(x,n) {x^n}
  fpower(3, 2)
  fpower(4, 1/2)

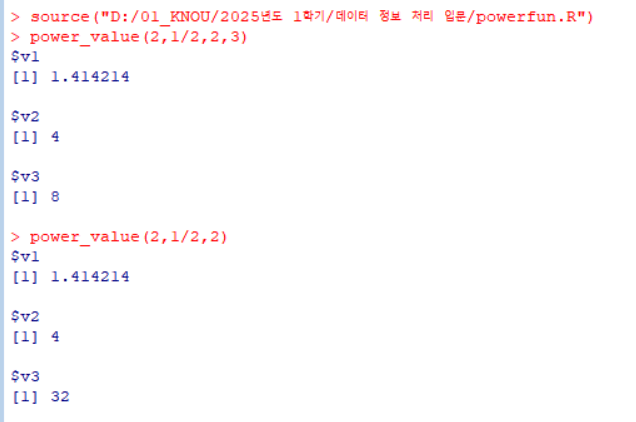
    image.png

  • 여러 개의 power 값을 동시에 반환하는 함수 : powerfun.r

    1
2
3
4
5
6
7
8
9

      power_value <- function(x, n1, n2, n3=5)
  {
    n1_val = x^n1
    n2_val = x^n2
    n3_val = x^n3
    value = list(v1=n1_val, v2=n2_val, v3=n3_val)
    return(value)
  }
    

    1
2
3

      source("D:/01_KNOU/2025년도 1학기/데이터 정보 처리 입문/powerfun.R") # 작성된 프로그램을 r에서 배치로 수행하는 방법
  power_value(2, 1/2, 2, 3)
  power_value(2, 1/2, 2)

    image.png

정규분포

정규분포 (normal distribution)

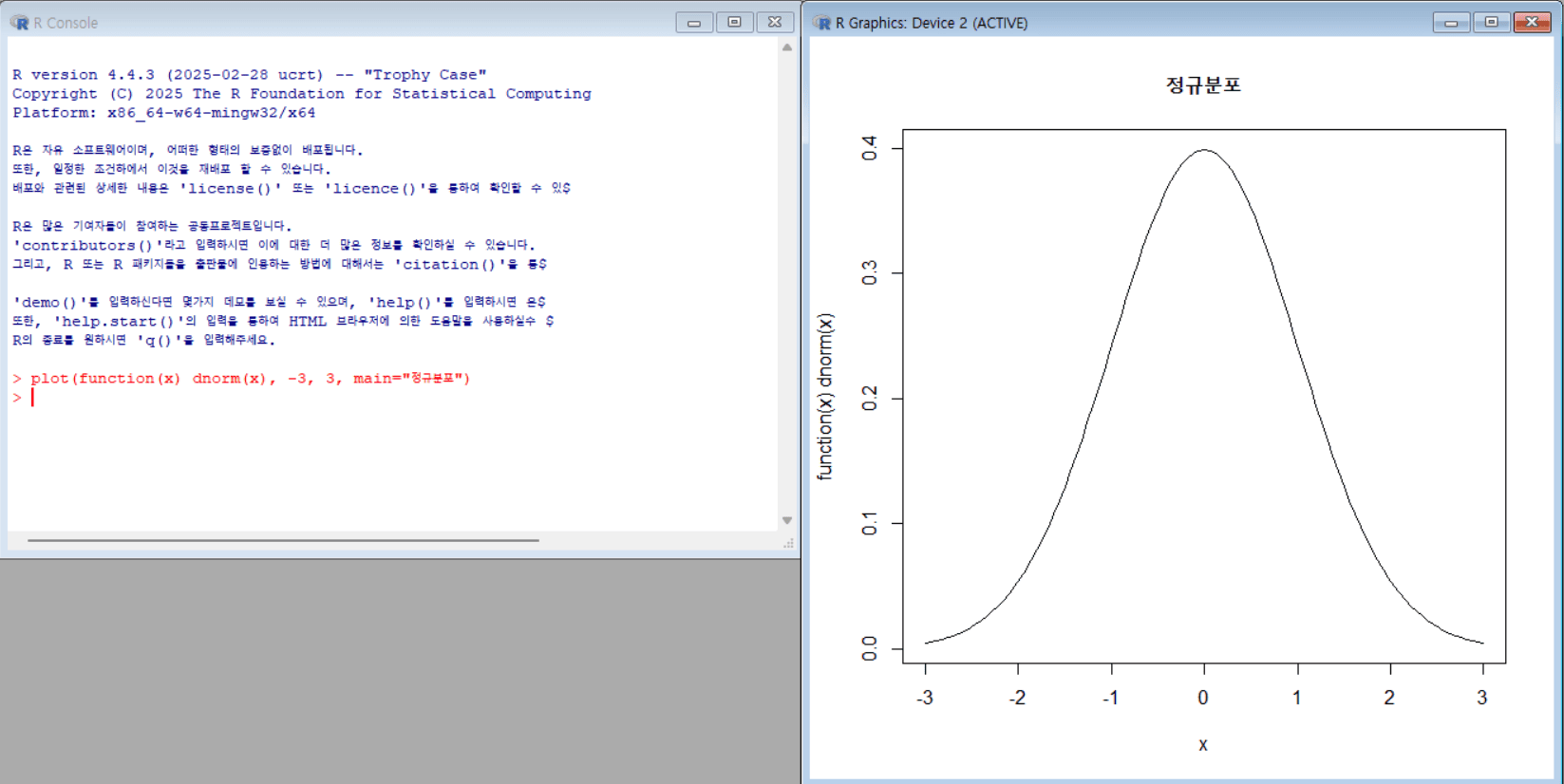
  • 정규분포 그리기

    1
2
3
4
5
6
7

      # -3부터 3까지의 구간에서 표준 정규분포(평균 0, 표준편차 1)의 확률밀도함수 그래프를 그림
  plot(
    function(x) dnorm(x), # x값에 대해 표준 정규분포의 밀도 값을 계산하는 함수
    -3,                   # x축의 최소값
    3,                    # x축의 최대값
    main = "정규분포"     # 그래프 제목을 정규분포로 설정
  )

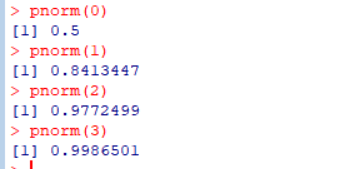
    image.png

  • Pr(X ≤ x) 구하기

    1
2
3
4

      pnorm(0) # 표준 정규분포에서 0 이하일 확률을 구하는 함수
  pnorm(1) # 표준 정규분포에서 1 이하일 확률을 구하는 함수
  pnorm(2) # 표준 정규분포에서 2 이하일 확률을 구하는 함수
  pnorm(3) # 표준 정규분포에서 3 이하일 확률을 구하는 함수

    image.png

정규 분포 난수(random number) 생성

  • 정규 분포를 따르는 난수 생성
    • rnorm 함수 이용

  • 평균이 0, 표준 편차가 1인 정규 분포를 따르는 난수 20개 생성

    1

      rnorm(20) # 표준 정규분포에서 난수 20개 생성

    image.png

  • 평균이 -5이고, 표준 편차가 2.5인 정규분포를 따르는 난수 100개 생성

    1

      rnorm(100, -5, 2.5) # 평균이 -5, 표준편차가 2.5인 정규분포에서 난수 100개 생성

    image.png

  • 난수 생성 후 평균, 표준 편차 확인 및 히스토그램 그리기

    1
2
3
4

      ran_norm = rnorm(100) # 표준 정규분포에서 난수 100개를 생성하여 ran_norm에 저장
  mean(ran_norm)        # ran_norm 값들의 평균값 계산
  sd(ran_norm)          # ran_norm 값들의 표준편차 계산
  hist(ran_norm)        # ran_norm 값들에 대한 히스토그램(분포도) 생성

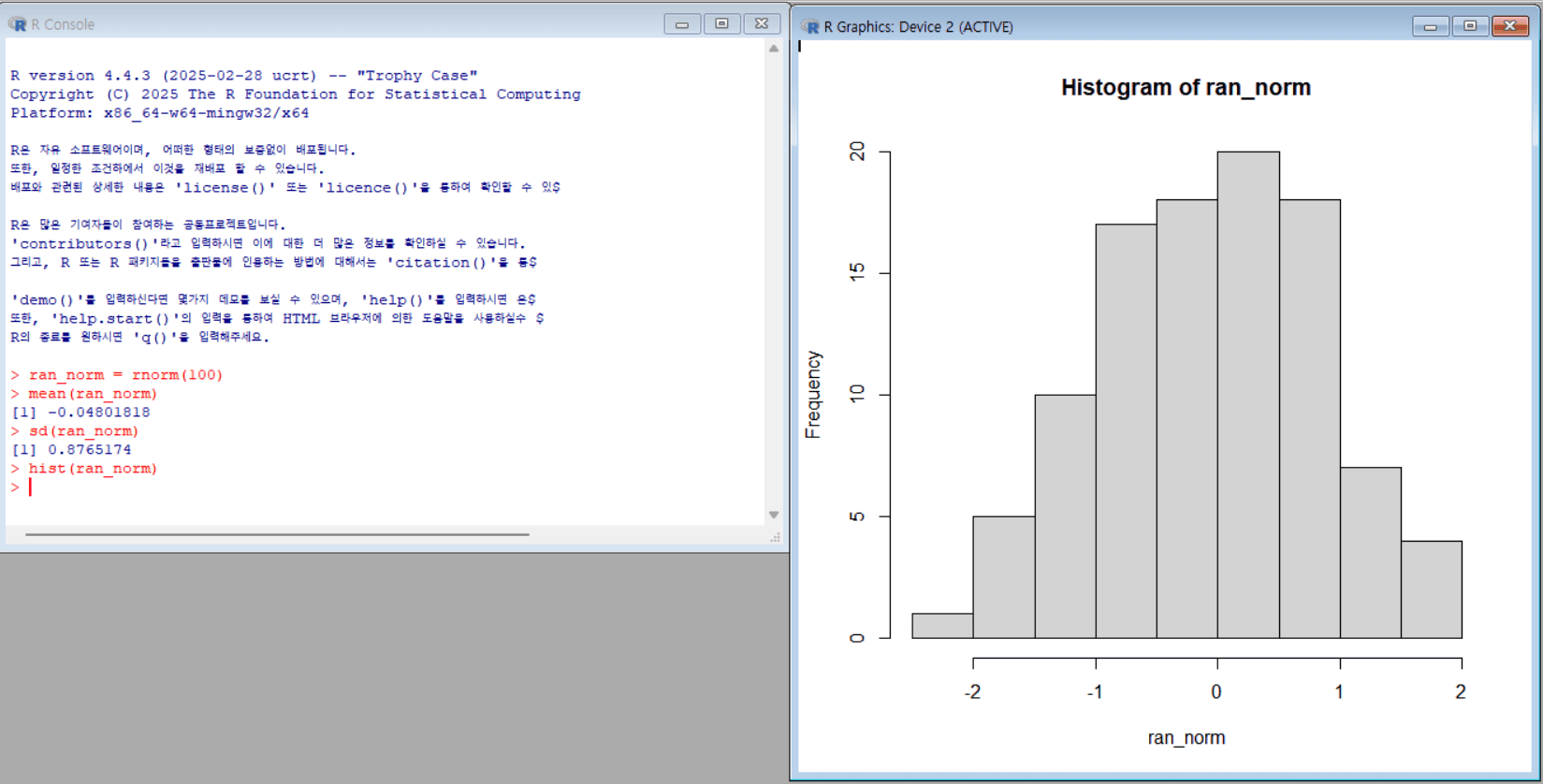
    image.png

이산형 그래프 그리기

예제 1

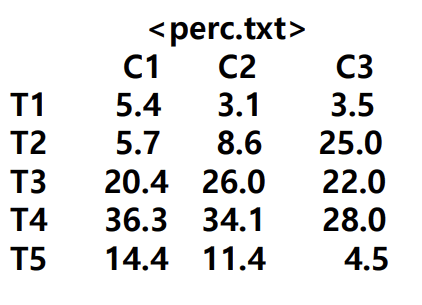
  • 세 그룹(C1, C2, C3)이 다섯 자선단체(T1,…,T5)에 기부하는 다음 가상 자료를 이용하여 막대 그림, 원 그림을 그려보자

    image.png

막대 그림 그리기

  • 데이터 읽기

    1
2
3
4

      percData <- read.table("D:/01_KNOU/2025년도 1학기/데이터 정보 처리 입문/dataintro/perc.txt", header=T) # perc.txt 파일을 데이터프레임으로 불러오기, 첫 행을 변수명으로 사용
  percData <- as.matrix(percData) # 데이터프레임을 행렬로 변환
  var_name <- colnames(percData)  # 열(변수)이름을 var_name 변수에 저장
  case_name <- rownames(percData) # 행(케이스)이름을 case_name 변수에 저장

  • 막대 그림 그리기

    1
2
3
4

      # barplot
  barplot(percData, names=var_name) # percData 행렬을 막대그래프로 그림. x축 이름은 var_name 사용
  legend(locator(1), case_name)     # 그래프에서 클릭한 위치에 범례 추가, 범례 이름은 case_name
  title("Barplot")                  # 그래프 제목을 "Barplot"으로 설정

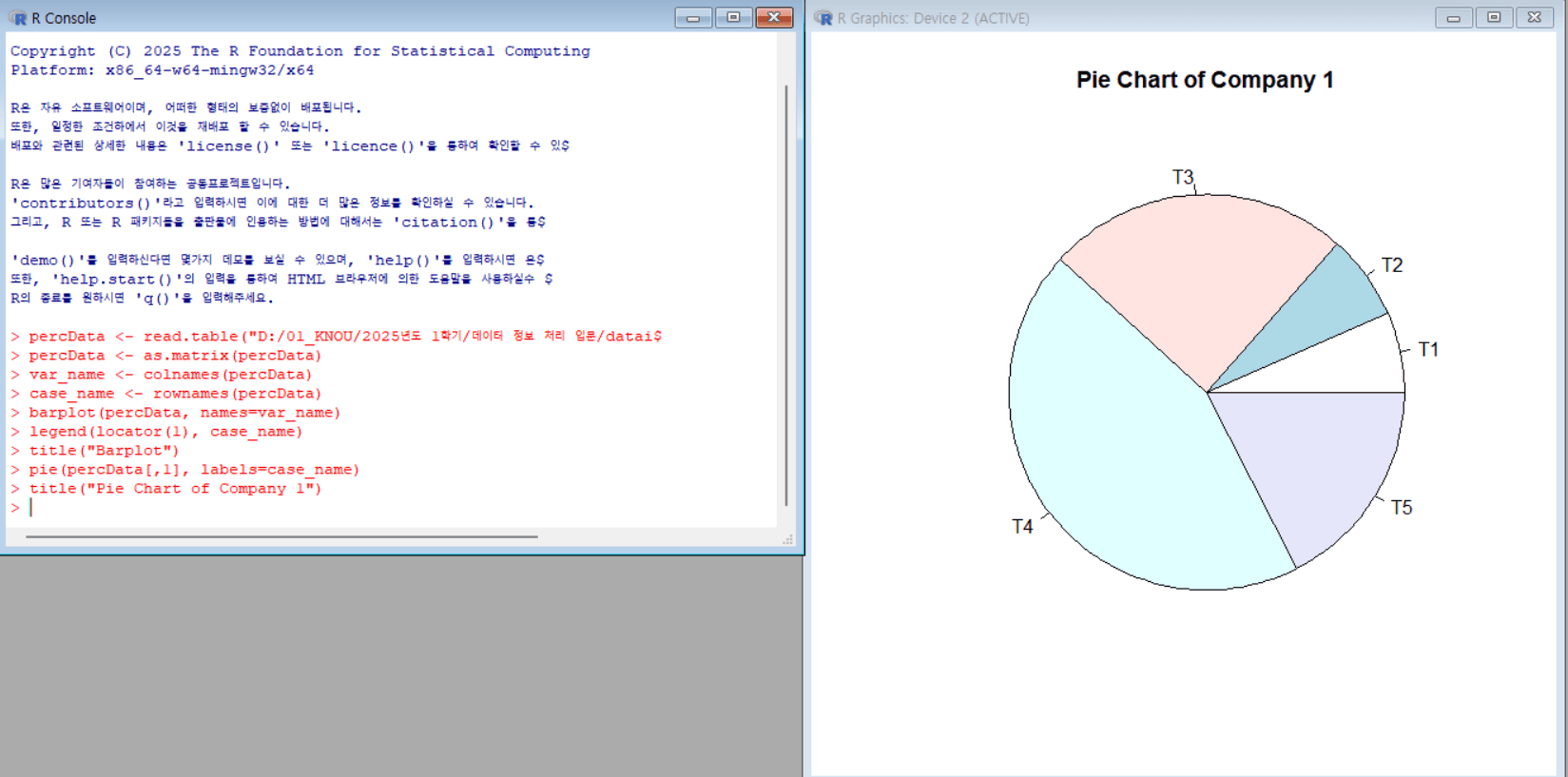
    image.png

원 그림 그리기

  • 원 그림 그리기

    1
2
3

      # Piechart
  pie(percData[,1], labels=case_name) # percData의 첫 번째 열의 값을 케이스별로 파이차트로 그림, 라벨은 case_name 사용
  title("Pie Chart of Company 1") # 그래프 제목을 "Pie Chart of Company 1"으로 설정

    image.png

예제 2

  • 한 설문조사에서 다음 6개 문항에 대하여 표본 추출 된 40명을 대상으로 조사한 자료이다. R을 이용하여 교육 정도에 대한 수직형 막대 그림을 그려라. 또 각각의 성별(남자, 여자)에 대하여 교육 정도에 대한 수직형 막대그림을 그려라.

    image.png

    image.png

막대 그림 그리기

1
2
3
4
5
6
7
8
9
10

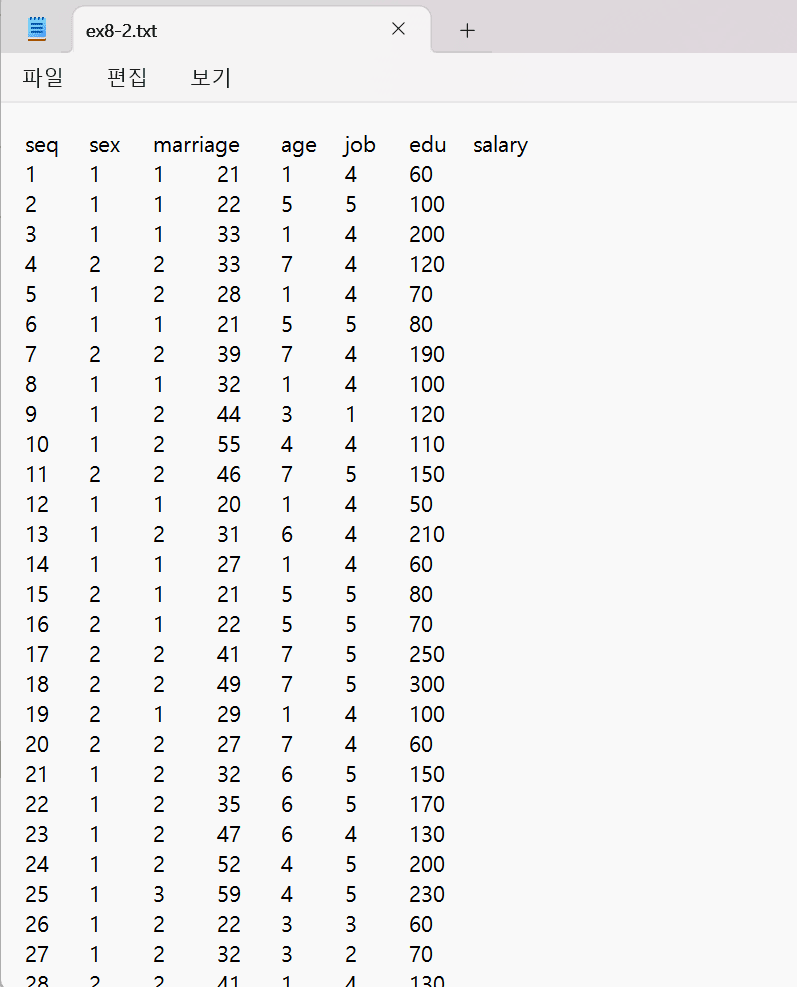
ex8_2 = read.csv("D:/01_KNOU/2025년도 1학기/데이터 정보 처리 입문/dataintro/ex8-2.csv") # ex8-2.csv 파일을 읽어와 ex8_2 데이터프레임에 저장
colnames(ex8_2) # 데이터프레임의 열(변수)이름을 확인

edu_tb = table(ex8_2$edu) # ex8_2 데이터프레임의 edu' 변수의 각 값에 대한 빈도표(도수분포표)를 생성하여 edu_tb에 저장
edu_tb  # 생성된 도수분포표를 확인

rownames(edu_tb) = c("무학", "초졸", "중졸", "고졸", "대졸") # 각 도수에 해당하는 교육단계별 이름을 부여
edu_tb  # 이름이 부여된 도수분포표를 다시 확인

barplot(edu_tb) # 교육단계별 빈도를 막대그래프로 시각화

image.png

성별 구분 막대 그림 그리기

1
2
3
4
5
6
7
8
9

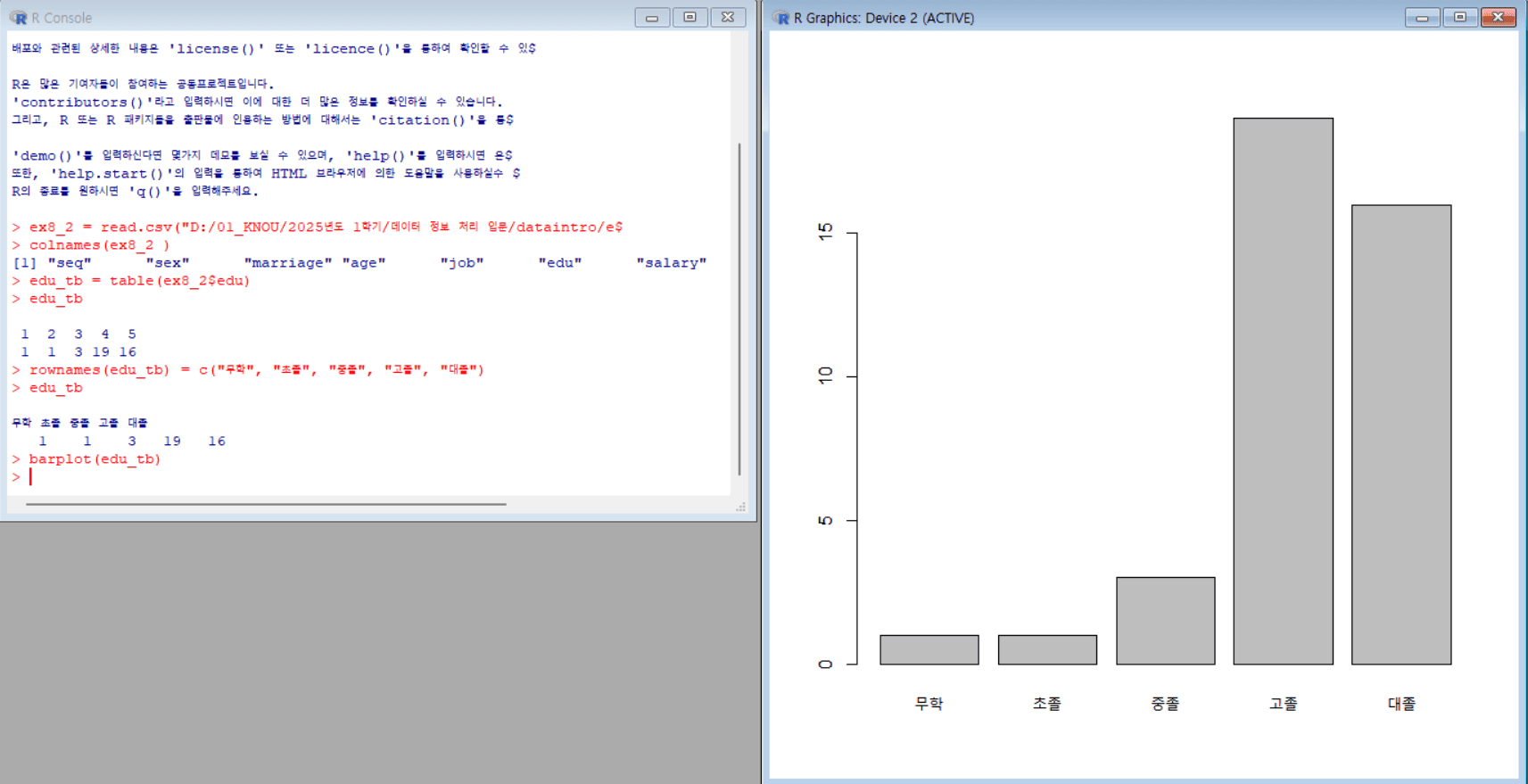
EduSex = list(ex8_2$sex, ex8_2$edu)      # sex와 edu 데이터를 리스트로 묶음
EduSex_tb = table(EduSex)                # 두 범주형 변수(sex, edu)로 교차표(도수분포표)를 생성
EduSex_tb                                # 생성된 교차표 확인

colnames(EduSex_tb) = c("무학", "초졸", "중졸", "고졸", "대졸") # 열이름을 한글로 지정
rownames(EduSex_tb) = c("남성", "여성")                        # 행이름을 한글로 지정
EduSex_tb                                   # 한글 라벨이 적용된 교차표 확인

barplot(EduSex_tb) # sex와 edu에 대한 누적 막대그래프를 그림

image.png

성별 구분 원 그림 그리기

1
2
3
4
5
6

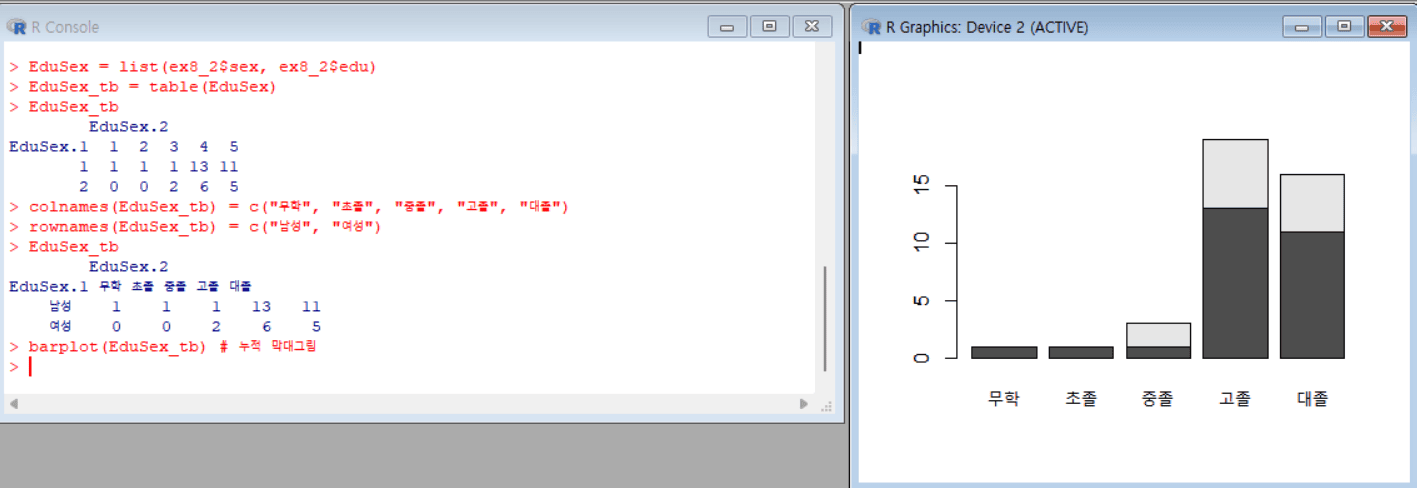
# Piechart
par(mfrow=c(1,2)) # 그래프 영역 분할
pie(EduSex_tb[1,]) # 남성 교육 정도 원그림
title("Education of Male")
pie(EduSex_tb[2,]) # 여성 교육 정도 원그림
title("Education of Female")

image.png

연속형 그래프 그리기

상자 그림

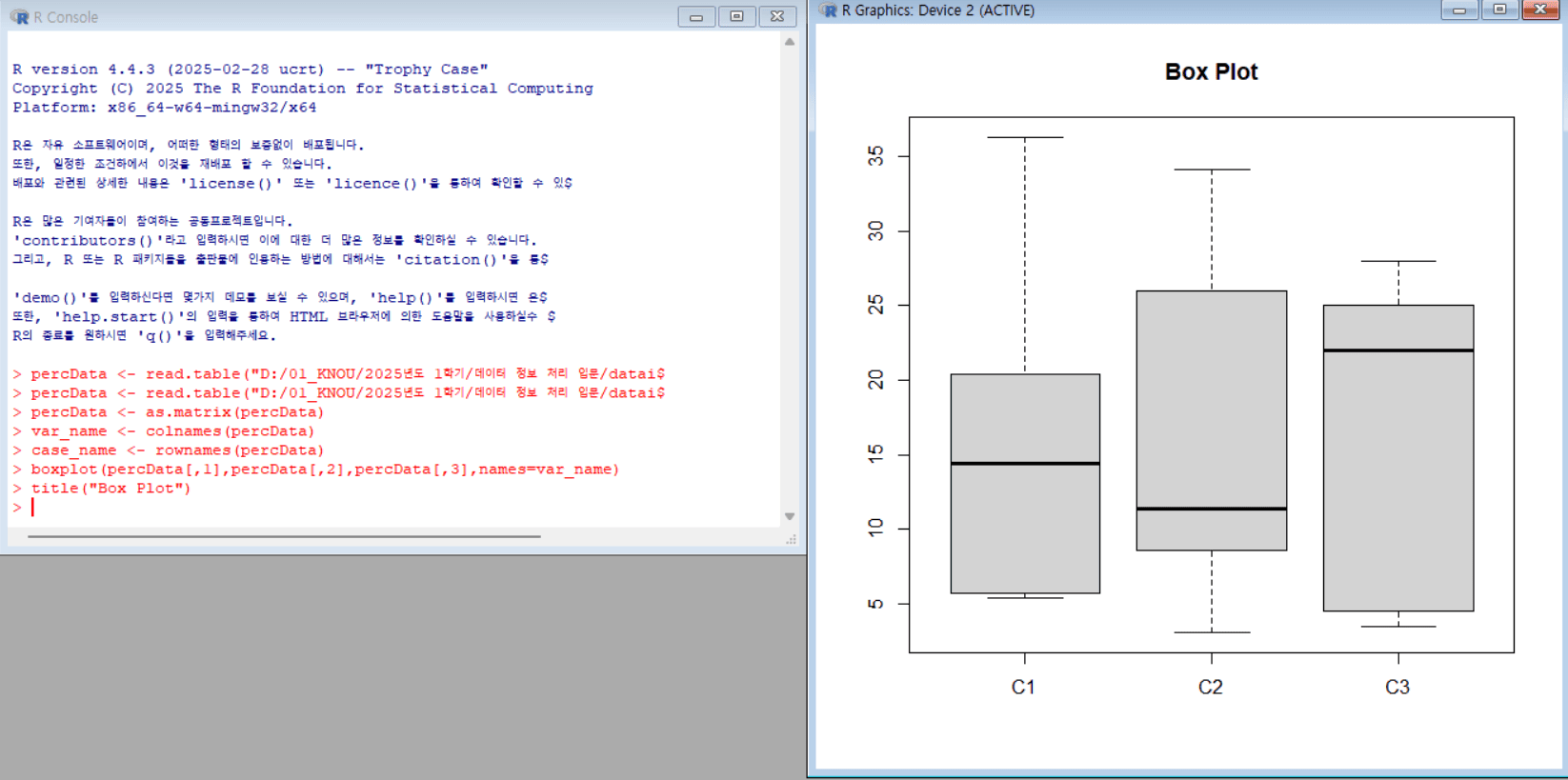
  • percData의 세 회사(C1, C2, C3) 상자 그림 그리기

    1
2
3
4

      percData <- read.table("D:/01_KNOU/2025년도 1학기/데이터 정보 처리 입문/dataintro/perc.txt", header=T)
  percData <- as.matrix(percData)
  var_name <- colnames(percData)
  case_name <- rownames(percData)

    1
2

      boxplot(percData[,1], percData[,2], percData[,3], names=var_name) # percData의 세 열에 대해 상자 그림을 그림. 각 boxplot의 이름은 var_name 사용
  title("Box Plot") # 그래프 제목을 Box Plot으로 설정

    image.png

줄기-잎 그림 및 히스토그램

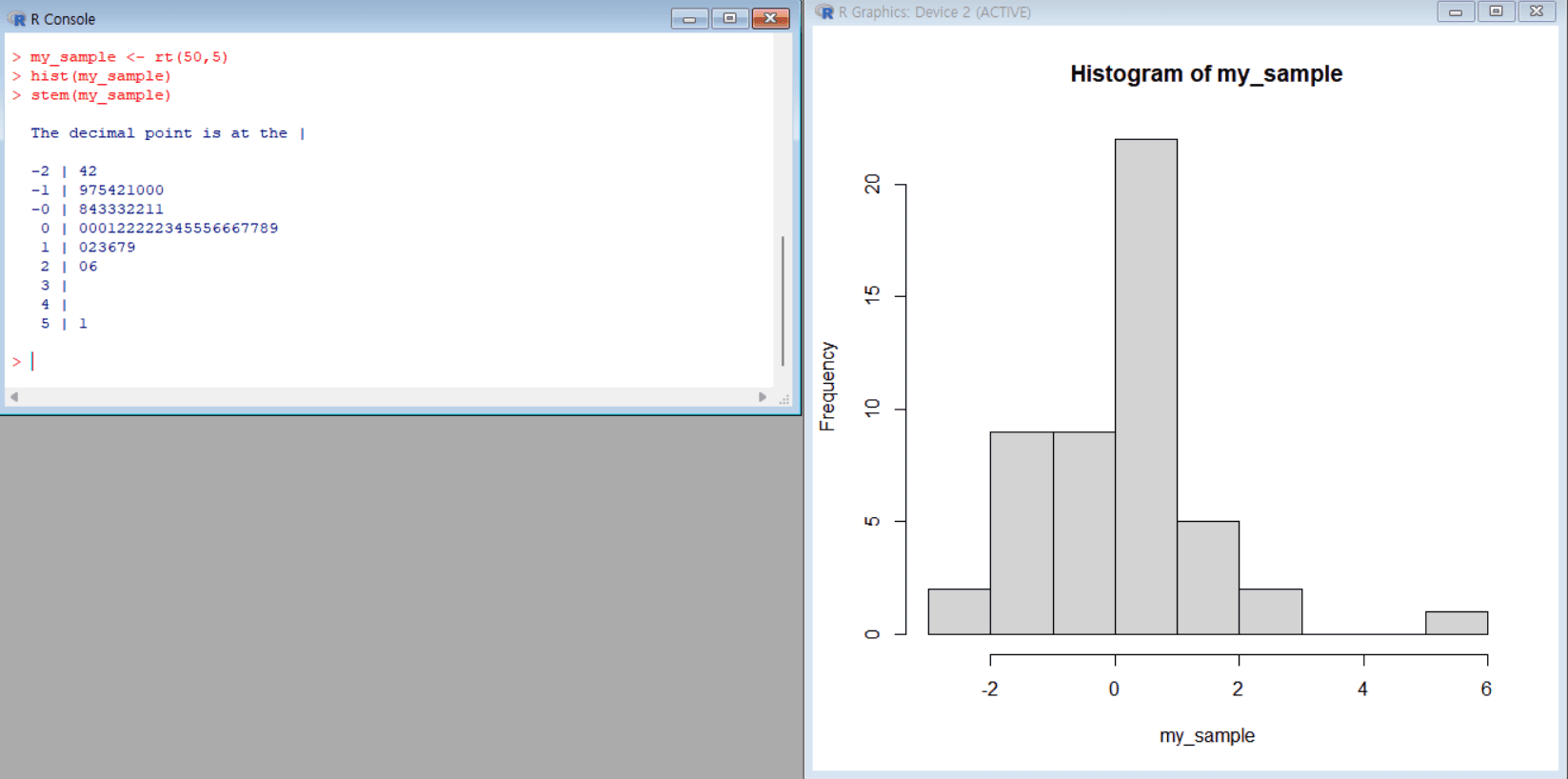
  • 자유도가 5인 t-분포를 따르는 난수 50개를 만들어 히스토그램 및 줄기-잎 그림 그리기

    1
2
3

      my_sample <- rt(50, 5)     # 자유도 5인 t-분포에서 임의로 50개의 샘플을 생성하여 my_sample에 저장
  hist(my_sample)            # 생성된 샘플(my_sample)에 대한 히스토그램을 그림 -> 데이터의 분포를 시각적으로 확인
  stem(my_sample)            # 생성된 샘플(my_sample)에 대한 줄기-잎 그림을 출력 -> 데이터의 분포와 개별 값들을 세밀하게 확인

    image.png

시계 열 그림

  • R 시스템에 내장된 데이터 co2를 이용한 시계열 그림 그리기

    1
2
3

      co2                            # 내장된 월별 대기 중 CO2 농도(time series 데이터) 출력
  plot(co2)                      # co2 데이터를 시계열(time series) 그래프로 그림
  lines(smooth(co2), col="BLUE") # co2 데이터에 스무딩 처리를 한 선을 파란색으로 그래프 위에 추가

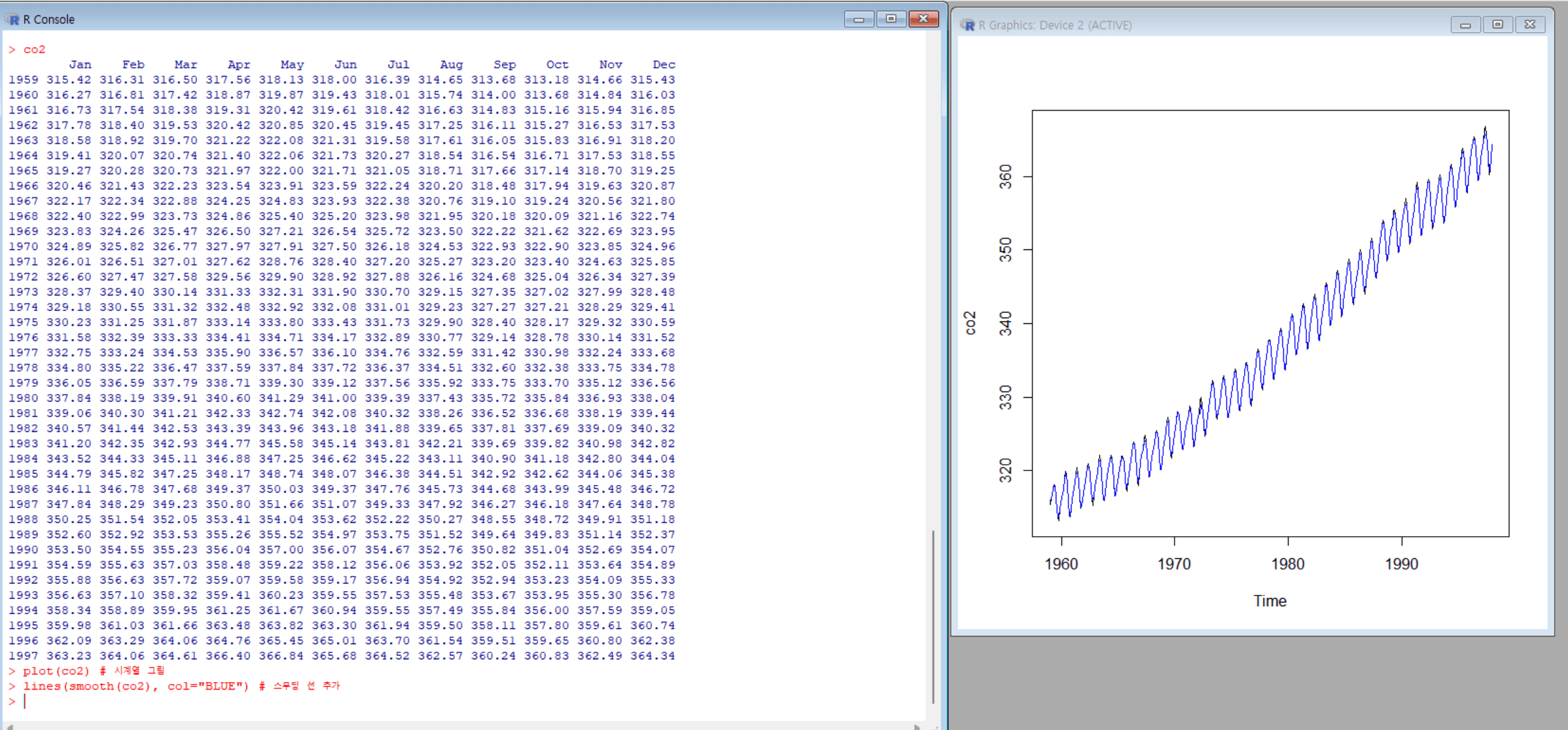
    image.png

    • smooth() 함수
      • 이동 평균 등의 방식으로 데이터를 부드럽게 처리
    • lines()
      • 원본 데이터 위에 스무딩된 선을 덧그림

함수 그리기

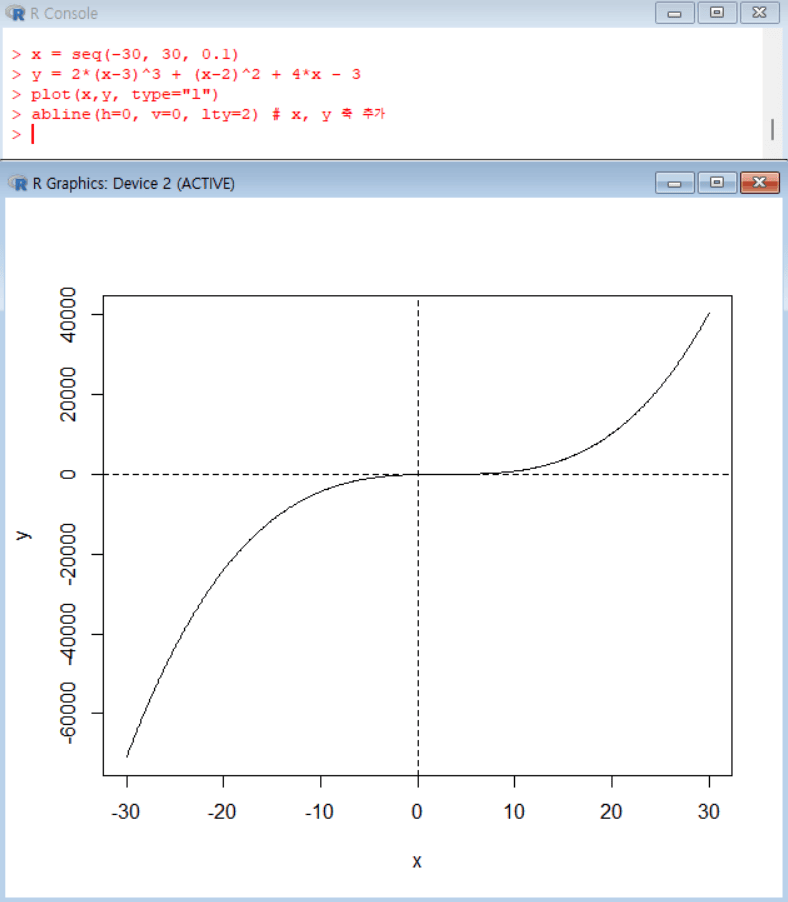
  • 수학 함수 그래프 그리기

    1
2
3
4

      x = seq(-30, 30, 0.1)             # -30부터 30까지 0.1 간격으로 x값을 생성
  y = 2*(x-3)^3 + (x-2)^2 + 4*x - 3 # y = 2(x-3)^3 + (x-2)^2 + 4x - 3 함수를 x의 값에 따라 계산
  plot(x, y, type="l")              # (x, y) 좌표를 선(line) 그래프로 그림
  abline(h=0, v=0, lty=2)           # y=0(수평축), x=0(수직축)을 점선(linetype=2)으로 추가

    image.png

히스토그램 그리기

  • 예제2 자료에서 변수 age 히스토그램 그리기

    1
2
3
4
5
6

      ex8_2 = read.csv("D:/01_KNOU/2025년도 1학기/데이터 정보 처리 입문/dataintro/ex8-2.csv") # 지정한 경로의 CSV 파일에서 데이터를 읽어와 ex8_2라는 데이터프레임에 저장함
  ageHist = hist(ex8_2$age, col="BLUE")  # ex8_2 데이터의 age 변수로 파란색 히스토그램 그리고 결과 객체를 ageHist에 저장
  names(ageHist)                         # 히스토그램 객체(ageHist)의 구성 요소 이름을 확인
  ageHist$breaks                         # 히스토그램의 구간(계급)의 경계값(벡터) 확인
  ageHist$counts                         # 각 구간(계급)별 데이터 개수(도수) 확인
  ageHist$mids                           # 각 구간(계급)의 중앙값 확인

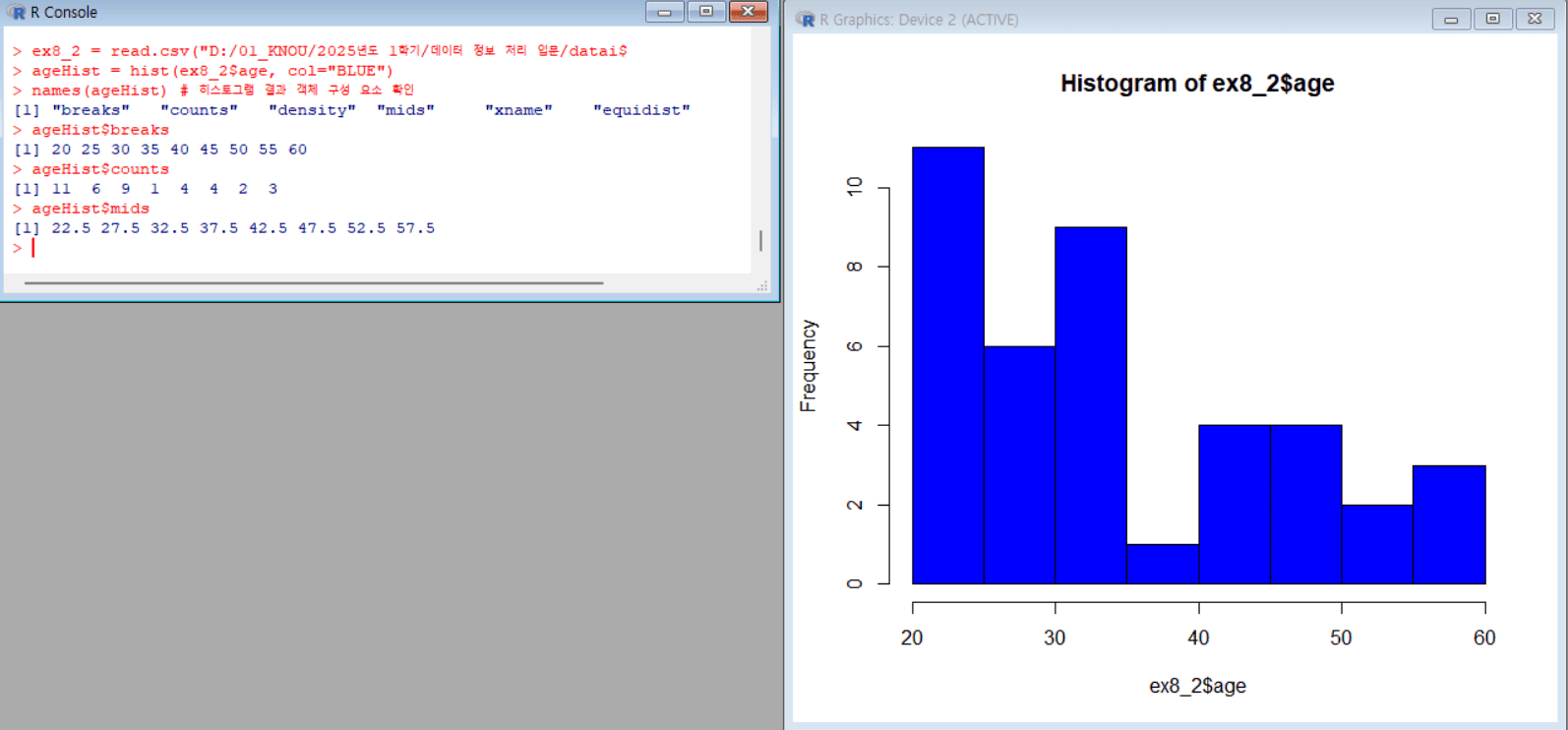
    image.png

그룹별 줄기-잎 그림 그리기

  • 예제2 자료에서 남녀(sex)별로 변수 age 줄기-잎 그림 그리기

    1
2
3
4
5
6
7
8
9

      stem(ex8_2$age[ex8_2$sex==1])  # 성별이 1인 사람들의 나이에 대한 줄기-잎 그림 출력
  stem(ex8_2$age[ex8_2$sex==2])  # 성별이 2인 사람들의 나이에 대한 줄기-잎 그림 출력
    
  library(aplpack)               # stem.leaf.backback 함수를 사용하기 위해 aplpack 패키지 로드
    
  m_age = ex8_2$age[ex8_2$sex==1] # 남성(male)의 나이 데이터 벡터 생성
  f_age = ex8_2$age[ex8_2$sex==2] # 여성(female)의 나이 데이터 벡터 생성
    
  stem.leaf.backback(m_age, f_age) # 남성과 여성의 나이 분포를 비교하는 back-to-back(양방향) 줄기-잎 그림 출력

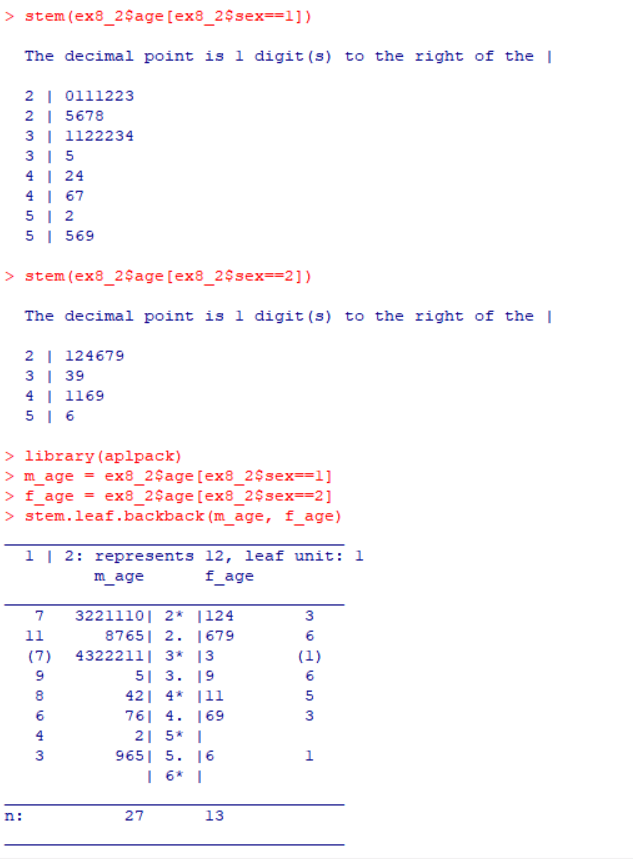
    image.png

그룹별 상자 그림 그리기

  • 그룹별 상자 그림 그리기

    1

      boxplot(age ~ sex, data=ex8_2) # # ex8_2 데이터에서 sex에 따라 age의 분포를 상자 그림으로 그림

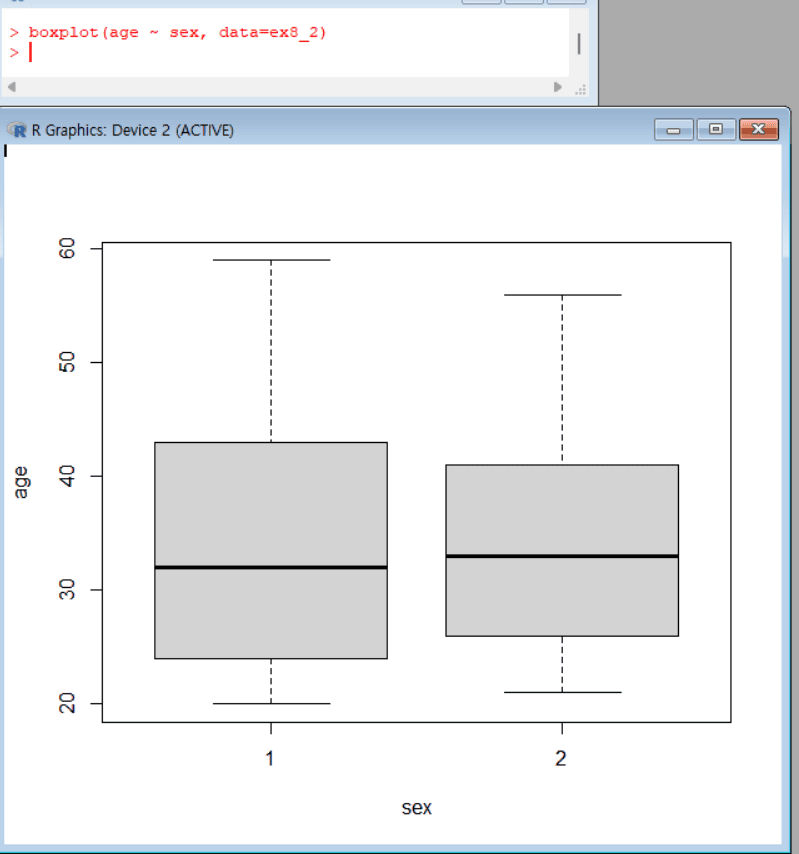
    image.png

    • 각 상자는 해당 sex 그룹의 age 분포(최소값, 1사분위수, 중앙값, 3사분위수, 최대값 등)를 시각적으로 나타냄

그룹 구분 산점도 그리기

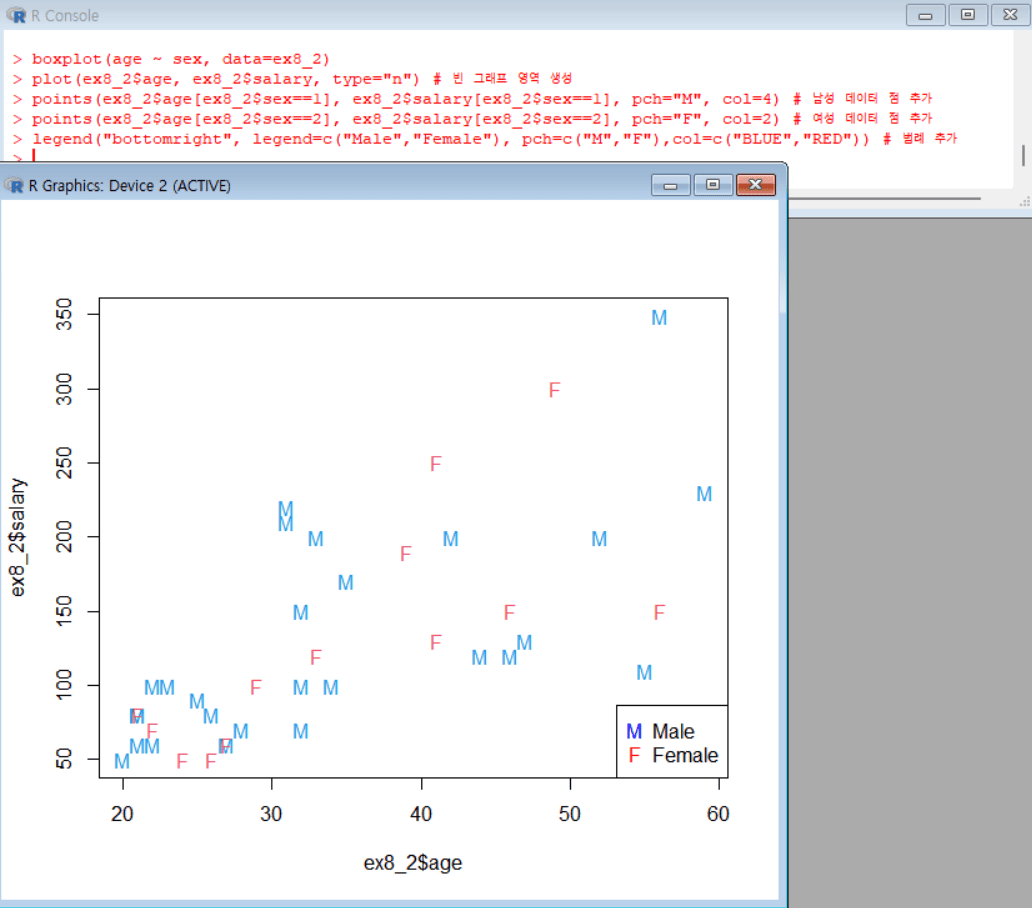
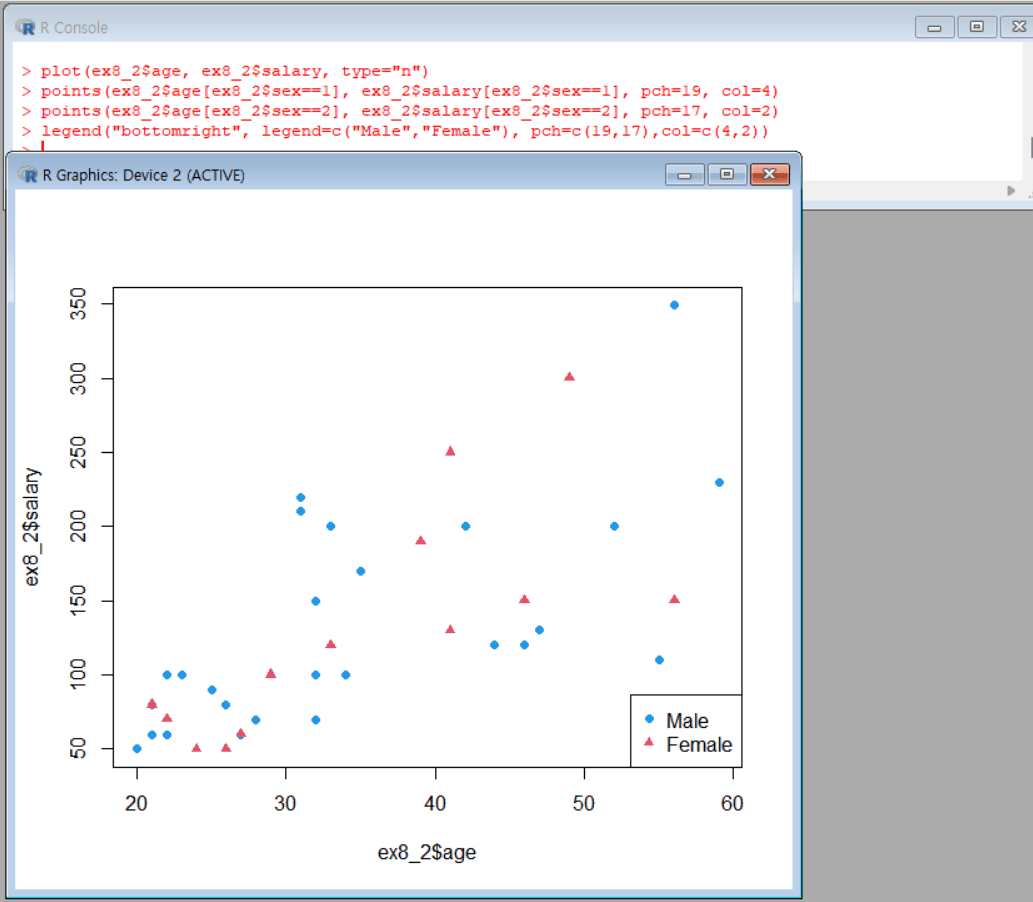
  • 예제2 자료에서 남녀(sex)별로 구분한 (나이, 월수입) 산점도 그리기

    1
2
3
4

      plot(ex8_2$age, ex8_2$salary, type="n") # 빈 그래프 영역 생성
  points(ex8_2$age[ex8_2$sex==1], ex8_2$salary[ex8_2$sex==1], pch="M", col=4) # 남성 데이터 점 추가
  points(ex8_2$age[ex8_2$sex==2], ex8_2$salary[ex8_2$sex==2], pch="F", col=2) # 여성 데이터 점 추가
  legend("bottomright", legend=c("Male","Female"), pch=c("M","F"),col=c("BLUE","RED")) # 범례 추가

    image.png

    1
2
3
4
5
6
7
8
9
10
11

      plot(ex8_2$age, ex8_2$salary, type="n") 
  # 전체 데이터에서 age를 x축, salary을 y축으로 사용하여 좌표 평면만 생성함 (type="n"은 점이나 선을 그리지 않고 빈 그래프만 만듦)
    
  points(ex8_2$age[ex8_2$sex==1], ex8_2$salary[ex8_2$sex==1], pch=19, col=4)
  # sex가 1인 사람들의 age와 salary 데이터를 파란색(col=4) 원형 점(pch=19)으로 그래프에 그림
    
  points(ex8_2$age[ex8_2$sex==2], ex8_2$salary[ex8_2$sex==2], pch=17, col=2)
  # sex가 2인 사람들의 age와 salary 데이터를 빨간색(col=2) 삼각형 점(pch=17)으로 그래프에 그림
    
  legend("bottomright", legend=c("Male","Female"), pch=c(19,17), col=c(4,2))
  # 그래프 오른쪽 하단에 범례를 추가하여 파란색 원(pch=19, col=4)이 Male, 빨간색 삼각형(pch=17, col=2)이 Female을 의미함을 표시

    image.png

R 알기

R 기여자

  • S language 개발
    • John Chambers, Richard Becker, Allan Wilks 등
    • Bell Laboratories (formerly AT&T, now Lucent Technologies
    • Reference
      • Richard A. Becker, John M. Chambers, and Allan R. Wilks. The NewS Language. Chapman & Hall, London, 1988.
  • R 초기 개발자
    • Robert Gentleman and Ross Ihaka
      • Statistics Department of the University of Auckland

image.png

R 매뉴얼

  • An Introduction to R

    image.png

    image.png

R Books

image.png

R Commander

1

library(Rcmdr)

image.png

R Studio

  • R Studio
    • 사용자가 친숙하게 R을 쉽게 사용할 수 있도록 개발된 통합 환경 시스템
  • 다운로드

    image.png

    image.png



연습 문제

  1. 다음 R 명령 수행 결과는?

    1
2

     sq.value <- (function(x) { x*x })
 sq.value(2)

    a. 4

  2. 다음 R 명령 수행 결과는?

    1
2
3
4
5
6
7
8
9
10

     power.value <- function(x,n1,n2,n3=5)
 {  n1.val = x^n1
    n2.val = x^n2
    n3.val = x^n3
    value = list(v1=n1.val, v2=n2.val, v3=n3.val)
    return(value)
 }
    
 aval = powr.value(2, 1/2, 2)
 aval$v1

    a. 1.414

  3. 다음 R 명령 수행 결과는?

    1
2
3
4
5
6
7
8
9
10

     power.value <- function(x,n1,n2,n3=5)
 {  n1.val = x^n1
    n2.val = x^n2
    n3.val = x^n3
    value = list(v1=n1.val, v2=n2.val, v3=n3.val)
    return(value)
 }
    
 aval = powr.value(2, 1/2, 2)
 aval$v3

    a. 32

  4. 상자 그림을 그리는 명령은?

    a. boxplot(ex.data)

Knou, 데이터 정보 처리 입문
knou data information processing
Recently Updated
Contents

[유비쿼터스 컴퓨팅 개론] 13강 - 스마트 자동차

[데이터베이스 시스템] 14강 - 동시성 제어